Hilbert 变换提取信号特征的 Python 实现

\hat{s}(t) ,则有: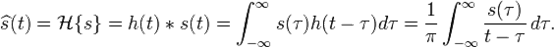
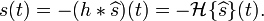
s(t),我们首先把它做一次希尔伯特变换,然后提取特征值。(A-t)间的函数关系。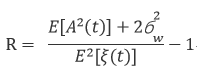

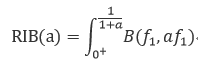
http://xueshu.baidu.com/usercenter/paper/show?paperid=f2c7b987bd3af320909da0e1c09a723b&site=xueshu_se,这篇论文,三种特征值能够很好的表现信号性能。import numpy as np
from math import pi
import matplotlib.pyplot as plt
import math
from scipy import fftpack
from sklearn import preprocessing
import neurolab as nl
#码元数
size = 10
sampling_t = 0.01
t = np.arange(0, size, sampling_t)
#随机生成信号序列
a = np.random.randint(0, 2, size) #产生随机整数序列
m = np.zeros(len(t), dtype=np.float32) #产生一个给定形状和类型的用0填充的数组
for i in range(len(t)):
m[i] = a[int(math.floor(t[i]))]
ts1 = np.arange(0, (np.int64(1/sampling_t) * size))/(10*(m+1))
fsk = np.cos(np.dot(2 * pi, ts1) + pi / 4)
def awgn(y, snr): #snr为信噪比dB值
snr = 10 ** (snr / 10.0)
xpower = np.sum(y ** 2) / len(y)
npower = xpower / snr
return np.random.randn(len(y)) * np.sqrt(npower) + y
def feature_rj(y): #[feature1, f2, f3] = rj(noise_bpsk, fs)
h = fftpack.hilbert(y) # hilbert变换
z = np.sqrt(y**2 + h**2) # 包络
m2 = np.mean(z**2) # 包络的二阶矩
m4 = np.mean(z**4) # 包络的四阶矩
r = abs((m4-m2**2)/m2**2)
Ps = np.mean(y**2)/2
j = abs((m4-2*m2**2)/(4*Ps**2))
return (r,j)
def feature_Bispectrum(y):
ly = size # 行数10
nrecs = np.int64(1 / sampling_t) # 列数100
nlag = 20
nsamp = nrecs # 每段样本数100
nrecord = size
nfft = 128
Bspec = np.zeros((nfft, nfft), dtype=np.float32)
y = y.reshape(ly, nrecs)
c3 = np.zeros((nlag + 1, nlag + 1), dtype=np.float32)
ind = np.arange(nsamp)
for k in range(nrecord):
x = y[k][ind]
x = x - np.mean(x)
for j in range(nlag + 1):
z = np.multiply(x[np.arange(nsamp - j)], x[np.arange(j, nsamp)])
for i in range(j, nlag + 1):
sum = np.mat(z[np.arange(nsamp - i)]) * np.mat(x[np.arange(i, nsamp)]).T
sum = sum / nsamp
c3[i][j] = c3[i][j] + sum # i,j顺序
c3 = c3 / nrecord
c3 = c3 + np.mat(np.tril(c3, -1)).T # 取对角线以下三角,c3为矩阵
c31 = c3[1:, 1:]
c32 = np.mat(np.zeros((nlag, nlag), dtype=np.float32))
c33 = np.mat(np.zeros((nlag, nlag), dtype=np.float32)) # 不可以直接3者相等
c34 = np.mat(np.zeros((nlag, nlag), dtype=np.float32))
for i in range(nlag):
x = c31[i:, i]
c32[nlag - 1 - i, 0:nlag - i] = x.T
c34[0:nlag - i, nlag - 1 - i] = x
if i < (nlag - 1):
x = np.flipud(x[1:, 0]) # 上下翻转,翻转后依然为矩阵
c33 = c33 + np.diag(np.array(x)[:, 0], i + 1) + np.diag(np.array(x)[:, 0], -(i + 1))
c33 = c33 + np.diag(np.array(c3)[0, :0:-1])
cmat = np.vstack((np.hstack((c33, c32, np.zeros((nlag, 1), dtype=np.float32))),
np.hstack((np.vstack((c34, np.zeros((1, nlag), dtype=np.float32))), c3)))) #41*41
Bspec = fftpack.fft2(cmat, [nfft, nfft])
Bspec = np.fft.fftshift(Bspec) #128*128
waxis = np.arange(-nfft / 2, nfft / 2) / nfft
X, Y = np.meshgrid(waxis, waxis)
plt.contourf(X, Y, abs(Bspec),alpha=0,cmap=plt.cm.hot)
plt.contour(X, Y, abs(Bspec))
plt.show()
return Bspec
def features(s):
# for mc in range(2):
snr = np.random.uniform(0, 20) #从一个均匀分布集合中随机采样,左闭右开--[low,high)
s = awgn(s,snr) #在原始信号的基础上增加SNR信噪比的噪音
rj = np.array(feature_rj(s)) #计算R,J特征
z = feature_Bispectrum(s) #计算双谱特征,并画图像
xx = np.int64(np.sqrt(np.size(z))/2)
z = np.array(z[:xx,xx:])
z = np.tril(z).real #取复数z的实部
bis = np.zeros((1, xx),dtype=np.float32) #零组
for i in range(xx):
for j in range(xx-i):
bis[0][i] = bis[0][i]+z[xx-1-j][i+j]
m = bis[0].reshape(1,xx)
normalized = preprocessing.normalize(m)[0,:] #样本各个特征值除以各个特征值的平方之和
features = np.hstack((rj,normalized)) #合并数组r,j和normalized
return features
print(features(fsk))
A,角频率\omega ,初始频率S的改变来说明问题。初始信号图像如下: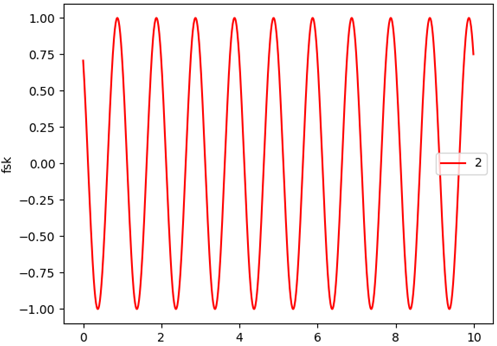
A,\omega ,S从0到2\Pi 均匀变化,对于振幅A的变化,补充代码计算R,J特征值,画出双谱图:R = []
J = []
ts1 = np.arange(0, (np.int64(1/sampling_t) * size))/(10*(m+1))
W = []
Z = []
for i in range(0,40,1):
W.append(i / (2 * pi))
for a1 in W:
global r,j
fsk = a1 * np.cos(np.dot(2 * pi, ts1) + pi / 4)
features(fsk)
R.append(r)
J.append(j)
plt.plot(W, R, color='green', label='1')
plt.legend() # 显示图例
plt.xlabel('A[0-2 * pi]')
plt.ylabel('R')
plt.show()
plt.plot(W, J, color='red', label='2')
plt.legend() # 显示图例
plt.xlabel('A[0-2 * pi]')
plt.ylabel('J')
plt.show()
plt.plot(W, Z, color='red', label='3')
plt.legend() # 显示图例
plt.xlabel('A[0-2 * pi]')
plt.ylabel('trend')
plt.show()
R特征值变化图像: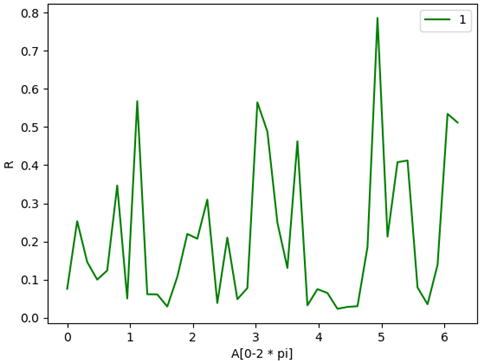
J特征值变化图像: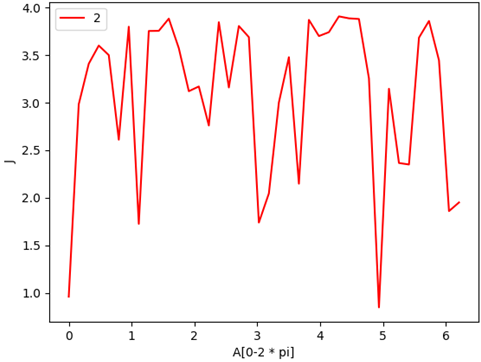
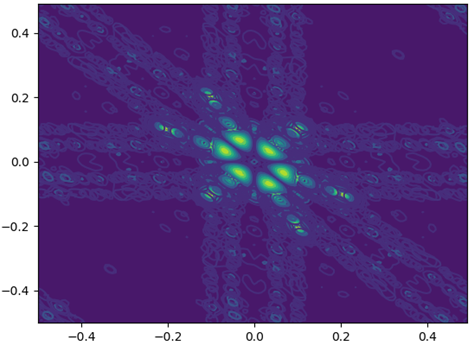
ω的变化,补充代码计算R,J特征值,画出R、J、双谱图像:R = []
J = []
ts1 = np.arange(0, (np.int64(1/sampling_t) * size))/(10*(m+1))
W = []
Z = []
for i in range(0,40,1):
W.append(i / (2 * pi))
for w in W:
global r,j
fsk = np.cos(np.dot(w, ts1) + pi / 4)
features(fsk)
R.append(r)
J.append(j)
plt.plot(W, R, color='green', label='1')
plt.legend() # 显示图例
plt.xlabel('w[0-2 * pi]')
plt.ylabel('R')
plt.show()
plt.plot(W, J, color='red', label='2')
plt.legend() # 显示图例
plt.xlabel('w[0-2 * pi]')
plt.ylabel('J')
plt.show()
plt.plot(W, Z, color='red', label='3')
plt.legend() # 显示图例
plt.xlabel('A[0-2 * pi]')
plt.ylabel('trend')
plt.show()
R特征值变化图像: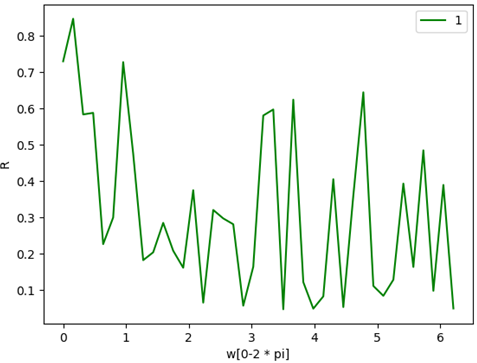
J特征值变化图像:
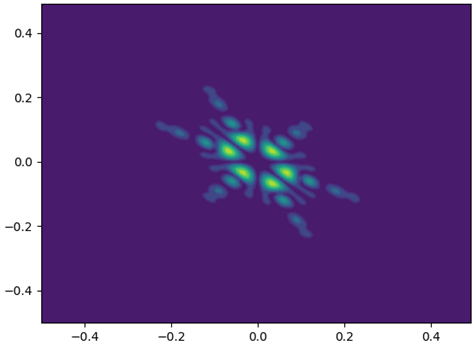
S的变化,补充代码计算R,J特征值,画出双谱图:R = []
J = []
ts1 = np.arange(0, (np.int64(1/sampling_t) * size))/(10*(m+1))
W = []
Z = []
for i in range(0,40,1):
W.append(i / (2 * pi))
for s in W:
global r,j
fsk = np.cos(np.dot(2 * pi, ts1) + s)
features(fsk)
R.append(r)
J.append(j)
plt.plot(W, R, color='green', label='1')
plt.legend() # 显示图例
plt.xlabel('s[0-2 * pi]')
plt.ylabel('R')
plt.show()
plt.plot(W, J, color='red', label='2')
plt.legend() # 显示图例
plt.xlabel('s[0-2 * pi]')
plt.ylabel('J')
plt.show()
plt.plot(W, Z, color='red', label='3')
plt.legend() # 显示图例
plt.xlabel('A[0-2 * pi]')
plt.ylabel('trend')
plt.show()
R特征值变化图像: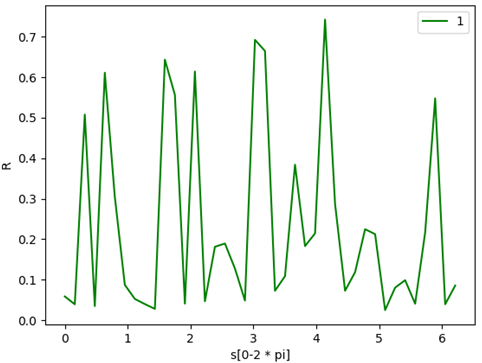
J特征值变化图像: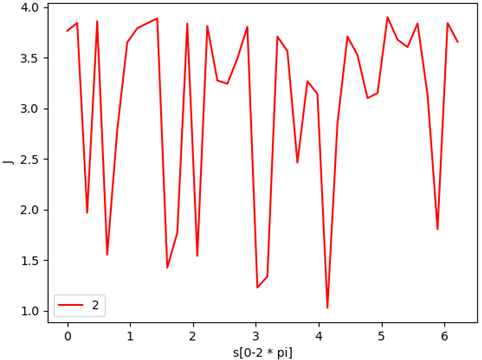

Bspec = fftpack.fft2(cmat, [nfft, nfft])
Bspec = np.fft.fftshift(Bspec) #128*128
waxis = np.arange(-nfft / 2, nfft / 2) / nfft
X, Y = np.meshgrid(waxis, waxis)
plt.contourf(X, Y, abs(Bspec))
plt.contour(X, Y, abs(Bspec))
Z.append(np.mean(abs(Bspec)))
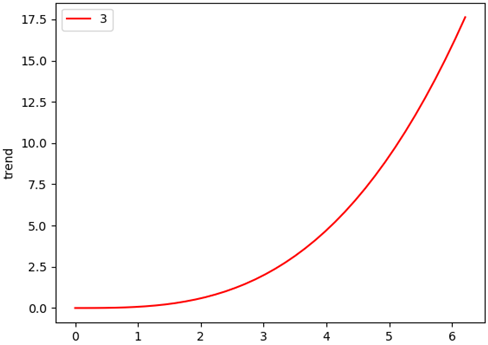
\omega 的双谱特征变化情况: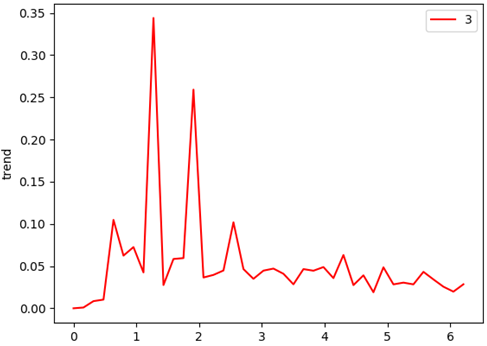
S的双谱特征变化情况: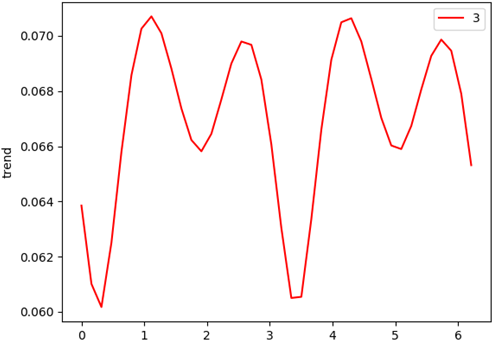
https://github.com/wangwei39120157028/Signal_Feature_Extraction/https://gitee.com/wwy2018/Signal_Feature_Extractionhttps://github.com/wangwei39120157028/IDAPythonScriptshttps://gitee.com/wwy2018/IDAPythonScripts更多阅读
特别推荐

点击下方阅读原文加入社区会员
评论
