从零实现深度学习框架(十三)动手实现逻辑回归

横屏观看,效果更佳!更多文章请关注公众号!
引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
上篇文章对逻辑回归进行了简单的介绍,本文我们就来从零实现逻辑回归。
实现Sigmoid函数
首先实现逻辑回归中的逻辑函数。
def sigmoid(x: Tensor) -> Tensor:
return 1 / (1 + (-x).exp())
正如使用PyTorch一样,我们也只需要实现前向传播。
实现交叉熵损失函数
def binary_cross_entropy(input: Tensor, target: Tensor, reduction: str = "mean") -> Tensor:
errors = -(target * input.log() + (1 - target) * (1 - input).log())
N = len(target)
if reduction == "mean":
loss = errors.sum() / N
elif reduction == "sum":
loss = errors.sum()
else:
loss = errors
return loss
这里的input是经过Sigmoid函数的输出,target是真实输出。我们先定义这样一个方法。然后再实现损失类:
class BCELoss(_Loss):
def __init__(self, reduction: str = "mean") -> None:
super().__init__(reduction)
def forward(self, input: Tensor, target: Tensor) -> Tensor:
return F.binary_cross_entropy(input, target, self.reduction)
实现逻辑回归
有了激活函数、损失函数。我们就可以来实现逻辑回归了。
class LogisticRegression(Module):
def __init__(self, input_dim, output_dim):
self.linear = Linear(input_dim, output_dim)
def forward(self, x: Tensor) -> Tensor:
return F.sigmoid(self.linear(x))
代码非常简单,首先是一个线性回归,然后经过sigmoid即可。有了自动求导工具,我们不必操心反向传播。
下面通过一个实例来应用我们实现的逻辑回归。
学院录取预测
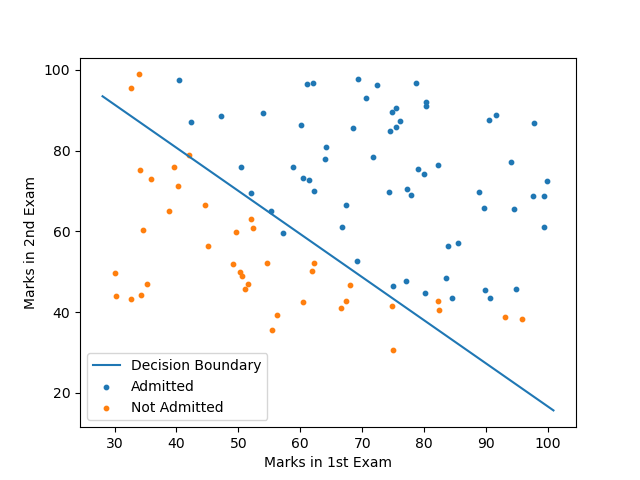
数据集来自吴恩达老师的课程,横坐标表示第一次考试的成绩,纵坐标表示第二次考试的成绩。蓝点表示被学院录取,橙点表示没有被录取。如下图所示:

我们要从中间画一根线,代表决策边界。在下方的样本点判断为没有被录取,在上方的样本点判断为被学院录取。
首先定义加载数据集的函数:
def load_data(path, draw_picture=False):
data = pd.read_csv(path)
X = data.iloc[:, :-1]
y = data.iloc[:, -1]
y = y[:, np.newaxis]
return Tensor(X), Tensor(y)
然后编写训练过程:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from tqdm import tqdm
import metagrad.functions as F
from metagrad.loss import BCELoss
from metagrad.module import Module, Linear
from metagrad.optim import SGD
from metagrad.tensor import Tensor
if __name__ == '__main__':
X, y = load_data("./data/marks.txt", draw_picture=True)
epochs = 200_000 # 迭代20万次
model = LogisticRegression(2, 1) # 输入有2个维度,输出通过的概率。
optimizer = SGD(model.parameters(), lr=1e-3)
loss = BCELoss()
losses = []
for epoch in tqdm(range(int(epochs))): # 显示进度条
optimizer.zero_grad()
outputs = model(X)
l = loss(outputs, y)
optimizer.zero_grad()
l.backward()
optimizer.step()
if (epoch + 1) % 10000 == 0:
total = 0
correct = 0
total += len(y)
correct += np.sum(outputs.numpy().round() == y.numpy()) # 计算准确率
accuracy = 100 * correct / total
losses.append(l.item())
print(f"Train - Loss: {l.item()}. Accuracy: {accuracy}\n")
5%|▌ | 10024/200000 [00:04<01:23, 2271.00it/s]Train - Loss: 0.5822722315788269. Accuracy: 60.60606060606061
10%|▉ | 19855/200000 [00:08<01:19, 2253.23it/s]Train - Loss: 0.5447849631309509. Accuracy: 65.65656565656566
15%|█▍ | 29889/200000 [00:13<01:15, 2262.13it/s]Train - Loss: 0.5130925178527832. Accuracy: 67.67676767676768
20%|█▉ | 39947/200000 [00:17<01:10, 2271.09it/s]Train - Loss: 0.48615676164627075. Accuracy: 75.75757575757575
25%|██▌ | 50040/200000 [00:22<01:05, 2302.86it/s]Train - Loss: 0.46311360597610474. Accuracy: 78.78787878787878
30%|██▉ | 59910/200000 [00:26<01:00, 2300.01it/s]Train - Loss: 0.44325879216194153. Accuracy: 80.8080808080808
35%|███▍ | 69928/200000 [00:30<01:00, 2150.51it/s]Train - Loss: 0.426025390625. Accuracy: 84.84848484848484
40%|███▉ | 79903/200000 [00:35<00:53, 2227.82it/s]Train - Loss: 0.41095882654190063. Accuracy: 85.85858585858585
45%|████▍ | 89928/200000 [00:39<00:48, 2287.55it/s]Train - Loss: 0.3976950943470001. Accuracy: 88.88888888888889
50%|████▉ | 99961/200000 [00:44<00:44, 2269.85it/s]Train - Loss: 0.38594162464141846. Accuracy: 89.8989898989899
55%|█████▍ | 109821/200000 [00:48<00:40, 2223.05it/s]Train - Loss: 0.3754624128341675. Accuracy: 90.9090909090909
60%|█████▉ | 119952/200000 [00:53<00:34, 2305.71it/s]Train - Loss: 0.3660658299922943. Accuracy: 91.91919191919192
65%|██████▍ | 129877/200000 [00:57<00:30, 2295.31it/s]Train - Loss: 0.35759538412094116. Accuracy: 90.9090909090909
70%|███████ | 140024/200000 [01:01<00:26, 2275.92it/s]Train - Loss: 0.3499223589897156. Accuracy: 90.9090909090909
75%|███████▍ | 149947/200000 [01:06<00:21, 2294.55it/s]Train - Loss: 0.34294024109840393. Accuracy: 91.91919191919192
80%|███████▉ | 159852/200000 [01:10<00:17, 2280.32it/s]Train - Loss: 0.3365602195262909. Accuracy: 91.91919191919192
85%|████████▌ | 170017/200000 [01:14<00:12, 2310.93it/s]Train - Loss: 0.3307078182697296. Accuracy: 91.91919191919192
90%|████████▉ | 179960/200000 [01:19<00:08, 2313.34it/s]Train - Loss: 0.32532015442848206. Accuracy: 91.91919191919192
95%|█████████▍| 189875/200000 [01:23<00:04, 2276.93it/s]Train - Loss: 0.320343941450119. Accuracy: 91.91919191919192
100%|██████████| 200000/200000 [01:27<00:00, 2273.90it/s]
Train - Loss: 0.31573355197906494. Accuracy: 91.91919191919192
由于还没有利用GPU,因此耗时了2分钟左右,后续我们的求导工具也可以支持GPU加速。
最后得到的准确率有91.9%,还行。
最后我们要画出决策边界,由于我们的数据只有两个特征,回顾一下Sigmoid的函数图像。当的取值大于时,就判断为正例,否则判断为负例。

因此,我们可以令,得到决策边界的函数:
把看成自变量,看因变量,就可以绘制出如下的图像:
完整代码
完整代码笔者上传到了程序员最大交友网站上去了,地址: [👉 https://github.com/nlp-greyfoss/metagrad]
最后一句:BUG,走你!


Markdown笔记神器Typora配置Gitee图床
不会真有人觉得聊天机器人难吧(一)
Spring Cloud学习笔记(一)
没有人比我更懂Spring Boot(一)
入门人工智能必备的线性代数基础
1.看到这里了就点个在看支持下吧,你的在看是我创作的动力。
2.关注公众号,每天为您分享原创或精选文章!
3.特殊阶段,带好口罩,做好个人防护。
