微积分是所有学问的基础-轻识

好奇心能在正规教育中幸存下来，简直是一种奇迹。

——阿尔伯特·爱因斯坦

不少人会误解“世界中尽是可微函数”。有时在微积分的书里也可以看到这样的表述。

例如，“股价变动的图像可以微分，所以就可以知道未来股价的上下浮动”，如果你读到这样的表述，千万不可相信。

一般讨论股价会使用概率建立模型。最简单的是使用随机摆动的点，即假设股价是随机摆动的。

根据详细的研究可知，这种点的轨迹在任何时候都是锯齿状的（不可微），和刚才的魏尔斯特拉斯函数相似。即，可以证明在点的随机摆动轨迹中，几乎所有的点处都没有切线。股价变动并不是可以用普通微分去预测的温顺之物。在和概率现象纠缠不休的函数中，会频繁出现不可微函数。

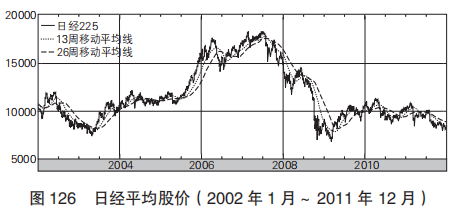
图 126 是日经平均股价的图像。锯齿状的线是实际股价，在顺滑的线中，13 周移动平均线是平均了 13 周的股价，26 周移动平均线同样是平均了过去 26 周的股价。在《股价可以预测》这本书中，恐怕把这条“移动平均线”类的东西作为研究图像了。

移动平均线是低通滤波器（Low Pass Filter）的一种，会移除锯齿状的部分（高频率），只让顺滑的部分（低频率）通过。以声音为例，孩子的声音多是高频率，大叔的声音多是低频率。所以，如果让孩子的声音通过低通滤波器（Low Pass Filter），孩子的声音就会变得像大叔的声音。

在了解股价“大致波动”的时候，因为锯齿状的部分很碍事，所以应该使用移动平均线。

但是，原本的股价“本质上”就是锯齿状的（图 126 的实线）。想要微分这种任何地方都不可微分的内容，不得不说是错误的。

但是，要说股价预测和微积分完全没有关系的话，也并非如此。这种概率模型叫作随机微分方程，使用某种微积分是可以进行解析的。

虽说如此，但这和通常的微积分相当不一样，是一门独特的数学。当然，即使使用随机微分方程式，也无法去预测股价。

微积分的应用虽然不具有预测股价这类功能，但是微积分在现实社会中的作用巨大。可以说， 微积分是所有学问的基础 ，反而很难具体说“微积分在这里起作用”，就像空气和水一样。

微积分的本质在于近似与忽略。 近似指的是忽略一些东西，只给出大概的答案。

即使是复杂的形状，也可以将其视为简单长方形的组合（积分），函数在局部可以视为切线或者抛物线（微分），这个思考角度才是微积分的要领。

重要的是不要在意细节。 不在意细小的部分，“用直线段近似函数图像”就可以搞清楚容积最大的冰激凌蛋卷筒是什么形状，也可以“把曲线看作折线的组合”来计算悬链线的长度。虽然整体计算很难，但分成较小的部分就会变成简单的累加。这就是微积分厉害之处。

实际上，这种思想并不仅限于微积分，可以说整个数学都是这样的。微积分则是了解该方法有效性的最好素材。

实际上，我们居住的现实世界中，近似可以说是无处不在。比如，不存在无限小的东西（无法比基本粒子更小），宇宙也并非无限广阔。

但是，在实际的微积分中，要考虑无限小的量，或者无限大的空间，这是近似。忽略基本粒子的大小，搁置宇宙的边界限制，这种想法或许与事实相悖，但是这种方法给我们带来的恩惠却不可估量。

无须背诵公式、烦琐计算，仅用“阅读”理解微积分原理

丰富图解、亲切解说，传授微积分入门的“巧妙思路”