因果推断的3种偏差

因果关系试图回答的是 what-if 的问题，当且仅当保持其他条件不变，如果改变 X 后，Y 的取值改变，则 X 和 Y 有因果关系，X 导致了 Y。因果关系必然造成相关关系，但是相关关系未必就是因果关系，如果不注意对因果关系和相关关系进行区分，很容易做出错误的判断。

1、两种分析悖论

辛普森悖论

辛普森悖论是指两个变量 X 和 Y 在每个分组中的关系是正（负），但在总体中关系会发生逆转变成负（正）。假设要研究某种药物的疗效，数据里有 30 岁和 40 岁两组人，每组都有服药与未服药的个体，观测数据如下。

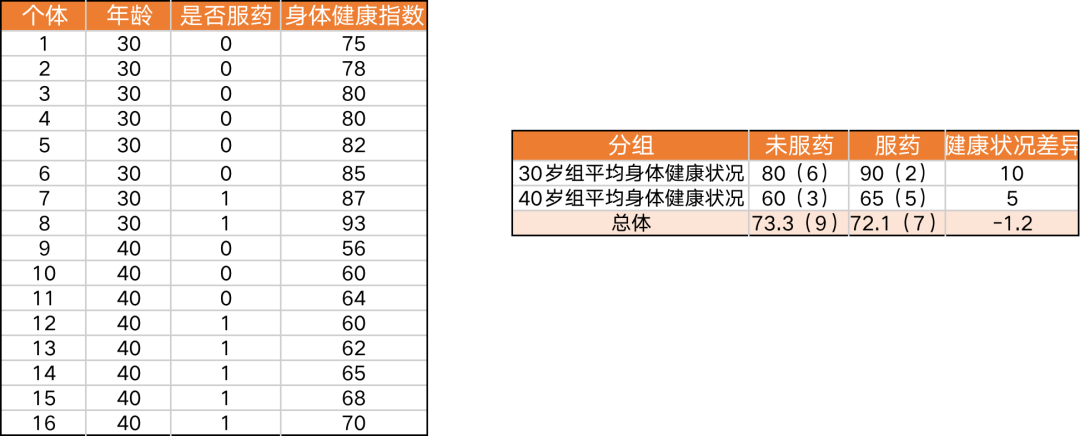
在分组中，服药与健康状况呈正相关，在总体指数中服药与健康指数呈现负相关，为什么总体的结果和分组的结果不一样？哪一种相关性才能反映服药对健康的因果效应？

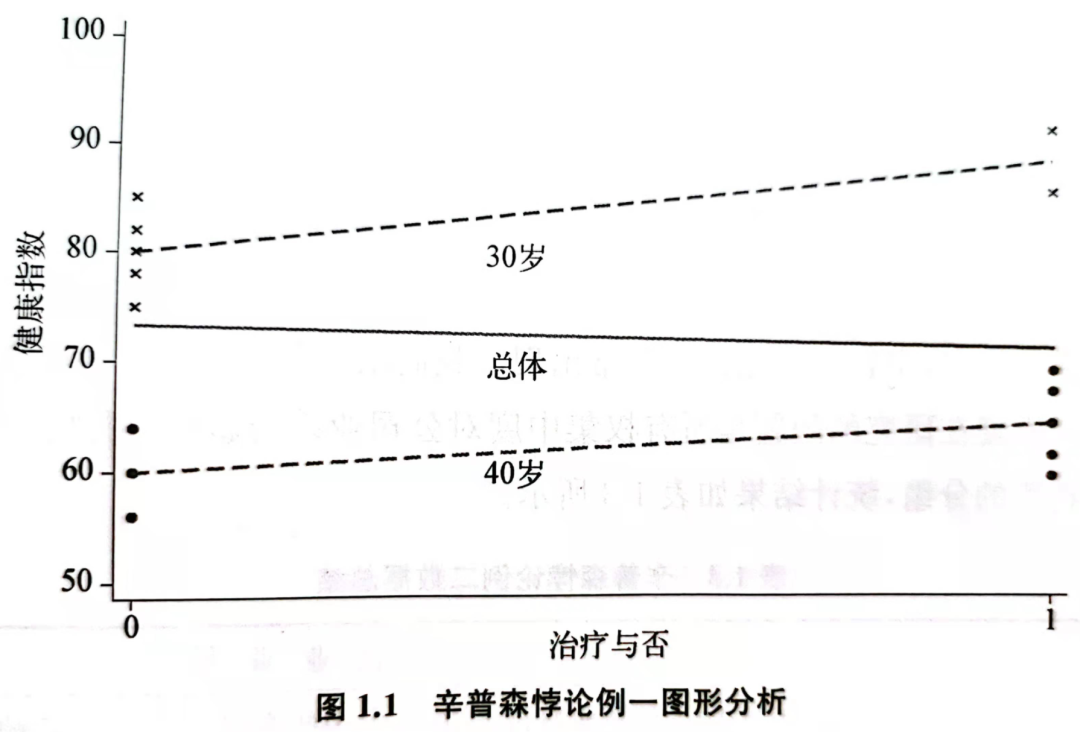从上图可以看出，未服药的人大多数是 30 岁且健康状况较佳的个体，服药者大多数是 40 岁且健康状况较差的个体，因此用总体数据去比较服药者和未服药者的平均状况时，占大多数 30 岁未服药者的健康状况决定了总体未服药的平均健康状况，占大多数 30 岁服药者的健康状况决定了总体服药的平均健康状况，造成总体斜率逆转为负。总体数据的比较结果不完全取决于服药的因果效果，其中还包含年龄因素造成的健康状况差异，总体数据的比较结果未对个体年龄的因素进行控制，造成服药效果中混入个体年龄的影响。

详细案例：人工智能之辛普森悖论：解密撒谎的数据^[1]

伯克森悖论

是指两个本来无关的变量之间体现出貌似强烈的相关关系。伯克森悖论是美国医生和统计学家约瑟夫·伯克森在 1946 年提出的一个命题。他在研究中发现：医院中患有糖尿病的人群中，同时患胆囊炎的人数较少；而没有糖尿病的人群中，患胆囊炎的人数比例则比较高。这似乎可以说明患有糖尿病可以帮助病人减少患胆囊炎的概率，但事实上这个结论是错误的。伯克森悖论的原因是统计样本时，只选择了住院的病人，却忽略了更多的没有住院的样本。正是由于统计数据不够全面，才会导致两个本来无关的变量之间表现出貌似紧密的相关关系。

2、因果关系的三种路径

因果路径（避免过度控制偏差）

因果路径是从解释变量指向被解释变量的路径，其特点是所有箭头指向同一方向，如 X→Z→Y，这种接合形式是被称为“链”接合或中介接合。

一个熟悉的例子是“火灾→烟雾→警报”。虽然我们称这个系统为“火灾警报”，但实际上它应该叫烟雾报警。火灾本身并没有引起警报，所以这里也就没有从火灾直接指向警报的箭头。火灾也不会通过任何其他的变量，比如高温来引发警报，只有火灾向空气中释放的烟雾分子才会触发警报。假如一旦我们知道了烟雾的“值”，关于火的任何新信息便不会再以任何理由让我们增强或削弱对警报的信念，我们就可以说火灾和警报是条件独立的，在这种情况下，中介物Z屏蔽了从X到Y的信息信息，应该避免过度控制。

混淆路径（避免混淆偏差）

混淆路径是指解释变量 X 与被解释变量 Y 之间存在混淆变量的路径，如 X←Z→Y。这种接合形式被称为“叉”接合，Z 通常被视作 X 和 Y 的共因或混杂因子。混杂因子会使X和Y在统计学上发生关联，即使它们之间并没有直接的因果关系。

一个好例子是“鞋的尺码←孩子的年龄→阅读能力”。可以观察到，穿较大码的鞋的孩子往往阅读能力较强，但这种关系是非因果的，给孩子穿大一号的鞋不会让他有更强的阅读能力，相反，这两个变量的变化都可以通过第三个变量，即孩子的年龄来解释。越年长的孩子鞋码越大，他们的阅读能力也越强。我们可以通过“以孩子的年龄为条件”这一操作来消除这种虚假关联。例如，如果我们只看年龄为“七岁”的孩子，我们就会发现这些孩子的鞋码和阅读能力之间没有关系。

对撞路径（避免内生性选择偏差）

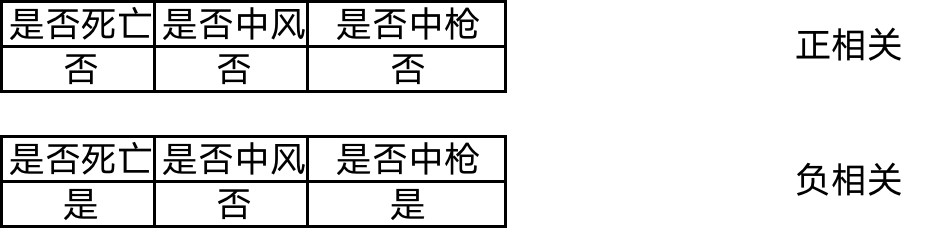
对撞路径是包含对撞变量的路径，对撞变量是被两个变量共同影响的变量，如路径 X→Y←Z。也被称作“对撞”（collider）接合，对撞路径并不会造成两个变量相关，但如果给定了两个变量的对撞变量，会造成两个本不相关的变量之间产生相关关系。

是否中枪和是否中风是没有关系的，但是他们都会决定死亡，如果给定对撞变量是否死亡，就会发现是否中枪和是否中风是相关的。

由于因果关系通常无法被直接观测到，我们只能通过变量间的相关性去推测因果关系，因此从路径的角度看，因果分析的本质就是发现因果路径，截断混淆路径，避免对撞路径产生的衍生路径。

参考资料