宏观视角看递归-轻识

Hi，你好，今天的文章主要是从宏观角度聊聊递归这种算法思想，文章主要内容如下：

通过数组求和看递归的基本性质
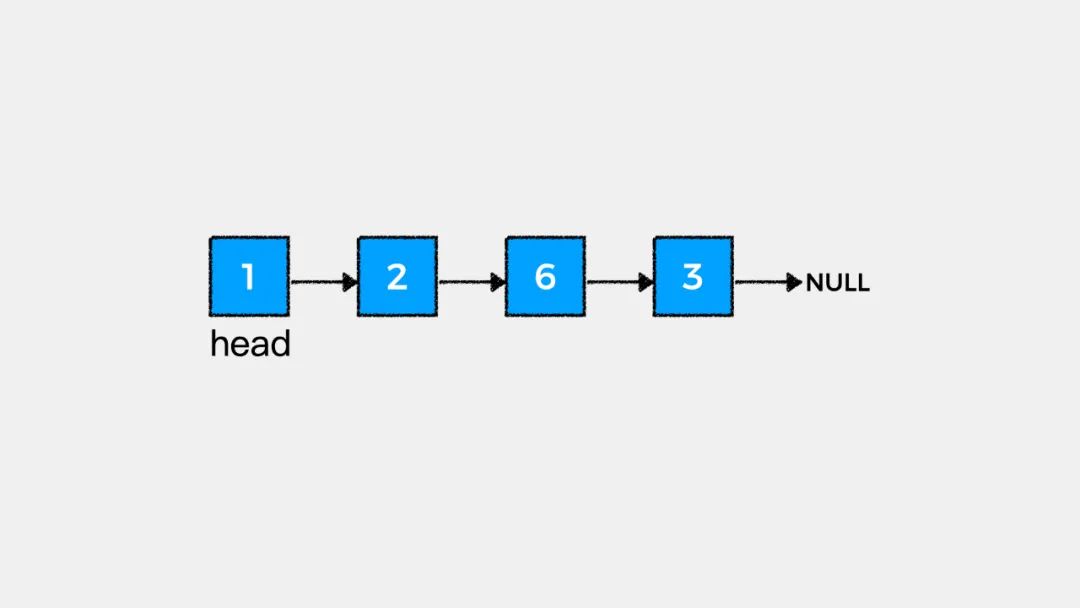
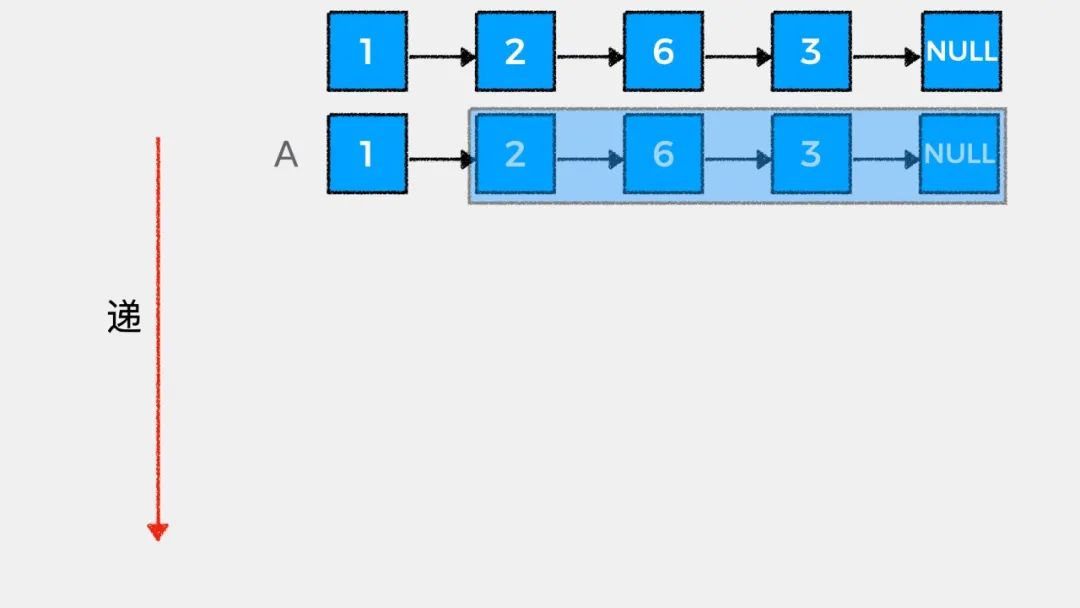
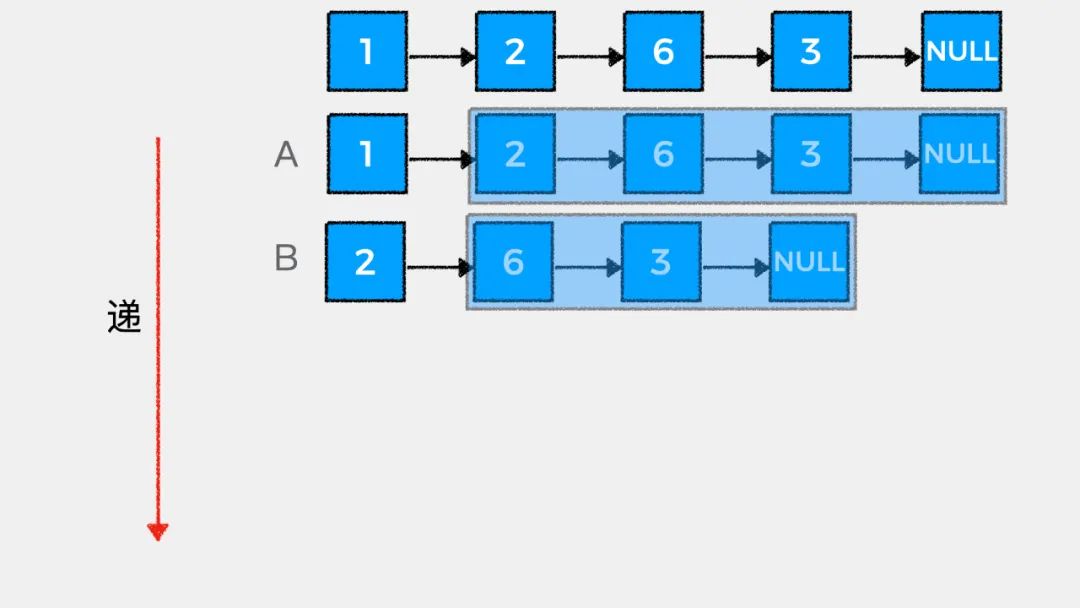
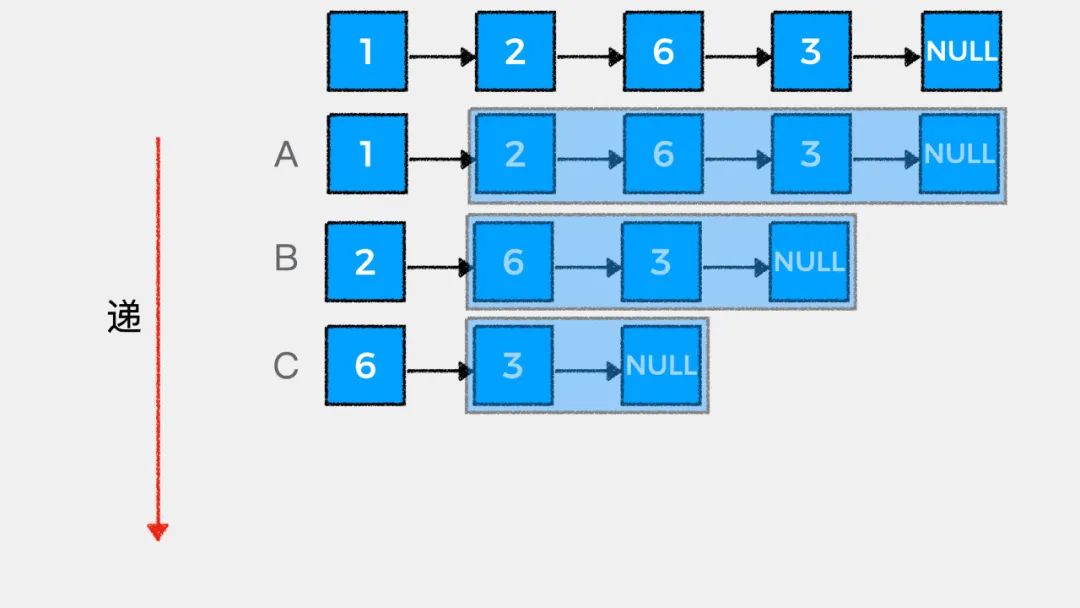
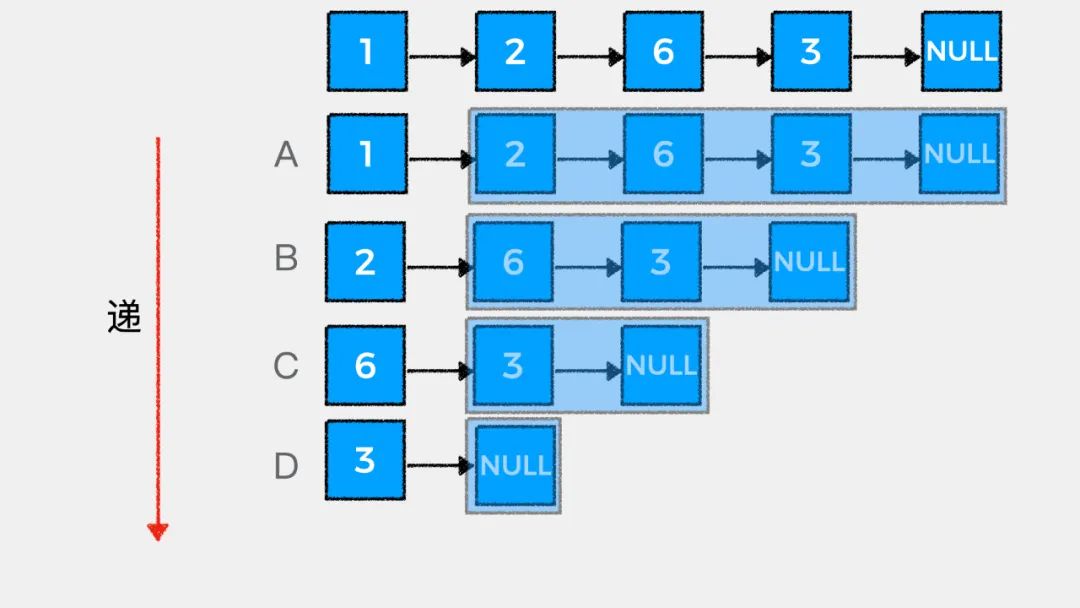
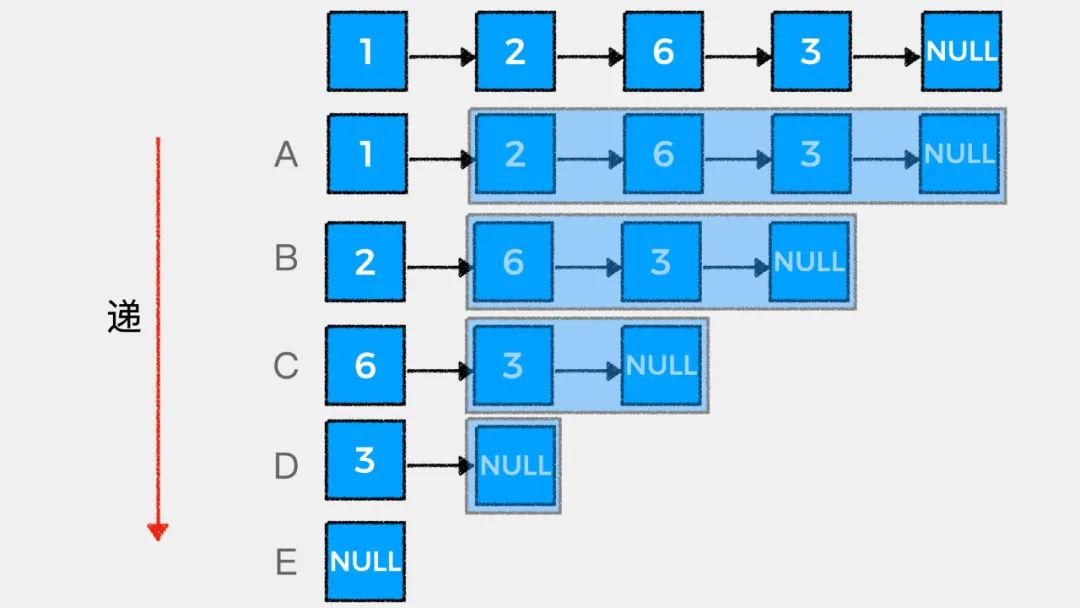
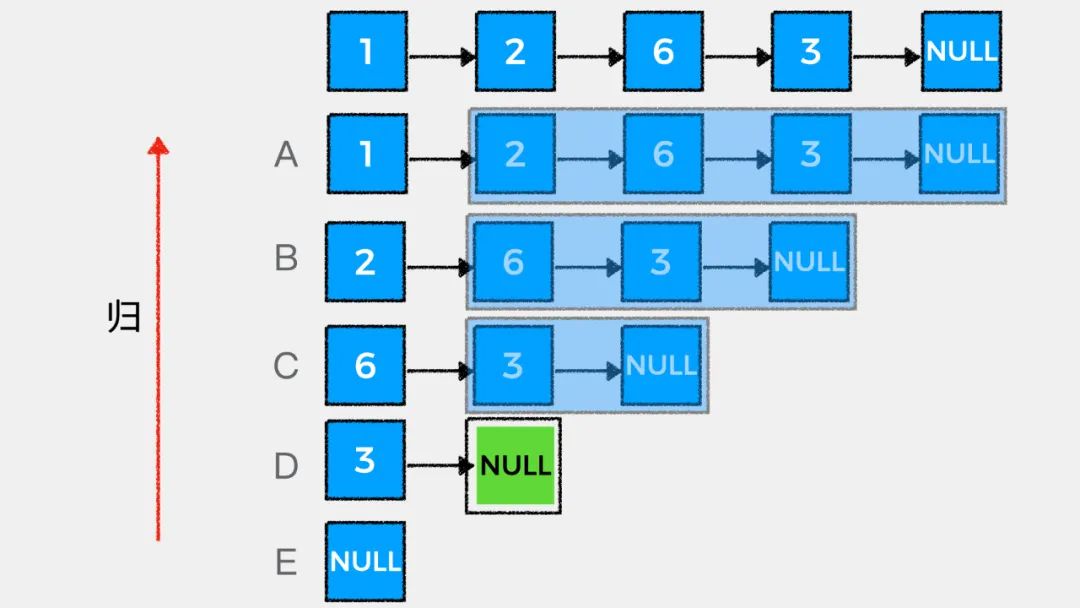
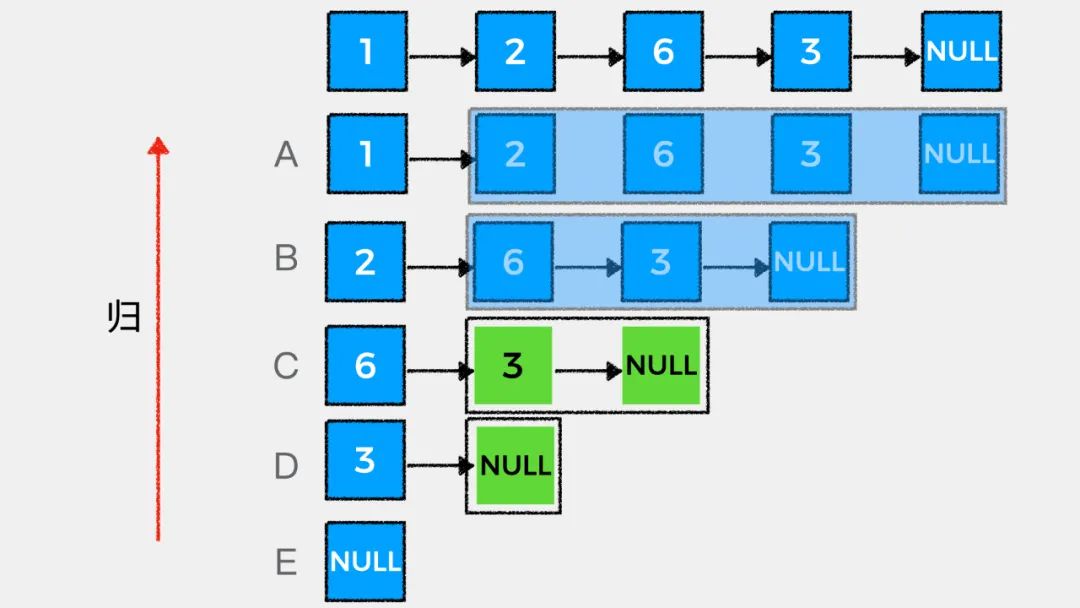
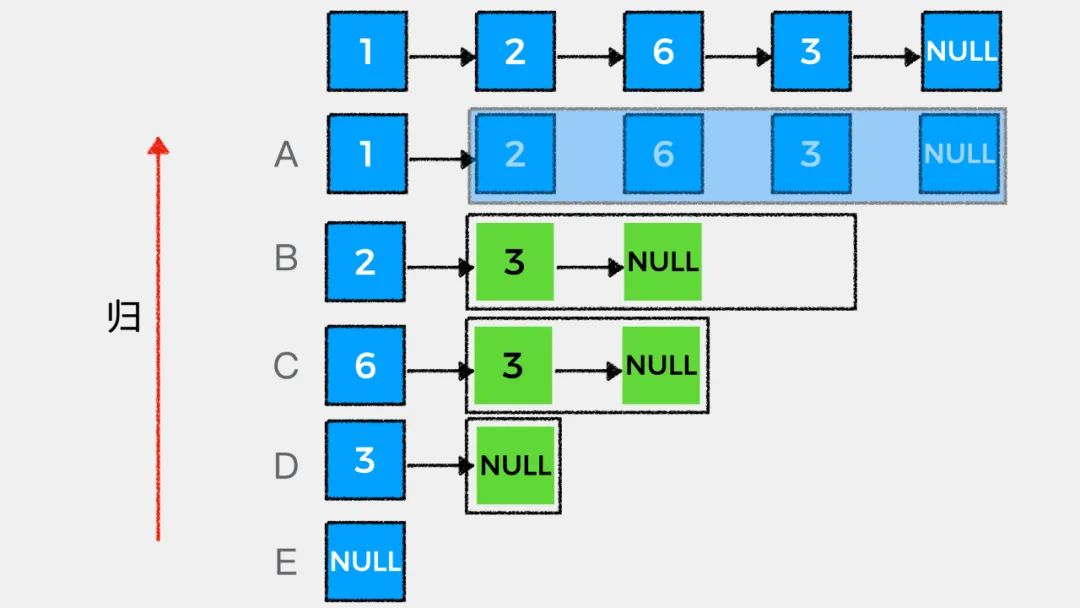
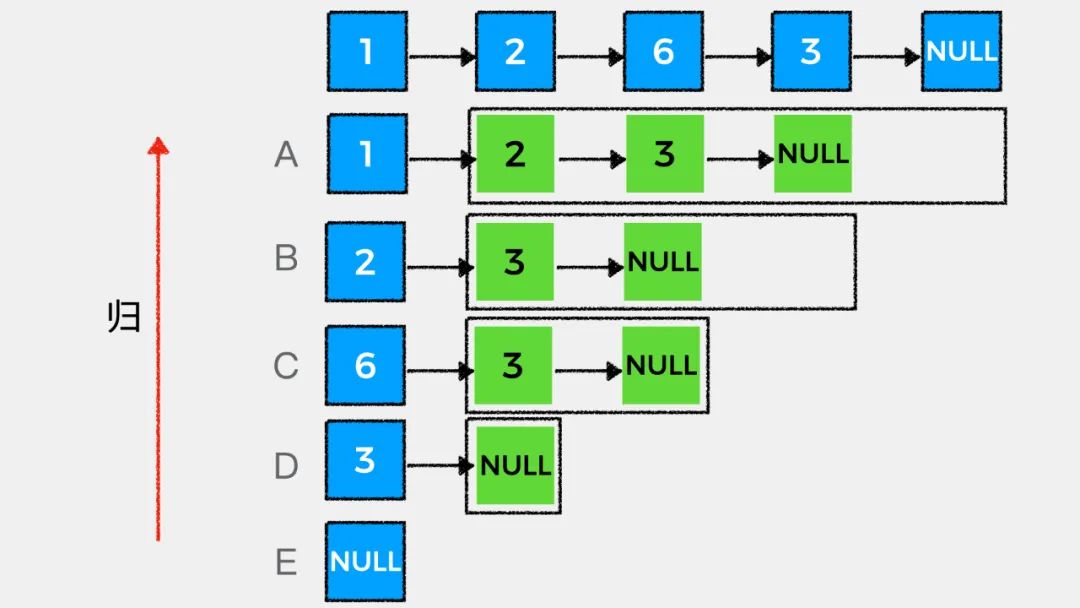
链表的天然递归性

通过数组求和看递归的基本性质

现在给出一个数组arr={1,3,6}，问如何用递归方式求出数组中所有元素的总和。

递归思想介绍

假设现在A拿到了这个问题，但是A只能计算数组中的第一个元素值和剩余元素总和的和，那这时怎么办呢？

A就想，我可以先把数组中第一个元素1的值记录下来，然后让B计算数组中剩余元素的总和。

于是，B就收到一个任务，需要计算数组{3,6}的总和，同样的B和A一样也只能计算数组中的第一个元素值和剩余元素总和的和。因此，B记录下他拿到的数组中的第一个元素3的值，然后让C去计算数组中剩余元素的总和。

这时，C收到一个任务，是计算数组{6}的总和，同样的C和A一样也只能计算数组中的第一个元素值和剩余元素总和的和，并且除了第一个元素外，C不知道数组中还剩余哪些元素。于是，C将数组中的第一个元素6的值记录下来，然后让D去计算数组中剩余元素的总和。

D在收到任务后，一看数组是空的，就知道数组中元素总和是0。

然后D就告诉C，剩余元素的总和是0。于是C将自己记录的元素6和D告诉他的剩余元素的总和0相加后得到6，他就把这个结果告诉了B。

B在收到C的结果6后，同样的将自己记录的元素3和其相加得到9，于是他就把这个结果告诉了A。

A在拿到B告诉他的结果9后，将其和自己记录的元素1相加得到结果10。这时A就知道数组中所有元素的总和是10。

上述过程中A拿到求数组中所有元素和这个问题后，将其告诉B，B再告诉C，C再告诉D，这个过程我们可以称之为”递“。

然后，D将结果告诉C，C再告诉B，B在告诉A的这个过程我们可以称之为”归“。

递归要满足的条件

在上述问题的描述中，其实就包含了递归这种算法思想的一些基本条件：

一是一个问题可以分解为多个更小的子问题并且这多个更小的子问题的求解思路完全一样

对于数组求和这个问题来说，A要知道自己拿到的数组的总和这个问题，可以分解为B要知道除去数组第一个元素外剩余元素总和这样一个问题。

同时，对于A和B来说，他们求解问题的思路是一样的，即只计算自己拿到的数组中第一个元素值和数组中剩余元素总和的和，而不管数组中剩余元素总和的和是如何计算的。

二是存在一个终止条件，可以让递归停下来。

比如数组求和的终止条件就是数组中没有剩余元素需要计算了。

数组求和的递归思路具体如下图：

递归代码的编写

递归代码的编写一是要知道递归终止条件，对于数组求和这个问题来说，其终止条件是数组中没有元素需要计算了，代码表示是：

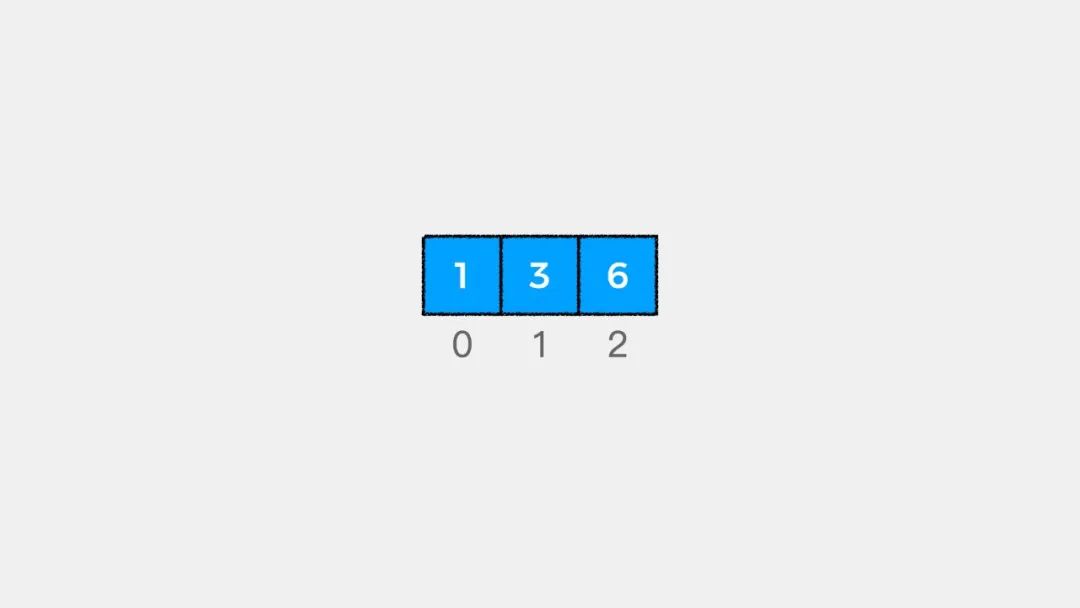
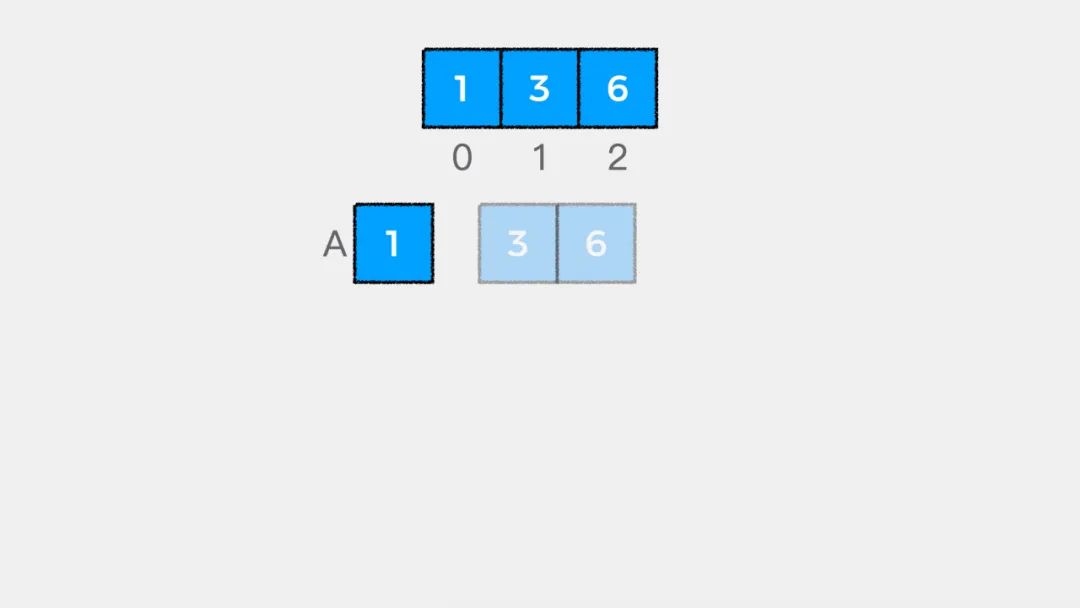
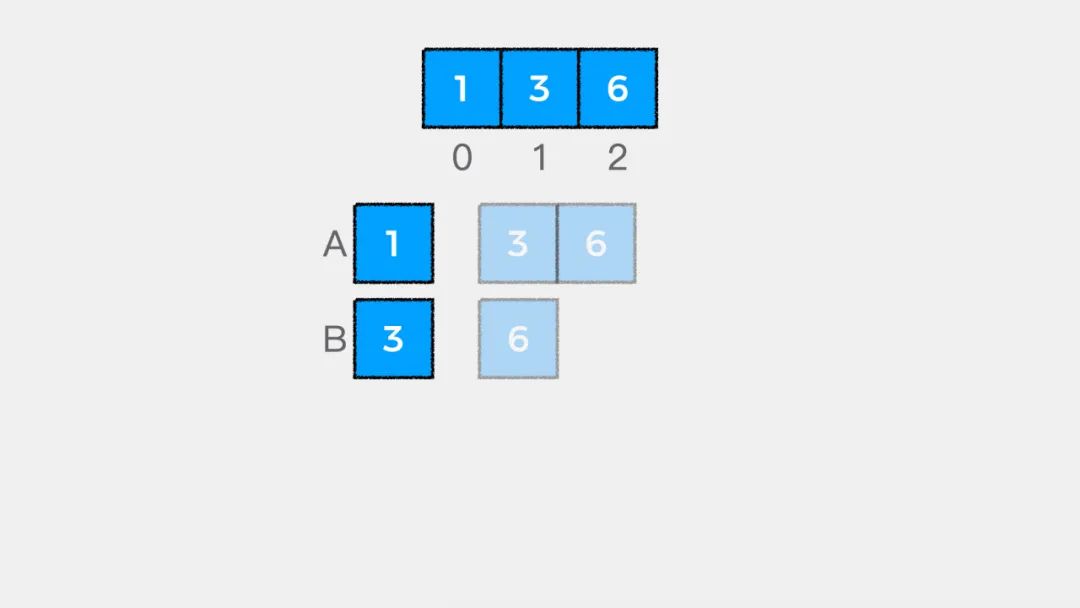
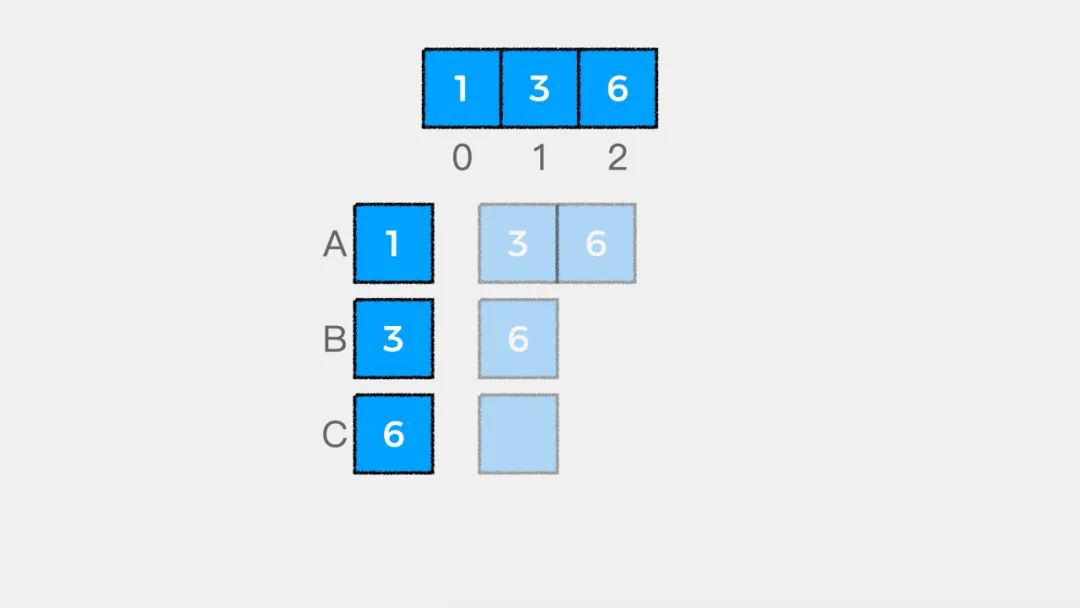
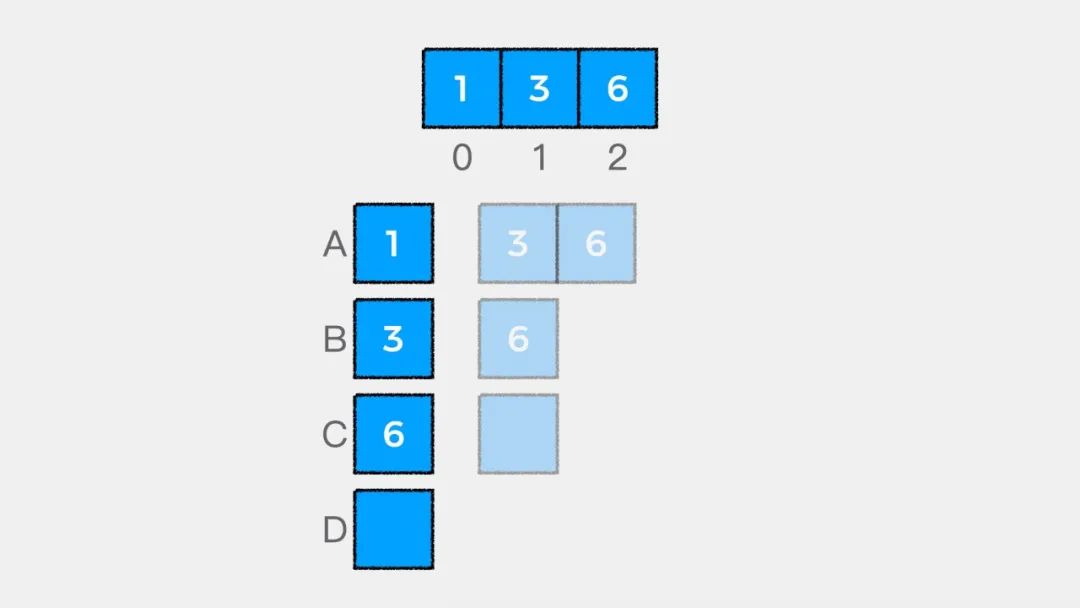
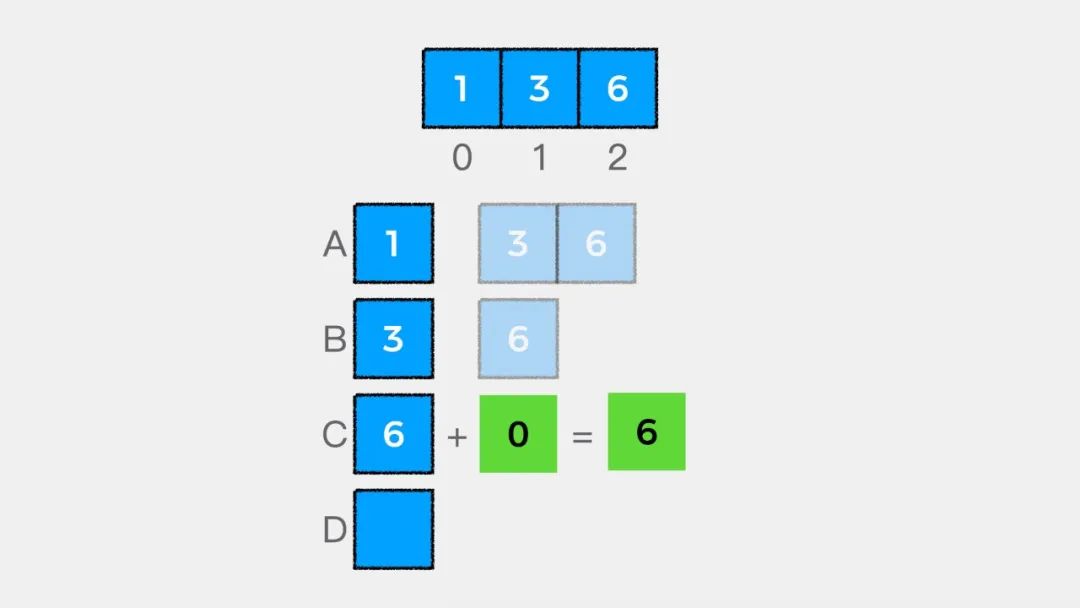
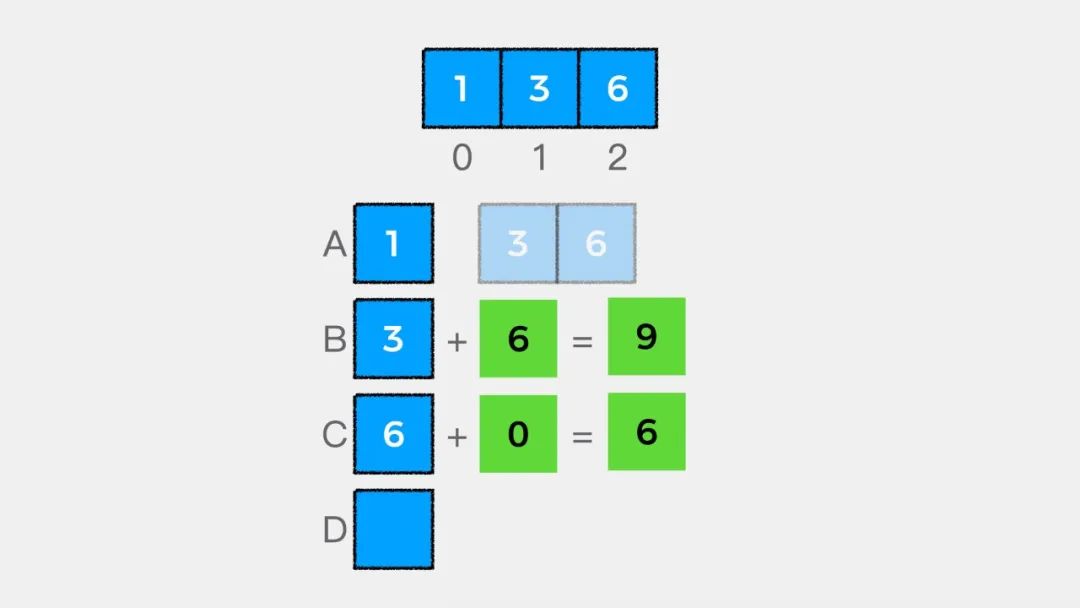
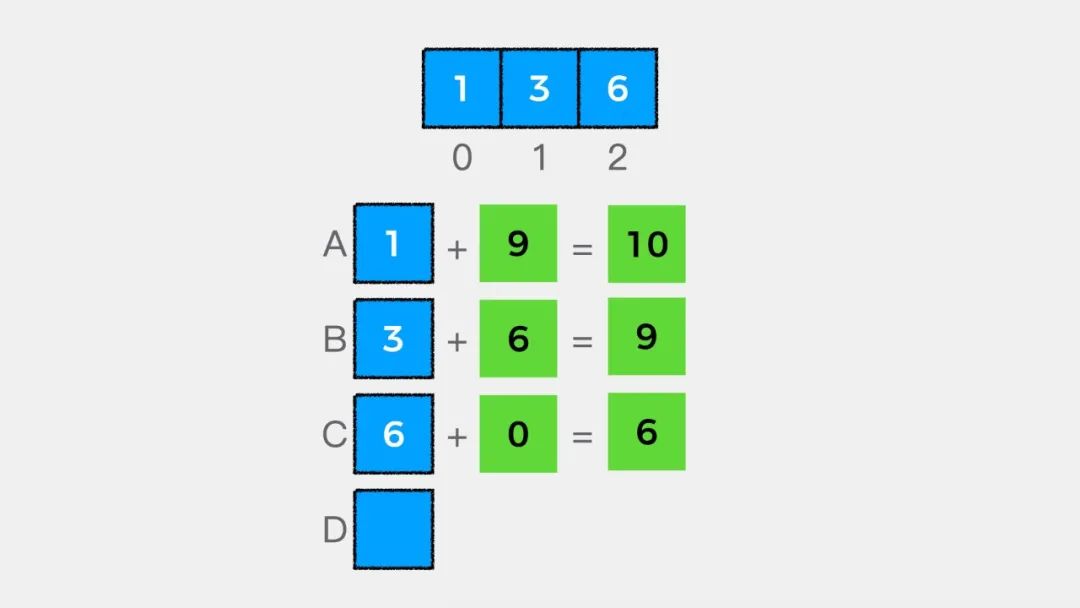
// begin 表示从数组中哪个索引位置开始// 当begin == arr.length表示数组中没有剩余元素if (begin == arr.length) {    return 0;}

二是要知道递归递推公式，就数组求和这个问题来说，递推公式是:

arr[begin] + sum(begin + 1, arr);

有了终止条件和递推公式，就可以写出递归求解数组中所有元素和的代码了，实现如下：

public int sum (int[] arr) {    // 调用递归函数，初始从0开始    return sum(0, arr);}
// 递归函数private int sum(int begin, int[] arr) {    // begin 表示从数组中哪个索引位置开始    // 当begin == arr.length表示数组中没有剩余元素    if (begin == arr.length) {        return 0;    }
    // 我只计算我拿到的数组中第一个元素的值    // 和数组中剩余元素总和的和    return arr[begin] + sum(begin + 1, arr); // 递归调用}

这里我们在第7行sum(int begin, int[] arr)这个方法中调用了sum(int begin, int[] arr)方法它自己，即16行的sum(begin + 1, arr)，这一点可能会让你觉得困惑。

我们可以这样理解，方法sum(int begin, int[] arr)是计算数组中从索引begin开始所有元素的总和，而该方法的计算规则是我计算的是当前数组起始位置begin所对应的元素值和数组中剩余元素的总和的和。那么，我就需要有个方法可以告诉我数组中剩余元素的总和是多少。

这时，刚好有个方法fun(int begin, int[] arr)，只要我告诉它数组是什么样的，以及从哪个索引位置开始计算，它就会告诉我数组中剩余元素的总和。只不过这个方法fun(int begin, int[] arr)所需的参数和我自己一样而已。于是，在代码中看起来就是方法sum(int begin, int[] arr)调用了它自己。

链表的天然递归性

接着我们看下如何用递归思想解答LeetCode中#203.移除链表元素这个问题。

题目描述：
删除链表中等于给定值 val 的所有节点。

示例:
输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5
LeetCode

思路分析

为了方便演示，我将题目示例中给定的链表进行了简化。如下图：

先看下”递“的过程，对于A来说，他在拿到给定的链表后，记录下了头节点，然后将头结点之后的链表给了B。

同样的B在拿到给定的链表后，记录下了头节点，然后将头结点之后的链表给了C。

C在拿到给定的链表后，记录下了头节点，然后将头结点之后的链表给了D。

D在拿到给定的链表后，记录下了头节点，然后将头结点之后的链表给了E。

这时E拿到的链表是一个空链表。

E拿到空链表之后，就将其返回给了D，这时D就知道它的链表是3—>null。

D将自己得到的结果3—>null返回给了C，这时C就知道它的链表是6—>3—>null。

接着C需要将自己计算的结果返回给B，但这时C发现自己拿的链表的头结点是和要移除的元素val=6相等的，因此C返回B的结果应该是去掉头结点6后的剩余部分3—>null。

B在拿到C返回的结果后，就知道它的链表是2—>3—>null。然后，它将这个结果告诉了A。

A在拿到B返回的结果后，就知道它的链表是1—>2—>3—>null，也就是移除链表中元素val=6之后的结果。

对于上述的递归过程，可以简化为两个步骤：

一是记录下链表当前头结点head，然后调用移除链表中结点值val=6的方法；

二是在拿到调用方法之后的结果时，判断一下当前记录的头结点的值是不是等于val=6，如果不等，则将调用方法之后的结果挂在所记录的头结点之后，返回；如果相等，则直接将调用方法之后的结果返回。

链表这种数据结构，我们说它具有天然递归性，就在于对于一个链表，我们可以将其分解为头结点和一个子链表。然后，对于子链表同样可以分解为一个头结点和一个子链表。这满足的是递归思想中的：一个问题可以分解为多个子问题并且这多个子问题求解思路是一样的这一条件。

此外，对于链表分解到最后时，头结点为null，这满足的是递归思想中的：存在递归终止条件，让递归停下来这一条件。

代码实现

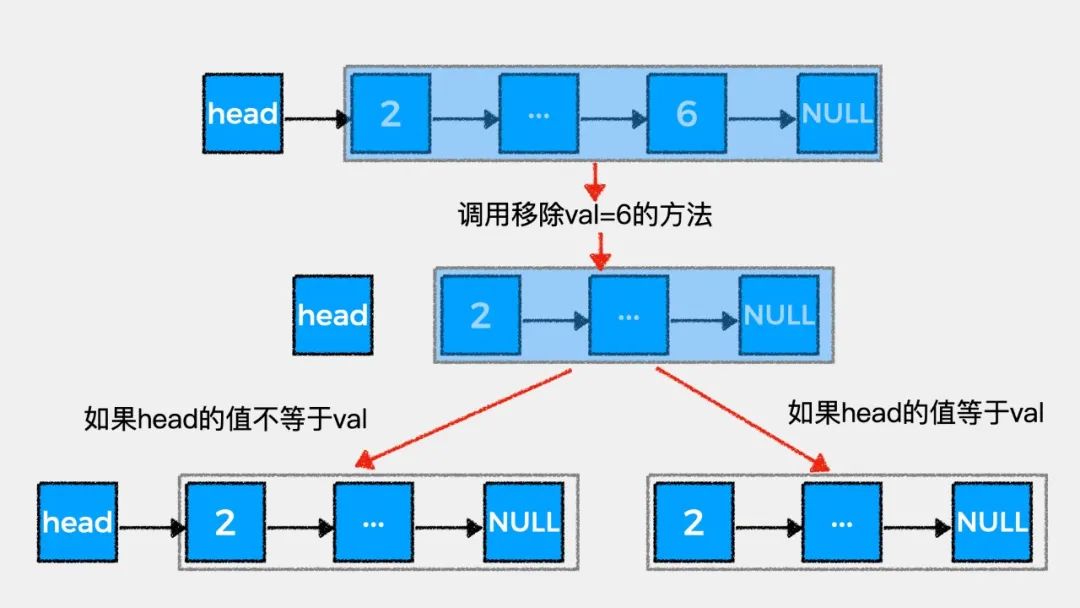
public ListNode removeElements(ListNode head, int val) {    // 递归终止条件    if (head == null) {        return null;    }
    // 调用方法removeElements将当前结点之后的链表部分中的    // 和val值相等的结点删除    ListNode result = removeElements(head.next, val);
    // 如果当前结点head的值等于val则返回result    if (head.val == val) {        return result;    } else {        // 如果当前结点head的值不等于val则        // 将result挂在当前结点head之后返回        head.next = result;        return head;    }}

题图：stux / Pixabay