评估和选择最佳学习模型的一些指标总结

来源:DeepHub IMBA 本文约2700字,建议阅读5分钟
在本文中,我将讨论和解释其中的一些方法,并给出使用 Python 代码的示例。

混淆矩阵
#Import Libraries:
from random import random
from random import randint
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import roc_curve
#Fabricating variables:
#Creating values for FeNO with 3 classes:
FeNO_0 = np.random.normal(15,20, 1000)
FeNO_1 = np.random.normal(35,20, 1000)
FeNO_2 = np.random.normal(65, 20, 1000)
#Creating values for FEV1 with 3 classes:
FEV1_0 = np.random.normal(4.50, 1, 1000)
FEV1_1 = np.random.uniform(3.75, 1.2, 1000)
FEV1_2 = np.random.uniform(2.35, 1.2, 1000)
#Creating values for Bronco Dilation with 3 classes:
BD_0 = np.random.normal(150,49, 1000)
BD_1 = np.random.uniform(250,50,1000)
BD_2 = np.random.uniform(350, 50, 1000)
#Creating labels variable with two classes (1)Disease (0)No disease:
no_disease = np.zeros((1500,), dtype=int)
disease = np.ones((1500,), dtype=int)
#Concatenate classes into one variable:
FeNO = np.concatenate([FeNO_0, FeNO_1, FeNO_2])
FEV1 = np.concatenate([FEV1_0, FEV1_1, FEV1_2])
BD = np.concatenate([BD_0, BD_1, BD_2])
dx = np.concatenate([not_asma, asma])
#Create DataFrame:
df = pd.DataFrame()#Add variables to DataFrame:
df['FeNO'] = FeNO.tolist()
df['FEV1'] = FEV1.tolist()
df['BD'] = BD.tolist()
df['dx'] = dx.tolist()
#Create X and y:
X = df.drop('dx', axis=1)
y = df['dx']#Train and Test split:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
#Build the model:
logisticregression = LogisticRegression().fit(X_train, y_train)
#Print accuracy metrics:
print("training set score: %f" % logisticregression.score(X_train, y_train))
print("test set score: %f" % logisticregression.score(X_test, y_test))

# Predicting labels from X_test data
y_pred = logisticregression.predict(X_test)
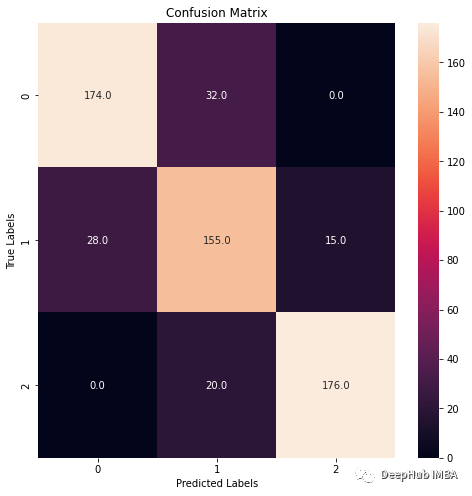
# Create the confusion matrix
confmx = confusion_matrix(y_test, y_pred)
f, ax = plt.subplots(figsize = (8,8))
sns.heatmap(confmx, annot=True, fmt='.1f', ax = ax)
plt.xlabel('Predicted Labels')
plt.ylabel('True Labels')
plt.title('Confusion Matrix')
plt.show();

#Fabricating variables:
#Creating values for FeNO with 3 classes:
FeNO_0 = np.random.normal(15,20, 1000)
FeNO_1 = np.random.normal(35,20, 1000)
FeNO_2 = np.random.normal(65, 20, 1000)
#Creating values for FEV1 with 3 classes:
FEV1_0 = np.random.normal(4.50, 1, 1000)
FEV1_1 = np.random.normal(3.75, 1.2, 1000)
FEV1_2 = np.random.normal(2.35, 1.2, 1000)
#Creating values for Broncho Dilation with 3 classes:
BD_0 = np.random.normal(150,49, 1000)
BD_1 = np.random.normal(250,50,1000)
BD_2 = np.random.normal(350, 50, 1000)
#Creating labels variable with three classes:
no_disease = np.zeros((1000,), dtype=int)
possible_disease = np.ones((1000,), dtype=int)
disease = np.full((1000,), 2, dtype=int)
#Concatenate classes into one variable:
FeNO = np.concatenate([FeNO_0, FeNO_1, FeNO_2])
FEV1 = np.concatenate([FEV1_0, FEV1_1, FEV1_2])
BD = np.concatenate([BD_0, BD_1, BD_2])
dx = np.concatenate([no_disease, possible_disease, disease])
#Create DataFrame:
df = pd.DataFrame()
#Add variables to DataFrame:
df['FeNO'] = FeNO.tolist()
df['FEV1'] = FEV1.tolist()
df['BD'] = BD.tolist()
df['dx'] = dx.tolist()
#Creating X and y:
X = df.drop('dx', axis=1)
y = df['dx']#Data split into train and test:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)#Fit Logistic Regression model:
logisticregression = LogisticRegression().fit(X_train, y_train)
#Evaluate Logistic Regression model:
print("training set score: %f" % logisticregression.score(X_train, y_train))
print("test set score: %f" % logisticregression.score(X_test, y_test))

# Predicting labels from X_test data
y_pred = logisticregression.predict(X_test)
# Create the confusion matrix
confmx = confusion_matrix(y_test, y_pred)
f, ax = plt.subplots(figsize = (8,8))
sns.heatmap(confmx, annot=True, fmt='.1f', ax = ax)
plt.xlabel('Predicted Labels')
plt.ylabel('True Labels')
plt.title('Confusion Matrix')
plt.show();
评价指标
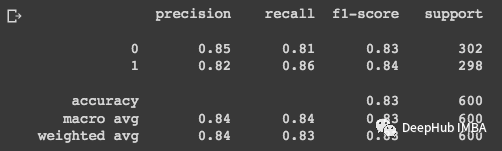
准确性Accuracy:我们的模型在预测结果方面有多好。此指标用于度量模型输出与目标结果的接近程度(所有样本预测正确的比例)。 精度Precision:我们预测的正样本有多少是正确的?查准率(预测为正样本中,有多少实际为正样本,预测的正样本有多少是对的)。 召回Recall:我们的样本中有多少是目标标签?查全率(有多少正样本被预测了,所有正样本中能预测对的有多少)。 F1 Score:是查准率和查全率的加权平均值。
# Printing the model scores:
print(classification_report(y_test, y_pred))
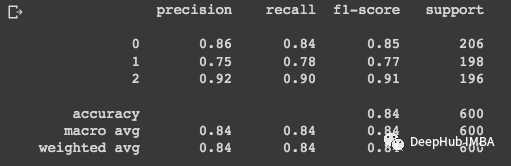
# Printing the model scores:
print(classification_report(y_test, y_pred))
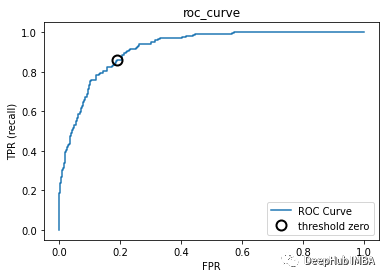
ROC和AUC
#Get the values of FPR and TPR:
fpr, tpr, thresholds = roc_curve(y_test,logisticregression.decision_function(X_test))
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
plt.title("roc_curve");
# find threshold closest to zero:
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
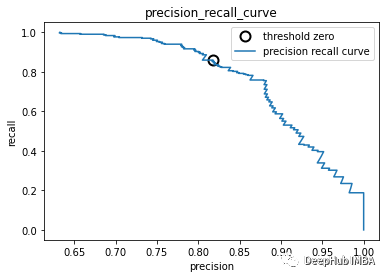
PR(precision recall )曲线
#Get precision and recall thresholds:
precision, recall, thresholds = precision_recall_curve(y_test,logisticregression.decision_function(X_test))
# find threshold closest to zero:
close_zero = np.argmin(np.abs(thresholds))
#Plot curve:
plt.plot(precision[close_zero],
recall[close_zero],
'o',
markersize=10,
label="threshold zero",
fillstyle="none",
c='k',
mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.xlabel("precision")
plt.ylabel("recall")
plt.title("precision_recall_curve");
plt.legend(loc="best")
编辑:王菁
校对:林亦霖
评论
