从L1 loss到EIoU loss,目标检测边框回归的损失函数一览

极市导读
目标检测任务的损失函数由Classificition Loss和BBox Regeression Loss两部分构成。本文介绍目标检测任务中近几年来Bounding Box Regression Loss Function的演进过程。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
目标检测任务的损失函数由Classificition Loss和BBox Regeression Loss两部分构成。本文介绍目标检测任务中近几年来Bounding Box Regression Loss Function的演进过程,其演进路线是 Smooth L1 Loss IoU Loss GIoU Loss DIoU Loss CIoU Loss EIoU Loss,本文按照此路线进行讲解。
L1/L2 Loss
L1/L2 Loss 的定义
此前回归一般采用 Loss,定义如下:
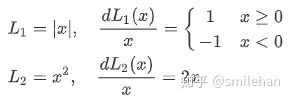
L1/L2 Loss 的缺点
但是这两者存在一些缺点:
L1 Loss 对 x 的导数为常数,由于 x 代表真实值与预测值的差值,故在训练后期,x 很小时,如果学习率不变,损失函数会在稳定值附近波动,难以收敛到更高精度; L2 Loss 在 x 值很大时,其导数非常大,故在训练初期不稳定。
Smooth L1 Loss
Smooth L1 Loss 的定义
针对 Loss 存在的缺点,修正后得到 [1]:
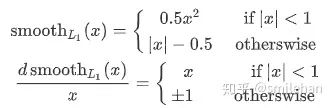
在 x 较小时为 L2 Loss,在 x 较大时为 L1 Loss,扬长避短。应用在目标检测的边框回归中,位置损失如下所示:
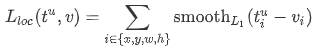
其中 表示 bbox 位置的真实值, 表示 bbox 位置回归的预测值。
Smooth L1 Loss 的缺点
在计算目标检测的 bbox loss时,都是独立的求出4个点的 loss,然后相加得到最终的 bbox loss。这种做法的默认4个点是相互独立的,与实际不符。举个例子,当(x, y)为右下角时,w h其实只能取0; 目标检测的评价 bbox 的指标是 IoU,IoU 与 的变化不匹配。
IoU Loss
IoU Loss 的定义
针对 Loss 的缺点,IoU Loss[2]如下:
实现时甚至简化为:
IoU 计算让 x, y, w, h 相互关联,同时具备了尺度不变性,克服了 Loss 的缺点。
IoU Loss 的缺点
当然 IoU Loss 也并不完美:
当预测框和目标框不相交,即 IoU(bbox1, bbox2)=0 时,不能反映两个框距离的远近,此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。 假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,其 IoU 值是相同时,IoU 值不能反映两个框是如何相交的,如图所示:
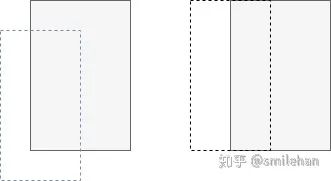
灰色框为真实框,虚线框为预测框。这两者情况的IoU相同,但是这两个框的匹配状态不一样。我们认为右边框匹配的好一点,因为它匹配的角度更好。故下文定义了GIoU。
GIoU Loss
GIoU 的定义
承接上一小节提到的情况,IoU 不能区分一些相交的情况,故论文[3]提出GIoU作为度量指标。
GIoU 的实现方式如上式,其中 C 为 A 和 B 的外接矩形。用 C 减去 A 和 B 的并集除以 C 得到一个数值,然后再用 A 和 B 的 IoU 减去这个数值即可得到 GIoU 的值。可以看出:
GIoU 取值范围为 [-1, 1],在两框重合时取最大值1,在两框无限远的时候取最小值-1; 与 IoU 只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。
GIoU Loss 的定义
定义了 GIoU 之后,按照 IoU Loss 的思路定义 GIoU Loss:
GIoU Loss 的缺点
当目标框完全包裹预测框的时候,IoU 和 GIoU 的值都一样,此时 GIoU 退化为 IoU, 无法区分其相对位置关系。

灰色框为真实框,绿色为预测框,上图三种情况GIoU均相同,但是我们认为中间的预测框应该由于另外两个框。
DIoU Loss
DIoU 的定义
针对 IoU和GIoU 的缺点,论文[4]总结提出了边框回归的三个重要几何因素:重叠面积、中心点距离和长宽比,提出 DIoU和CIoU,本节先介绍 DIoU。
首先,论文[^ 4]总结了 IoU-based loss 的范式:
表示预测框与真实框的惩罚项,将惩罚项设置为:
其中 表示框的中心点, 表示欧氏距离,c 表示最小外接矩形的对角线距离,故 DIoU 如下所示:
DIoU 就是在 IoU 基础上加入中心点归一化距离,所以可以更好地表达两个框的距离。同时,文章利用 DIoU 距离,设计了 DIoU-nms。
DIoU Loss 的定义
根据范式,DIoU Loss:
DIoU Loss 的缺点
边框回归的三个重要几何因素:重叠面积、中心点距离和长宽比,DIoU 没有包含长宽比因素。
CIoU Loss
CIoU 的定义
CIoU[^ 4] 在 DIoU 的基础上,增加了长宽比影响因子 ,合并到惩罚项:
其中 v 用于衡量长宽比的一致性, 用于平衡 v 的值,设为:
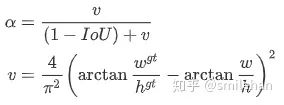
CIoU Loss 的定义
v的导数:
CIoU Loss 的缺点
在CIoU的定义中,衡量长宽比的过于复杂,从两个方面减缓了收敛速度:
长宽比不能取代单独的长宽,比如 都会导致v=0; 从v的导数可以得到 ,这说明 和 在优化中意义相反。
EIoU Loss
EIoU 的定义
论文[5]用 取代 即可。
EIoU Loss的定义
Focal-EIoU Loss的定义
focal loss可以理解为对损失加权,常见的分类focal loss为 。本文首先尝试直接将EIoU带入,但是效果不好,最后得到:
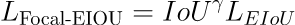
Conclusion
总的来看,我认为目标检测边框回归的损失函数设计应当遵循以下原则:
应该按照边框的物理含义定义边框间的距离,以设计损失函数。从 到 ,对边框间距离的物理描述愈发准确。 注意算法各个模块之间的配合,比如 DIoU 与 DIoU-nms 组合才能达到更好的效果。
参考
^Girshick R. Fast r-cnn[C]//Proceedings of the IEEE international conference on computer vision. 2015: 1440-1448. ^Yu J, Jiang Y, Wang Z, et al. Unitbox: An advanced object detection network[C]//Proceedings of the 24th ACM international conference on Multimedia. 2016: 516-520. ^Rezatofighi H, Tsoi N, Gwak J Y, et al. Generalized intersection over union: A metric and a loss for bounding box regression[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019: 658-666. ^Zheng Z, Wang P, Liu W, et al. Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression[J]. arXiv preprint arXiv:1911.08287, 2019. ^Focal and Efficient IOU Loss for Accurate Bounding Box Regression
推荐阅读

