手把手教你用Python实现查找算法
导读:在复杂的数据结构中高效地查找数据是其非常重要的功能之一。最简单的方法是在每个数据点中查找所需数据,效率并不高。因此随着数据规模的增加,我们需要设计更复杂的算法来查找数据。

线性查找(Linear Search) 二分查找(Binary Search) 插值查找(Interpolation Search)
def LinearSearch(list, item):
index = 0
found = False
# Match the value with each data element
while index < len(list) and found is False:
if list[index] == item:
found = True
else:
index = index + 1
return found
list = [12, 33, 11, 99, 22, 55, 90]
print(LinearSearch(list, 12))
print(LinearSearch(list, 91))
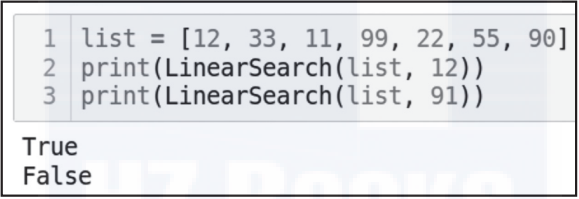
线性查找的性能:如上所述,线性查找是一种执行穷举搜索的简单算法,其最坏时间复杂度是O(N)。
def BinarySearch(list, item):
first = 0
last = len(list)-1
found = False
while first<=last and not found:
midpoint = (first + last)//2
if list[midpoint] == item:
found = True
else:
if item < list[midpoint]:
last = midpoint-1
else:
first = midpoint+1
return found
list = [12, 33, 11, 99, 22, 55, 90]
sorted_list = BubbleSort(list)
print(BinarySearch(list, 12))
print(BinarySearch(list, 91))
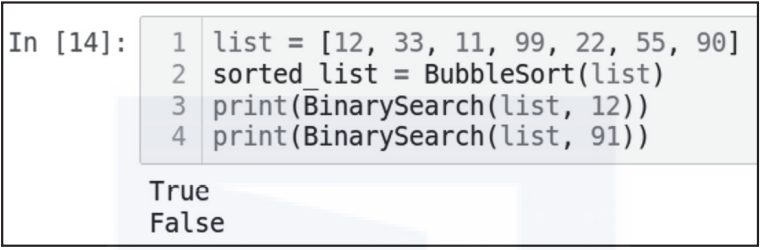
二分查找的性能:二分查找之所以如此命名,是因为在每次迭代中,算法都会将数据分成两部分。如果数据有N项,则它最多需要O(log N)步来完成迭代,这意味着算法的运行时间为O(log N)。
def IntPolsearch(list,x ):
idx0 = 0
idxn = (len(list) - 1)
found = False
while idx0 <= idxn and x >= list[idx0] and x <= list[idxn]:
# Find the mid point
mid = idx0 +int(((float(idxn - idx0)/( list[idxn] - list[idx0])) * ( x - list[idx0])))
# Compare the value at mid point with search value
if list[mid] == x:
found = True
return found
if list[mid] < x:
idx0 = mid + 1
return found
list = [12, 33, 11, 99, 22, 55, 90]
sorted_list = BubbleSort(list)
print(IntPolsearch(list, 12))
print(IntPolsearch(list,91))
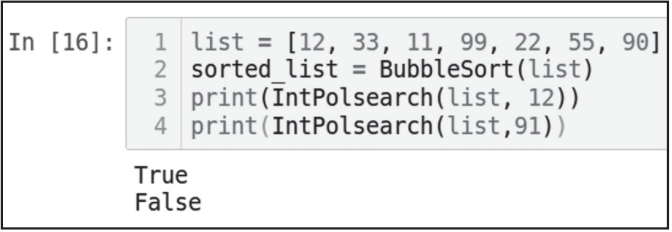
插值查找的性能:如果数据分布不均匀,则插值查找算法的性能会很差,该算法的最坏时间复杂度是O(N)。如果数据分布得相当均匀,则最佳时间复杂度是O(log(log N))。


干货直达👇
评论
