保姆级教学!彻底学会时间复杂度和空间复杂度
大家好呀,我是蛋蛋。
数据结构与算法,作为编程界从入门到劝退的王者,是很多初学者心中神圣而想侵犯的村花儿,化身舔狗,费尽心思,舔到最后,我命油我不油天。

作为一名大学之前编程能力为零,以为计算机专业就是打游戏的咸鱼,到参加 ACM 竞赛,靠着划水和抱大腿拿了几块金银铜铁牌的前 ACM 混子选手,想起之前疯狂跪舔数据结构和算法的日子,至今我扔能掬出一把辛酸泪。

为了让臭宝们不再像我这样当个人这么难,我决定和大家一起学习数据结构与算法,我希望能用傻瓜的方式,由浅入深,从概念到实践,一步一步的来,这个过程可能会很长,我希望在这个过程中你能喜欢上它,能发现它们冰冷外表下有趣的灵魂。
学习数据结构与算法的第一课,我永远都选复杂度分析,在我看来,这是数据结构与算法中最重要的知识点,且不接受任何反驳。

复杂度分析主要就是时间复杂度和空间复杂度,接下来的文章也主要围绕这两方面来讲。废话不多说,前排马扎瓜子准备好,蛋蛋小课堂正式接客
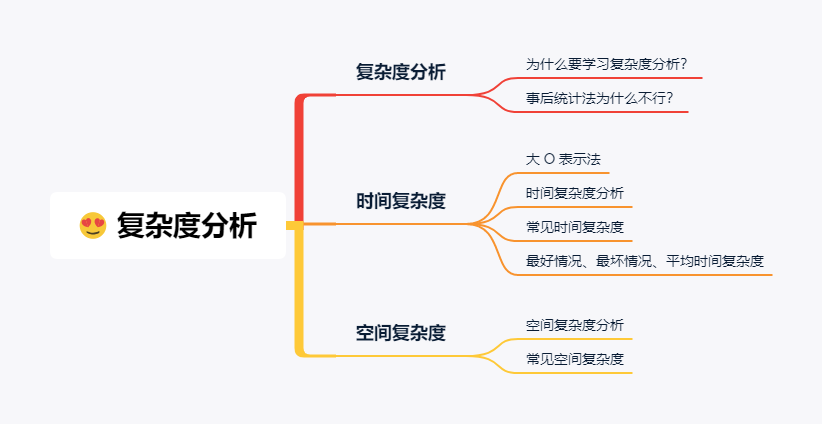
复杂度分析
刚刚我说过,在本蛋看来,复杂度分析是数据结构和算法中最重要的知识点,毫不夸张的说,这就是数据结构与算法学习的核心所在。你学会了它你就入的了门,你学不会它,你就永远不知道门儿在哪。
为什么复杂度分析会这么重要?
这个就要从盘古开天辟地,呃,从数据结构与算法的本身说起。
我平常白天做梦的时候,总是想着当当咸鱼划划水就能赚大钱,最好就是能躺着,钱就直接砸到我脑阔上。数据结构与算法虽然没有本蛋这么大的梦想,但是它的出现也是想着花更少的时间和更少的存储来解决问题。
那如何去考量“更少的时间和更少的存储”,复杂度分析为此而生。

既然你诚心诚意的不知道,那我就大发慈悲的打个不恰当的比方。
如果把数据结构与算法看成武功招式,那复杂度分析就是对应的心法。
如果只是学会了数据结构与算法的用法,不学复杂度分析,这就和你费尽千辛万苦在隔壁老王家次卧进门右手第二块地砖下偷挖出老王打遍村里无敌手的村林至宝王霸拳,然后发现秘籍上只有招式,没有内功心法,好好得王霸拳变的还不如王八拳。只有学会了王霸之气,才能虎躯一震,王霸之气一噗,震走村口光棍李养的哈巴狗。

吐样吐森破!吃葡萄不吐葡萄皮!
你们说的这种主流叫做事后统计法。
简单来说,就是你需要提前写好算法代码和编好测试数据,然后在计算机上跑,通过最后得出的运行时间判断算法时效的高低,这里的运行时间就是我们日常的时间。
我且不用“万一你费劲心思写好的算法代码本身是个很糟糕的解法”这种理由去反驳你,事后统计法本身存在很多缺陷,它并不是一个对我们来说有用的度量指标:
首先,事后统计法太依赖计算机的软件和硬件等性能。代码在 core i7 处理器的就比 core i5 处理器的运算速度快,更不用说不同的操作系统、不同的编程语言等软件方面,就算是在同一台电脑上,用的所有的东西都一样,内存的占用或者是 CPU 的使用率也会造成运行时间的差异。
再者,事后统计法太依赖于测试数据集的规模。同样是排序算法,你随便整 5 个 10 个的数排序,就算最垃圾的排序算法,也看起来快的和法拉利一样,如果是来10w 个 100w 个,那不同的算法的差距就很大了,而且同样是 10w 个 100w 个数,顺序和乱序的时间又不同了。
那么问题来了,到底测试数据集选多少个合适?数据的顺序如何定又算合适?
说不出来了叭?

可以看出,我们需要一个不依赖于性能和规模等外力影响就可以估算算法效率、判断算法优劣的度量指标,而复杂度分析天生就是干这个的,这也是为什么我们要学习并必须学会复杂度分析!
时间复杂度
时间复杂度,也就是指算法的运行时间。
对于某一问题的不同解决算法,运行时间越短算法效率越高,相反,运行时间越长,算法效率越低。
那么如何估算时间复杂度呢?
大佬们在拽掉脑阔上最后一根头发的时候发现,当用运行时间去描述一个算法快慢的时候,算法中执行的总步数显得尤为重要。
因为只是估算,我们可以假设每一行代码的运行时间都为一个 Btime,那么算法的总的运行时间 = 运行的总代码行数。
下面我们来看这么一段简单的代码。
def dogeggs_sum (n):sum = 0for dogegg in range(n):sum += dogeggreturn sum
在上面假设的情况下,这段求累加和的代码总的运行时间是多少呢?
第 2 行代码需要 1 Btime 的运行时间,第 4 和 第 5行分别运行了 n 次,所以每个需要 n * Btime 的运行时间,所以总的运行时间就是 (1 + 2n) * Btime。
我们一般用 T 函数来表示赋值语句的总运行时间,所以上面总的运行时间就可以表达成 T(n) = (1 + 2n) * Btime,翻译一下就是“数据集大小为 n,总步数为 (1 + 2n) 的算法的执行时间为 T(n)”。
通过公式,我们可以看出 T(n) 和总步数是成正比关系,这个规律的发现其实是很重要的,因为这个告诉了我们一种趋势,数据集规模和运行时间之间有趋势!
所有人准备,我们很熟悉的大 O 闪亮登场了!

大 O 表示法
大 O 表示法,表示的是算法有多快。
这个多快,不是说算法代码真正的运行时间,而是代表着一种趋势,一种随着数据集的规模增大,算法代码运行时间变化的一种趋势。一般记作 O(f(n))。
那么之前的公式就变成 T(n) = O(f(n)),其中 f(n) 是算法代码执行的总步数,也叫操作数。
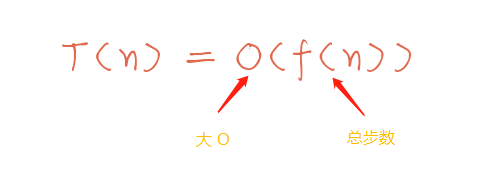
n 作为数据集大小,它可以取 1,10,100,1000 或者更大更大更大的数,到这你就会发现一件很有意思的事儿,那就是当数据集越来越大时,你会发现代码中的某些部分“失效”了。
还是以之前的代码为例。当 n = 1000 时,1 + 2n = 2001,当 n = 10000 时,1 + 2n = 20001,当这个 n 持续增大时,常数 1 和系数 2 对于最后的结果越来越没存在感,即对趋势的变化影响不大。
所以对于我们这段代码样例,最终的 T(n) = O(n)。
接下来再用两段代码进一步学一下求时间复杂度分析。
时间复杂度分析
代码 1
def dogeggs_sum (n):sum = 0for dogegg in range(n):for i in range(n):sum += dogegg * ireturn sum
这段代码我会从最开始一点点带你来。
第 2 行需要运行 1 次 ,第 4 行需要运行 n 次,第 5 行和第 6 行分别需要运行 n² 次。所以总的运行次数 f(n) = 1 + n + 2n²。
当 n 为 5 的时候,f(n) = 1 + 5 + 2 * 25,当 n 为 10000 的时候,f(n) = 1 + 10000 + 2 * 100000000,当 n 更大呢?
这个时候其实很明显的就可以看出来 n² 起到了决定性的作用,像常数 1,一阶 n 和 系数 2 对最终的结果(即趋势)影响不大,所以我们可以把它们直接忽略掉,所以执行的总步数就可以看成是“主导”结果的那个,也就是 f(n) = n²。
自然代码的运行时间 T(n) = O(f(n)) = O(n²)。
代码 2
def dogeggs_sum (n):sum1 = 0for dogegg1 in range(n):sum1 += dogegg1sum2 = 0for dogegg2 in range(n):for i in range(n):sum2 += dogegg2 * isum3 = 0for dogegg3 in range(n):for i in range(n):for j in range(n):sum3 += dogegg3 * i * jreturn sum1 + sum2 + sum3
上面这段代码是求三部分的和,经过之前的学习应该很容易知道,第一部分的时间复杂度是 O(n),第二部分的时间复杂度是 O(n²),第三部分是 O(n³)。
正常来讲,这段代码的 T(n) = O(n) + O(n²) + O(n³),按照我们取“主导”部分,显然前面两个小弟都应该直接 pass,最终 T(n) = O(n³)。
通过这几个例子,聪明的小婊贝们肯定会发现,对于时间复杂度分析来说,只要找起“主导”作用的部分代码即可,这个主导就是最高的那个复杂度,也就是执行次数最多的那部分 n 的量级。
剩下的就是多加练习,有意识的多去想多去练,就可以和我一样 帅气 稳啦。

常见时间复杂度
算法学习过程中,我们会遇到各种各样的时间复杂度,但纵使你代码七十二变,几乎也逃不过下面这几种常见的时间复杂度。
| 时间复杂度 | 阶 | f(n) 举例 |
| 常数复杂度 | O(1) | 1 |
| 对数复杂度 | O(logn) | logn + 1 |
| 线性复杂度 | O(n) | n + 1 |
| 线性对数复杂度 | O(nlogn) | nlogn + 1 |
| k 次复杂度 | O(n²)、O(n³)、.... | n² + n +1 |
| 指数复杂度 | O(2n) | 2n + 1 |
| 阶乘复杂度 | O(n!) | n! + 1 |
上表的时间复杂度由上往下依次增加,O(n) 和 O(n²) 前面已经讲过了,O(2n) 和 O(n!) 效率低到离谱,以后不幸碰到我再提一下,就不再赘述。
下面主要来看剩下几种最常见的时间复杂度。
O(1)
O(1) 是常数时间复杂度。
在这你要先明白一个概念,不是只执行 1 次的代码的时间复杂度记为 O(1),只要你是常数,像 O(2)、O(3) ... O(100000) 在复杂度的表示上都是 O(1)。
n = 10000res = n / 2print(res)
比如像上面这段代码,它运行了 3 次,但是它的时间复杂度记为 O(1),而不是 O(3)。
因为无论 n 等于多少,对于它们每行代码来说还是只是执行了一次,代码的执行时间不随 n 的变化而变化。
O(logn)
O(logn) 是对数时间复杂度。首先我们来看一段代码:
dogegg = 1while dogegg < n:dogegg = dogegg * 2
根据之前讲的,我们先找“主导”,在这主导就是第 4 行代码,只要算出它的时间复杂度,总的时间复杂度就知道了。
其实很简单,上面的代码翻译一下就是初始化 dogegg = 1, 乘上多少个 2 以后会 ≥ n。

假设需要 x 个,那么相当于求:
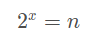
即:
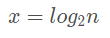
所以上述代码的时间复杂度应该为 O(log2n)。
但是对于对数复杂度来说,不管你是以 2、3 为底,还是以 10 为底,通通记作 O(logn),这是为什么呢?
这就要从对数的换底公式说起。
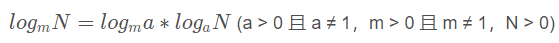
根据换底公式,log2n 可以写成:
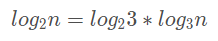
对于时间复杂度来说:
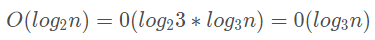
所以在对数时间复杂度中我们就忽略了底,直接用 O(logn) 来表示对数时间复杂度。
O(nlogn)
O(nlogn),真的是很常见的时间复杂度,像后面会学到的快速排序、归并排序的时间复杂度都是 O(nlogn)。
如果只是简单看的话是在 logn 外面套了层 for 循环,比如像下面这段代码:
def stupid_cnt(n):cnt = 0for i in range(n):dogegg = 1while dogegg < n:dogegg = dogegg * 2cnt += 1return cnt
当然像上面这种 stupid 代码一般人不会写,我也只是举个例子给大家看,我是狗蛋,大家千万不要以为我是傻狗。

最好情况、最坏情况和平均情况时间复杂度
除了数据集规模影响算法的运行时间外,“数据的具体情况”也会影响到运行时间。
我们来看这么一段代码:
def find_word(lst, word):flag = -1for i in range(len(lst)):if lst[i] == word:flag = ibreakreturn flag
上面这段简单代码是求变量 word 在列表 lst 中出现的位置,我用这段来解释“数据的具体情况”是什么意思。
变量 word 可能出现在列表 lst 的任意位置,假设 a = ['a', 'b', 'c', 'd']:
当 word = 'a' 时,正好是列表 lst 的第 1 个,后面的不需要再遍历,那么本情况下的时间复杂度是 O(1)。
当 word = 'd' 或者 word = 'e' 时,这两种情况是整个列表全部遍历完,那么这些情况下的时间复杂度是 O(n)。
这就是数据的具体情况不同,代码的时间复杂度不同。
根据不同情况,我们有了最好情况时间复杂度、最坏情况时间复杂度和平均情况时间复杂度这 3 个概念。
最好情况时间复杂度
最好情况就是在最理想的情况下,代码的时间复杂度。对应上例变量 word 正好是列表 lst 的第 1 个,这个时候对应的时间复杂度 O(1) 就是这段代码的最好情况时间复杂度。
最坏情况时间复杂度
最坏情况就是在最差的情况下,代码的时间复杂度。对应上例变量 word 正好是列表 lst 的最后一个,或者 word 不存在于列表 lst,这个时候对应的时间复杂度 O(n) 是这段代码的最坏情况时间复杂度。
平均情况时间复杂度
大多数情况下,代码的执行情况都是介于最好情况和最坏情况之间,所以又出现了平均情况时间复杂度。
那怎么计算平均时间复杂度呢?这个说起来有点复杂,需要用到概率论的知识。
在这里我还是用上面的例子来讲,因为只是简单的科普一下,为了方便计算,我假设的会有点随意:
从大的方面来看,查找变量 x 在列表 lst 中的位置有两种情况:在或者不在。假设变量 x 在或者不在列表 lst 中的概率都为 1/2。
如果 x 在列表 lst 中,那么 x 有 n 种情况,它可能出现在 0 到 n-1 中任意位置,假设出现在每个位置的概率都相同,都为 1/n。
每个出现的概率(即权重)知道了,所以平均时间复杂度为:
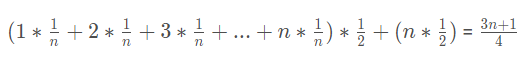
是不是看着有点眼熟,这就是我们都学过的加权平均值。
什么,没学过?问题不大。加权平均值就是将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。
所以最终的平均时间复杂度就为:
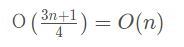
最好情况,反应最理想的情况,怎么可能天上天天掉馅饼,没啥参考价值。
平均情况,这倒是能反映算法的全面情况,但是一般“全面”,就和什么都没说一样,也没啥参考价值。
最坏情况,干啥事情都要考虑最坏的结果,因为最坏的结果提供了一种保障,触底的保障,保障代码的运行时间这个就是最差的,不会有比它还差的。
所以,不需要纠结各种情况,算时间复杂度就算最坏的那个时间复杂度即可。
空间复杂度
空间复杂度相较于时间复杂度来说,比较简单,需要掌握的内容不多。
空间复杂度和时间复杂度一样,反映的也是一种趋势,只不过这种趋势是代码运行过程中临时变量占用的内存空间。
代码在计算机中的运行所占用的存储空间呐,主要分为 3 部分:
代码本身所占用的
输入数据所占用的
临时变量所占用的
前面两个部分是本身就要占这些空间,与代码的性能无关,所以我们在衡量代码的空间复杂度的时候,只关心运行过程中临时占用的内存空间。
空间复杂度记作 S(n),表示形式与时间复杂度一致。
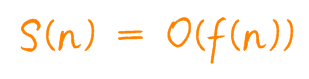
在这同样 n 作为数据集大小,f(n) 指的是规模 n 所占存储空间的函数。
空间复杂度分析
下面我们用一段简单代码来学习下如何分析空间复杂度。
def dogeggs_sum(lst):sum = 0for i in range(len(lst)):sum += lst[i]return sum
上述代码是求列表 lst 的所有元素之和,根据之前说的,只计算临时变量所占用的内存空间。
形参 lst 所占的空间不计,那么剩下的临时变量只有 sum 和 i,sum 是存储和,是常数阶,i 是存储元素位置,也是常数阶,它俩所分配的空间和规模 n 都没有关系,所以整段代码的空间复杂度 S(n) = O(1)。
常见空间复杂度
常见的空间复杂度有 O(1)、O(n)、O(n²),O(1) 在上节讲了,还有就是像 O(logn) 这种也有,但是等闲不会碰到,在这里就不罗嗦了。
O(n)
def create_lst(n):lst = []for i in range(n):lst.append(i)return lst
上面这段傻傻的代码有两个临时变量 lst 和 i。
其中 lst 是被创建的一个空列表,这个列表占用的内存随着 for 循环的增加而增加,最大到 n,所以 lst 的空间复杂度为 O(n),i 是存储元素位置的常数阶,与规模 n 无关,所以这段代码最终的空间复杂度为 O(n)。
O(n²)
def create_lst(n):lst1 = []for i in range(n):lst2 = []for j in range(n):lst2.append(j)lst1.append(lst2)return lst1
还是一样的分析方式,很明显上面这段傻二次方的代码创建了一个二维数组 lst,一维 lst1 占用 n,二维 lst2 占用 n²,所以最终这段代码的空间复杂度为 O(n²)。
到这里,复杂度分析就全部讲完啦,只要臭宝们认真看完这篇文章,相信会对复杂度分析有个基本的认识。复杂度分析本身不难,只要多加练习,平时写代码的时候有意识的多想估算一下自己的代码,感觉就会慢慢来啦。
这是公众号的第一篇,写完真心不太容易,希望开了个好头。码字不易,臭宝们多多支持呀,点赞在看留言么么哒呀。
我是蛋蛋,我们下次见~

