Java实现-归并排序算法-动图详解
归并排序详解(后序遍历)
大家可能都对二叉树的后序遍历比较熟悉,实际上归并排序本质框架就是二叉树的后序遍历,根结点的遍历只不过换成了治(Merge方法的调用),本文将结合动图+代码的方式进行最通俗的讲解。
「基本思想」:利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案修补在一起,即分而治之)。
分的过程
下面自制配了一张动图来更好理解分的过程,其实完全就是左右根的后序遍历,根的遍历就是治(Merge方法的调用),分的过程中暂不可考虑根结点的遍历,动图中仅展示左边的分的过程,以mid将其分组,递归的终止条件就是left==right,每组的right和left都不相同,左边递归调用传值left的值不变,right值为mid,右边递归调用传值left为mid+1,因为mid是左边的最后一个,所以要加1,右边的值就是right。
代码如下:
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left != right) {//left和right的值会根据mid的值不断变化
int mid = (left + right) / 2;
//向左递归进行分解,动图分组中靠左的部分
mergeSort(arr, left, mid, temp);
//向右递归进行分解 动图分组中靠右的部分
mergeSort(arr, mid + 1, right, temp);
//合并(相当于根)下面动图中暂未表示合的思路
merge(arr, left, mid, right, temp);
}
}

如下图:「加上右边逻辑上大致呈现二叉树状」
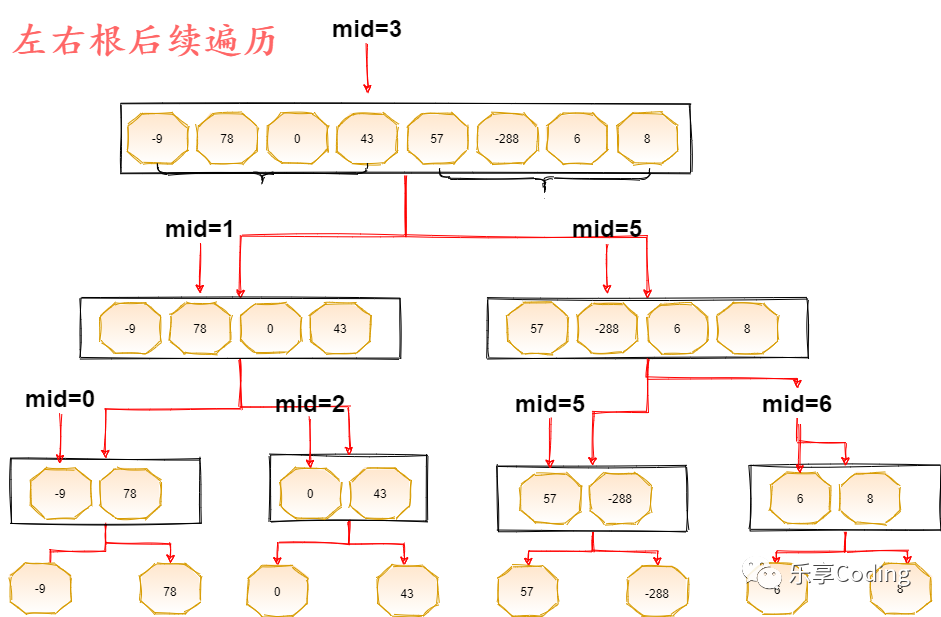
治---合的过程
根据二叉树后序遍历的特点,以本题为例,很明显根节点需要遍历7次,顺序如下图所示:

合并的规则如下:
定义一个与原数组长度相等的临时空数组temp,初始索引t=0,之后每次合并(共7次)左结点的起始索引为left,末尾索引为mid,右节点的起始索引为mid+1,末尾索引为right,利用while循环将左结点的每一个值与右结点的每一个值做比较,判断条件为(left <= mid && mid+1 <= right),如果左结点的值小于右结点的值,则将左结点的值赋给temp[t],之后t++,为保证不修改left的值所以将值赋给变量i,i++;相反如果右节点的值小于左结点的值,右结点的值赋给temp[t],之后t++,为保证不修改mid+1的值所以将值赋给变量j,j++;这步做完后,发现左右个结点一定会有值剩下,因为左右结点的值总会有一个先到达判断条件,++之后就终止了while循环,因此会剩余,这时又会出现两种情况,一是左边剩余(可能不止一个),另一个是右边剩余(可能不止一个),因此还需要while循环,如果左边剩余说明还没到达mid(结尾索引),判断条件为(i <= mid),剩余元素一定是有序的并且是较大值,因此只需添加到临时数组temp的末尾即可,右结点有值剩余只不过判断条件变为(j <= right),方法一样。
最后每次合并都将temp的值copy到传入的数组中去即可!
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;//左边有序序列的初始索引
int j = mid + 1;//右边有序序列的初始索引
int t = 0; //指向temp数组的当前索引
//一
//先把左右两边有序的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) { //继续
//如果左边的有序序列的当前元素小于等于右边有序序列的当前元素
//即将左边的当前元素填充到temp数组
//然后t++,i++
if (arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else { //反之,则将右边的有序序列当前元素填充到temp数组
temp[t] = arr[j];
t += 1;
j += 1;
}
}
while (i <= mid) {//将左边剩余元素全部填充进temp中
temp[t] = arr[i];
t += 1;
i += 1;
}
while (j <= right) {//将右序列剩余元素全部填充进temp中
temp[t] = arr[j];
t += 1;
j += 1;
}
//三
//将temp数组的元素拷贝到arr
//注意,并不是每次都拷贝所有
t = 0;
int tempLeft = left;
//第一次合并tempLeft=0,right=1 tempLeft=2,right=3 tempLeft=0,right=3
//最后一次tempLeft=0,right=1
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
「由于合并次数过多,下图仅将最后一次合并图解在下图」:
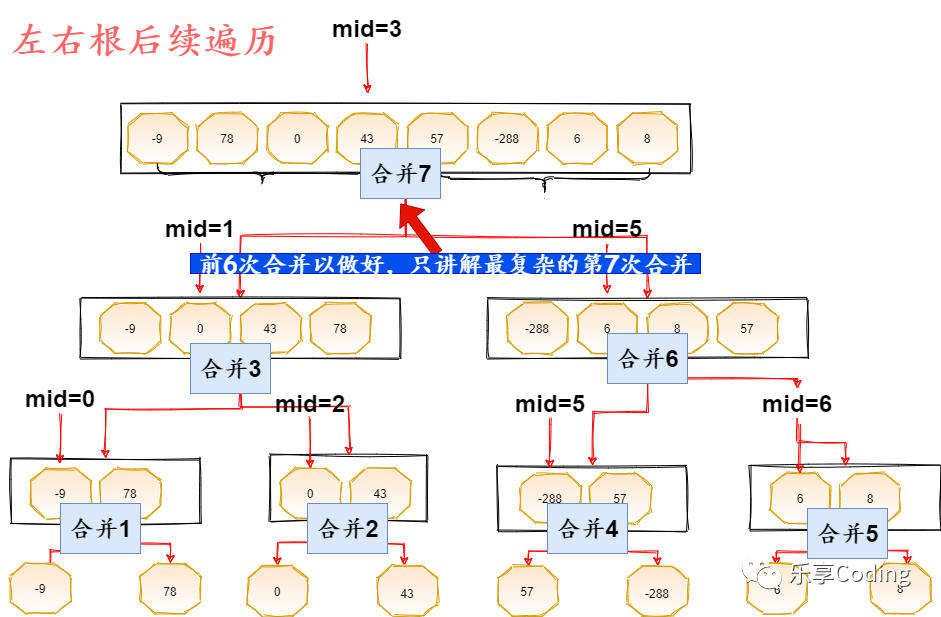
「第七次合并动图图解:」
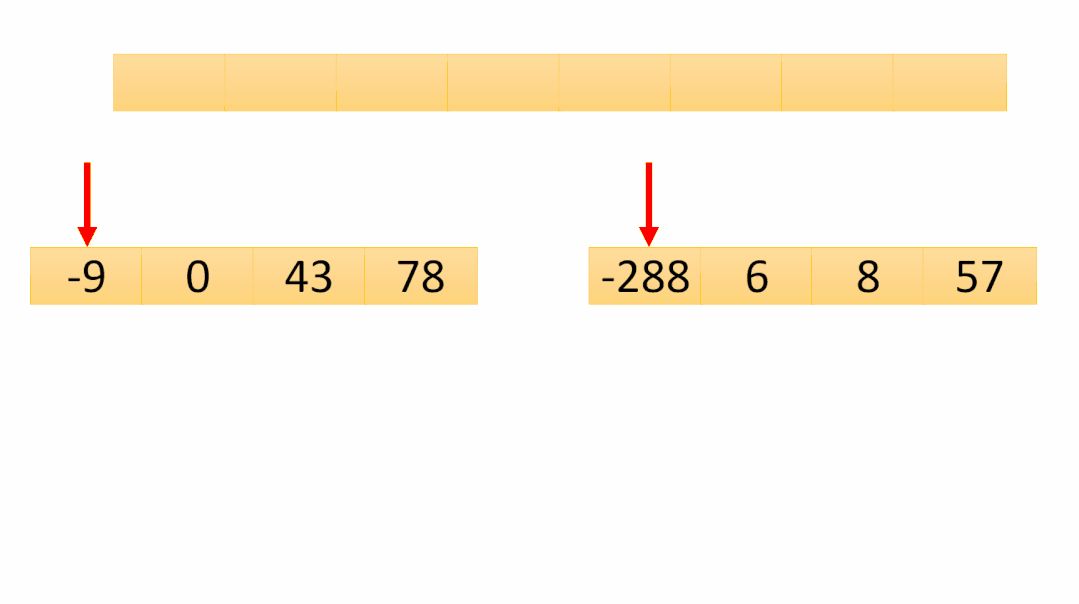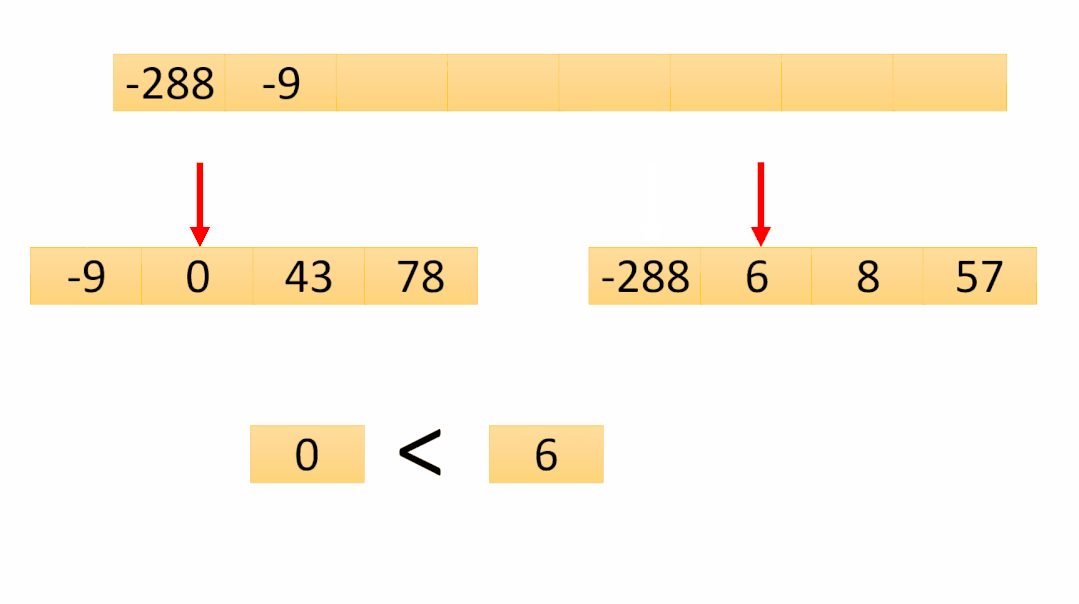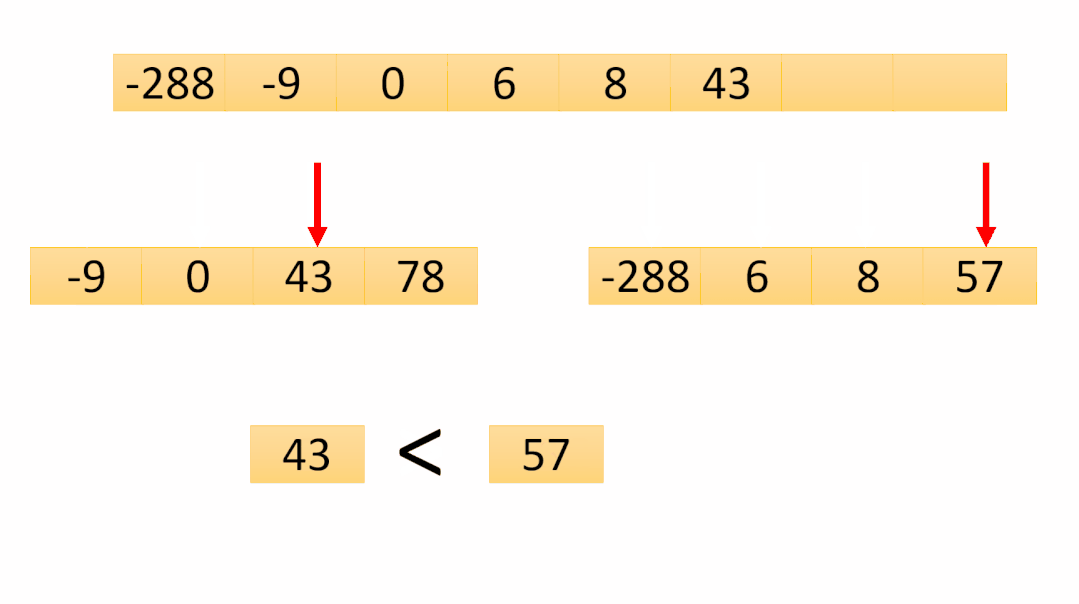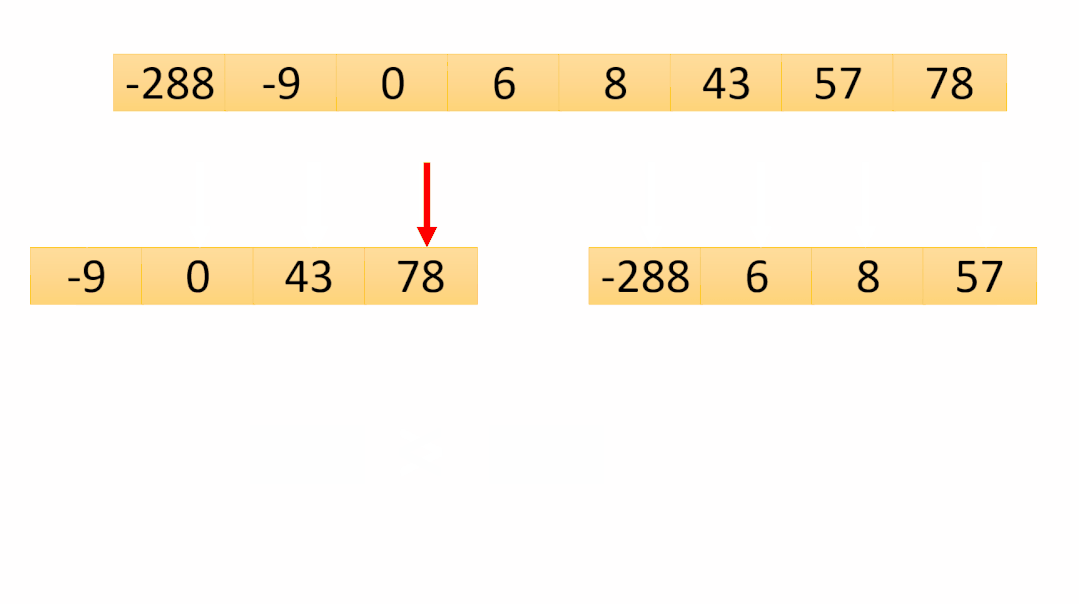
第七次合并是最后一次合并,可以看到数组已经有序了,最后将temp数组copy到原数组即可排序完成!
时间复杂度:O(nlogn)
空间复杂度:O(n+logn)
由于归并排序在归并过程中需要与原始记录序列同样数量的存储空间存放归并结果以及递归深度为log2n的栈空间,因此空间复杂度为O(n+logn),会造成空间的浪费,因此可采用迭代继续优化,但是思路比较复杂,在本篇文章不做讲解!
