你会玩数独么?
周六去公园晃了一圈,来了顿有仪式感的野餐下午茶。周日宅在家里,实在无聊的很,睡个懒觉,半天就打发过去了。看看冲天在哪里啊的电视剧,转眼到了晚上。鉴于仙女实在无聊的很,于是我主动挑事,要和仙女一起做数独。
“哎呀,做数独一点都不锻炼脑子的,实在是无聊的很”,仙女名言。作为一个纯粹的工科生,我是一点都不信的,数独还是很考验综合能力的,眼睛要扫描的快,排除要迅速,验证可能性要准确。遇到不确定的地方还要做假设。
前几场的战绩,很惨淡,每次都是以我惜败告终。(其实不是惜败,是大败,被仙女甩几条街了)。今天我又不服,想靠运气战胜仙女。话不多说,上题。
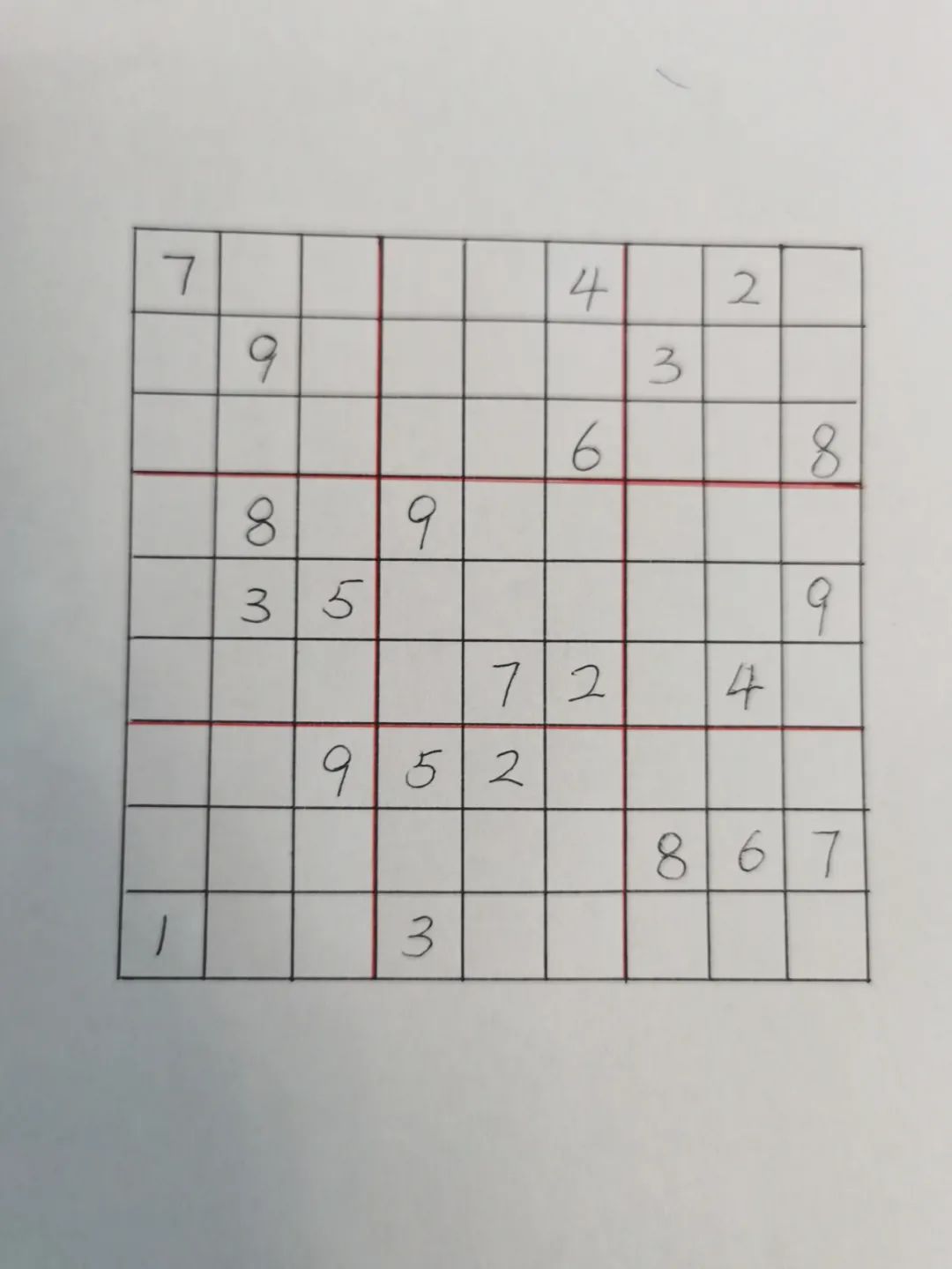
距离困觉时间还早,我不服气向仙女发出第二次挑战。这次是在电脑上做题目,我一下子就来劲了,脑子放光。因为电脑上excel,多建几个sheet,每个框多填几个可选数字还是非常方便的。于是网上找了个题目,新一轮battle开始。
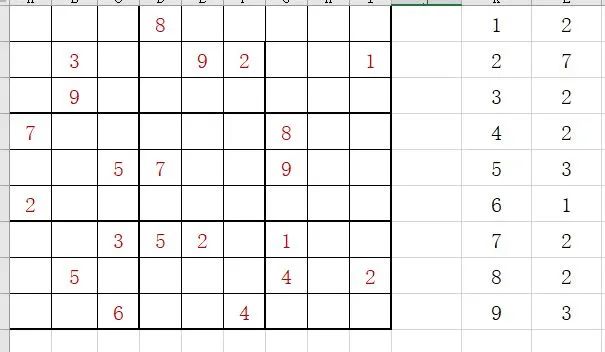
时间一下子穿越到40分钟之后,除了极少数确定的,我一点进展都没有,已经新建了好几个excel里面的sheet,还没遇到一个碰壁回头尝试失败的,也没有哪种情况顺利做到最后。而此时,仙女在她众多的猜测里,终于找到了一个答案。顿时感觉智商被碾压。接下来放一下我和仙女的思路对比。
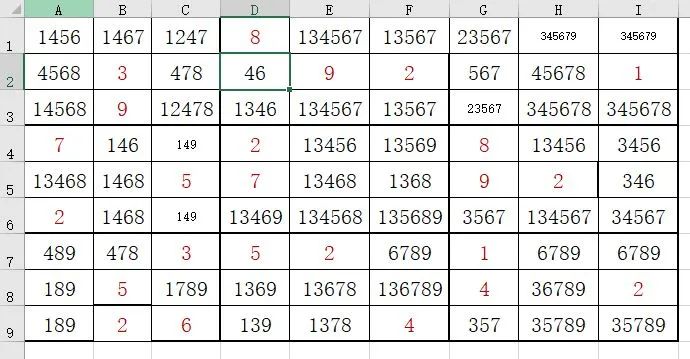
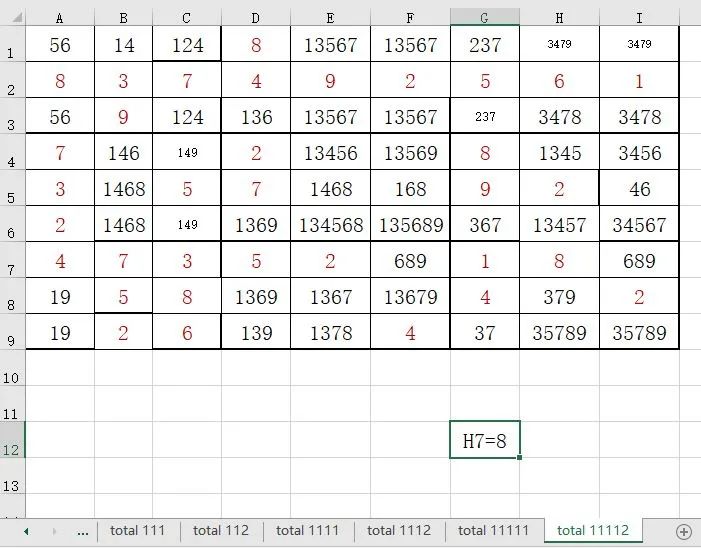
一顿分叉,从total总的数据,到total11111,total11112,还在继续分叉。仙女的思路差不多,不过她的执行效率更高,对excel的熟练度也相当高。仙女解题过程如下:先列出总的数据,这步骤和我一样。
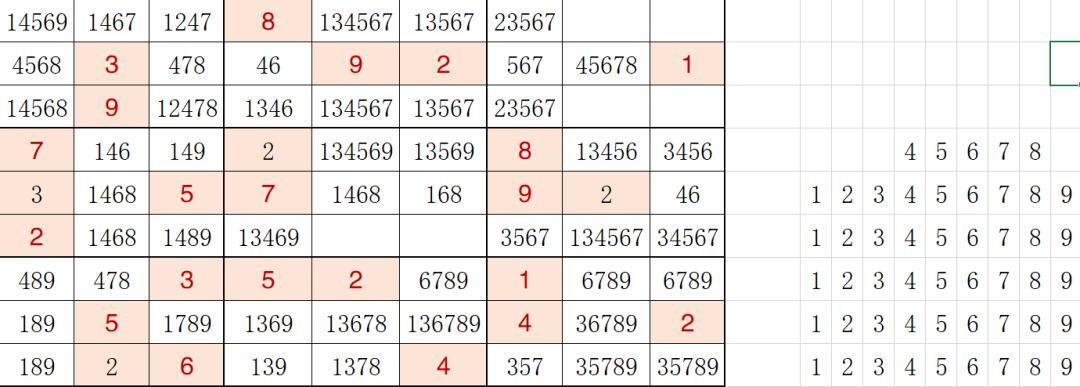
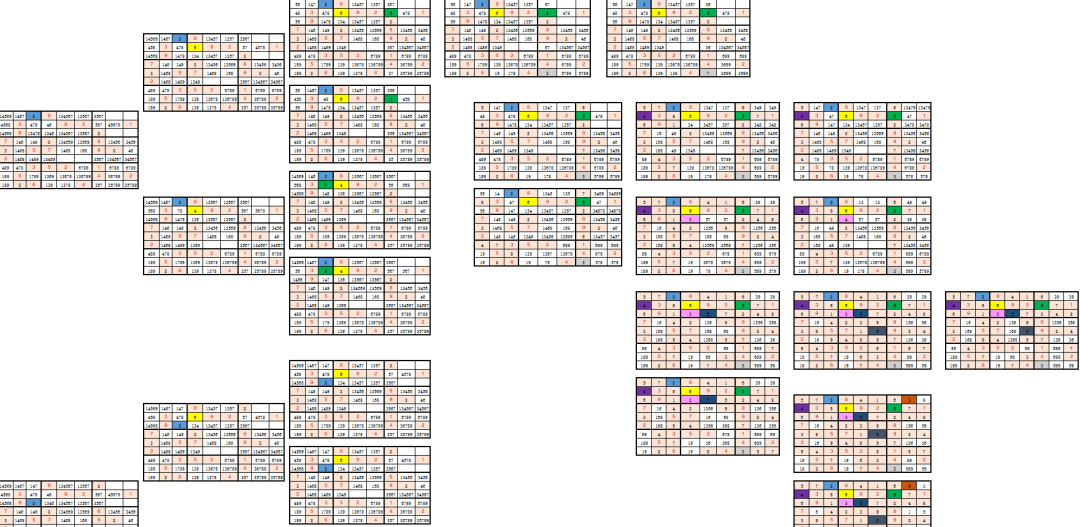
第一个要考虑的问题是,怎样表示数独。这里使用一个嵌套的list。空的地方填0,其他地方把题目中的数据填进来。
board = [[0,0,0,8,0,0,0,0,0],[0,3,0,0,9,2,0,0,1],[0,9,0,0,0,0,0,0,0],[7,0,0,0,0,0,8,0,0],[0,0,5,7,0,0,9,0,0],[2,0,0,0,0,0,0,0,0],[0,0,3,5,2,0,1,0,0],[0,5,0,0,0,0,4,0,2],[0,0,6,0,0,4,0,0,0],]
参考了网上一些写好的数独程序,发现基本没有做原始数据检查的,看来很信得过出题的人。鉴于题目录入的时候,有输错的可能性,所以在正式解数独之前,先检查一下板子的数据是否正常。板子的检查,包括每一行,每一列,还有每个九宫格。这里的检查方法,使用Counter把每一行列九宫格中的数据检查一下数量。空着的数据用0表示,所以0会有多个,其他数据应该只有1个或者是没有。
def check_repeat(self,data): #检查输入的9个数是否有重复c = dict(Counter(data))# print(c)for key, v in c.items():if key == 0:passelse:if v != 1:# print('有重复数据')return Falsereturn Truedef check_row(self): #检查所有行是否有重复数据for row in range(0,9):result = self.check_repeat(self.b[row])if result == False:return resultreturn Truedef check_column(self): #检查所有列是否有重复数据list = np.array(self.b)for column in range(0, 9):result = self.check_repeat(list.T[column])if result == False:return resultreturn Truedef check_square(self): #检查所有九宫格是否有重复数据square = []for i in range(0,9):row, col = int(i / 3) * 3, int(i % 3) * 3square.append(self.b[row][col:col+3]+self.b[row+1][col:col+3]+self.b[row+2][col:col+3])# print(square[i])result = self.check_repeat(square[i])if result == False:return resultreturn Truedef check_board(self): #检查输入的数独是否有输入错误result = self.check_row() and self.check_column() and self.check_square()return result
在这顿没啥用的操作之后,可以正式开始解题了。我相信大多数小伙伴都会想到穷举法,没错这是个万能的方法,我就一个一个去试呗。但是这样做很蠢,效率也不高。
可以使用递归算法加上剪枝。(在算法面前,我个弱鸡不值一提) 递归的思想很重要,如果不理解递归的思想,是很难把代码写好的。在这里我们以青蛙跳为例子:一只青蛙一次可以跳1个台阶或者2个台阶,现有一个10级高的台阶,青蛙跳上去一共有多少种方案?这是个很典型的递归,思考方法可以逆推。最后青蛙是跳完了这10个台阶,那么最后一步要么是跳了1步,要么是跳了2步。所以总的方法就等于最后一步跳1与跳2的方案之和,这样一直一直往前推,就能推到初始没有跳的状态。
递归的核心,有明确的初始状态值,每一步计算的表达式清晰,每一步计算前后有关联性。以斐波拉契为例,f(1)=1,f(2)=1,f(3)=2... 可以看到f(3) = f(2)+f(1)。本题求解数独问题,最后一个步骤肯定是填写最后一个空格上的数据,如果填对了,那么数独计算结束。如果找不到合适的值,那么就往上回归,上一个步骤是错的,得换个值来计算。理论不多说,直接上代码。
根据人做数独的思路,先找到每个格子上可以填的数字的个数和具体内容是什么。然后挑选可填数字数量最小的开始尝试。见cal_count和cal_count_all(如果数字是1,说明只有1种选择,那么这个数字填写起来就很快。如果有2种数字可以填,那么就需要填好一个继续往下面试试。出题自带的原始数据,使用10来表示)try_it函数需要结合刚才说的递归的思想好好理解一下。最后运行程序,biu~ 780ms,出来了15种数独解决方案,可见这一题是多解。如果只要做出一种方案,运行时间为80ms。运行速度,还算凑合,使用c,c++来解题,速度可以再高一档次。众所周知,c的运行效率是python的10倍。(我瞎说的),但是编程时间却是python的10倍不止。def cal_count(self,x,y):count = 9value = [1,2,3,4,5,6,7,8,9]row = self.b[x] #一行数据column = list(np.array(self.b).T[y]) #一列数据x, y = int(x / 3) * 3, int(y / 3) * 3square = self.b[x][y:y + 3] + self.b[x + 1][y:y + 3] + self.b[x + 2][y:y + 3]data = list(set(row+column+square))data.remove(0)count = count-len(data)for i in range(len(data)):value.remove(data[i])return count,valuedef cal_count_all(self):count = []value = []# index = 0for i in range(0, 9):for j in range(0, 9): #遍历整个数独,每个位置检查横向纵向九宫格# index = index+1if self.b[i][j] != 0:value.append(self.b[i][j])count.append(10) #题目中填好的数字else:tmp_count,temp_value = self.cal_count(i,j)# 增加一个打断,如果检测到一个格子里只有1种或者2种解法,后面的就不用计算了# if (tmp_count == 1):# print(tmp_count, index, temp_value)# return tmp_count, index, temp_valuecount.append(tmp_count)value.append(temp_value)#遍历完之后,每个格子都有3种或者以上的填法# print(count)min = np.min(count)index = int(np.argmin(count))# print(min,index)return min,index,value[index]def try_it(self,min,index,value):#主循环self.t += 1if min == 10:print('数独破解完成,一种可能的结果如下:')for i in self.b:print(i)# print(self.b)return True # 返回Trueelse:x, y = int(index / 9), int(index % 9)for i in value: #从筛选过后的值填入self.b[x][y]=i #将符合条件的填入0格next_min,next_index,next_value= self.cal_count_all() #找出下一个可填数字最少的格子end=self.try_it(next_min,next_index,next_value)if not end: #在递归过程中存在不符合条件的,即 使try_it函数返回False的项self.b[x][y] = 0 #回朔到上一层继续#不添加以下两句的话,数组得出一个方案之后不会结束,会继续测试value里面的其他值,可以用于求解多解法的数独,加上之后,只会打印一种方案else:return Truereturn False #屏幕上填满数字,最后一次try还是失败了,返回false
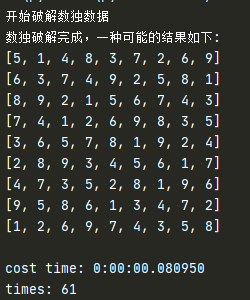
虽然没使用上高级的算法,好多判断方法不是最高效,有重复检查计算的部分,没有及时砍枝再继续计算。但总的来说,ms级就可以把问题解决,相比于两个憨憨写个40分钟还不一定写的出来答案来说,已经很不错了。完整代码点击阅读原文,进入git。好了,以后做数独,仙女再也不是我的对手,接下来该PK什么新技能呢?
相关文章:
