光学计算 - 高效获取光传输矩阵
点击上方“小白学视觉”，选择加"星标"或“置顶”
重磅干货，第一时间送达
转自|计算摄影学
一. 背景
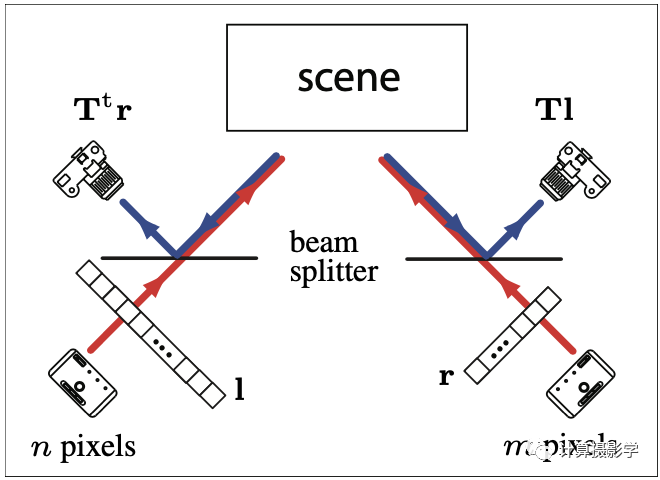
光传输矩阵（下图中的T），它包含了场景中从光源l到目标图像p的所有关键信息。
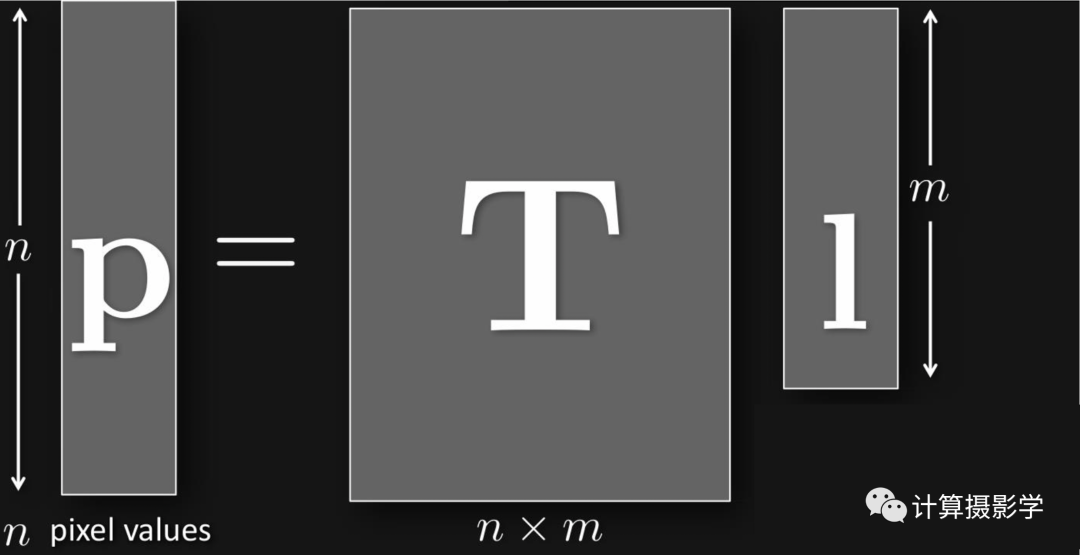
获取光传输矩阵，对Relighting、光度立体以及对偶摄影等等应用场景中都非常重要。
然而，高效的获取光传输矩阵非常困难，如下图所示。T的尺寸是 
，如果输入光源尺寸为100万点，相机传感器像素为100万像素，那么T的尺寸将高达 
而且，这还只是一个简化的例子。事实上T通常是非对称的，结构复杂，这给获取它带来了更多困难。因此有大量的研究集中在高效高质量的获取光传输矩阵，这些研究通常会采用很多复杂的数值计算方法。
我今天想简介的，是一个全新的获取光传输矩阵并加以应用的思路，看完后让人不禁眼界大开。这个技术来自于下面这篇论文：
这篇文章的一个核心思想是：虽然直接获取T是非常困难的，但光传输矩阵T、光源l以及最终成像的图像p之间确实有明确的关系
因此，可以利用这个特性，高效的实现一些会利用到Tl的数值计算算法。
二. 光学计算介绍
2.1 幂迭代算法获取方阵主特征向量
先从最简单的例子看起，这个例子介绍了一种叫做幂迭代法(Power Iteration)的算法，它的目标是获取一个方阵的主特征向量，过程非常简单易懂：
你可以看到这里应用到了 
，因此很容易将它变成一个用特定光源 
照射场景，并捕获图像 
的过程。
2.2 Krylov子空间法: 求解大型线性系统的一些最重要的迭代算法
由幂迭代算法获取的一系列向量形成了Krylov子空间：
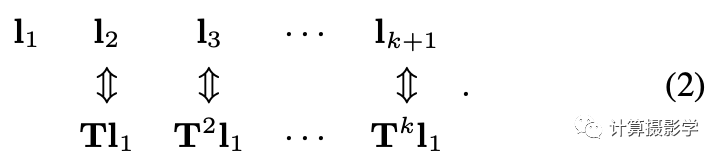
基于这个子空间有一系列用于分析大型线性系统的迭代算法。由于光传输矩阵T正好也是形态各异的大型矩阵，因此也很适合用光学计算来代替这些算法中的数值计算部分。
作者介绍了两种算法，一种叫做Arnoldi，它用于获取大型矩阵T的一个低秩的近似矩阵。另外一种则叫做GMRES（广义最小残差法），它可以用于反向光传输，例如用于我之前介绍过的对偶摄影中。
2.2.1 Arnoldi算法
当我们的诉求是对场景进行打光渲染时，可以用一个秩为K的小矩阵来近似替代全尺寸的光学传输矩阵。这个过程可以用Arnoldi算法来实现。
这个算法和幂迭代法的总体结构是一致的，我们来看看它们的区别：
这里面，ortho函数的作用是将pk投影到l1....lk的正交子空间中。
所以看起来Arnoldi的算法过程和幂迭代法是一致的。然而，由于Arnoldi算法的实现过程中，光照向量l中的值可以是负数，且T矩阵不一定是方阵，因此就多了一些变化，因此在用光学计算代替数值计算的过程中就有一些计算要点：
要点1：矩阵与任意向量的乘积
在Krylov的一系列算法中，通常会需要计算矩阵T与任意向量l的乘积，其中l的元素值可能有正，有负，而我们是无法用一个“负的光源”去作用于场景的。怎么解决这个问题呢？
很简单，可以用两个光源，一个代表正值元素( 
)，一个代表负值元素( 
)。然后通过两次成像，并将成像的结果相减，来得到Tl的值
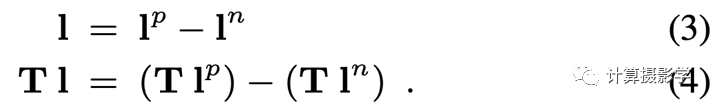
要点2：解决T矩阵可能不对称的问题
先看T矩阵什么情况下会是对称的。通常来说，这要求投影仪投出的图像和相机传感器的分辨率一致，而且两者的视角也是一致的，如下图所示。很显然，这种安排的作用很有限。
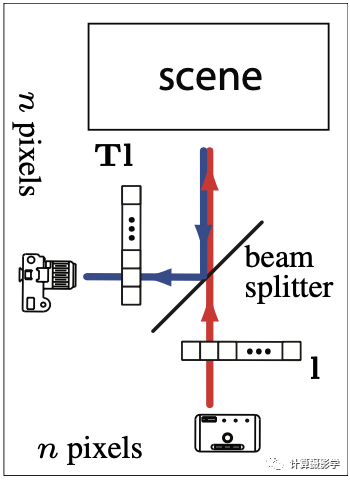
但我们可以先计算构造对称矩阵T*
然后就可以很方便的沿用幂迭代算法的思想来分析T*了，这里：
这个式子用单个相机和投影仪的组合是很难做到光学实现的，但用两对相机+投影仪的组合则可以办到。
这里面左投影仪投射的图案由右相机成像，而右投影仪发出的图案由左相机成像。
采用上述两个技术要点，就有了两种情况下的Arnoldi算法实现：
下面的视频展示了一个典型的过程
事实上，如果仅仅是想对场景进行重照明，可以不用计算出完整的近似矩阵，而只需要利用Arnoldi算法生成的一系列中间光照向量 和图像 
即可
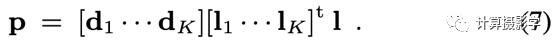
这里第一步是把新的用于照明场景的l投影到 
的空间中得到光照向量，然后用它的各个分量作为权重，将arnoldi算法过程中得到的子图像 加权起来即可得到重照明的图像。
下面这个视频展示了重照明的结果，注意帽子所投射的复杂阴影(既尖锐又柔软)，头发和阴影中的复杂亮点，以及玻璃场景中的阴影、焦散和间接照明效果都非常逼真。
上面的视频中仅仅用了40次迭代即可获得很好的结果。我们来看看当迭代次数变化时对结果的影响，注意这里我们打光时用了点光源：
2.2.1 GMRES算法
如果仅仅知道一幅照片，我们想知道它是在什么样的光照情况下产生的，这时候就需要用到GMRES（广义最小残差）算法。
注意此时我们既不知道光源向量，也不知道光传输矩阵。这时候的算法其实和幂迭代法、Arnoldi算法具有一致的形态，其区别如下。其中上标+代表矩阵的伪逆
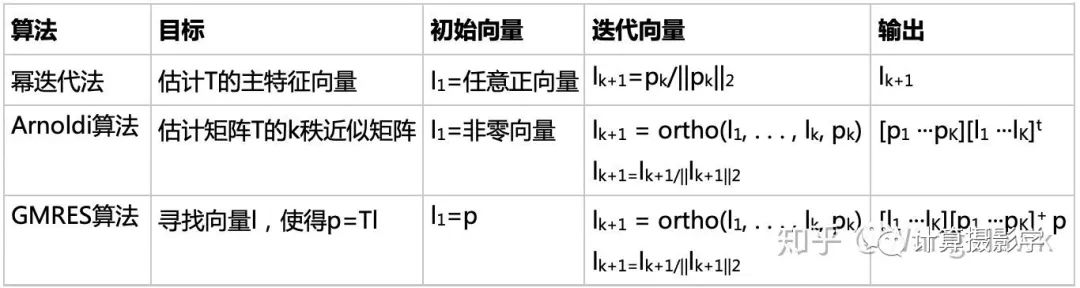
可以看到，它与Arnoldi算法唯一的区别就是输入的向量 
, 以及返回值。注意这里，为了求得光源l，同样也不需要真的求解出T，而只需用kyrlov空间中的一系列向量 
，以及 
即可。
三. 评价和总结
正如作者在论文中所述，本文最大的贡献是在光域上替代复杂的数值计算。文中描述的Arnoldi算法以及GMRES算法仅仅是作者为了展示这种思想的两个例子而已。事实上，作者说最关键是传统上认为必须要获取光传输矩阵T才能实现的一些操作，可以完全脱离T而实现。这就启发了后续更大量的研究。
实际上，就我看来，这恰好是利用模拟器件来取代某些数字计算来提高效率的一个明证。其他的例子还有很多.
总之，通过本文我们再次强化了计算摄影学不仅仅是成像、图像处理的认知，“计算”本身也可以是这个学科的研究内容和应用方向。
四. 参考资料
CMU 2017 Fall Computational Photography Course 15-463, Lecture 22
O’Toole and Kutulakos, “Optical computing for fast light transport analysis,” SIGGRAPH Asia 2010.