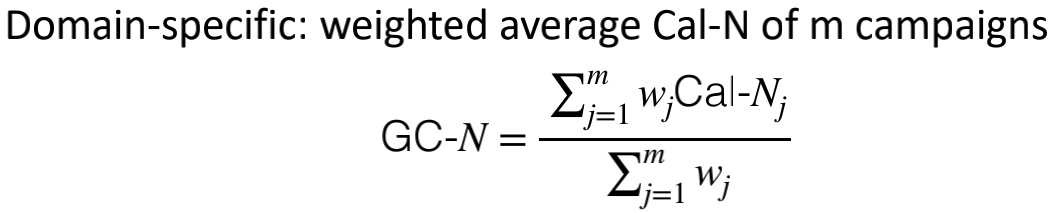本文将介绍校准算法在阿里妈妈展示广告中的应用和演进,将从背景介绍、校准算法演进、工程实践以及总结展望四个方面展开介绍。
[ 导读 ]校准技术是可信机器学习领域的一个研究分支,它能够改善机器学习模型在预估准确度和置信度方面的不确定性,在医疗诊断、气象预测、自动驾驶以及计算广告领域具有重要的应用。本文将介绍校准算法在阿里妈妈展示广告中的应用和演进,将从背景介绍、校准算法演进、工程实践以及总结展望四个方面展开介绍。01 背景介绍
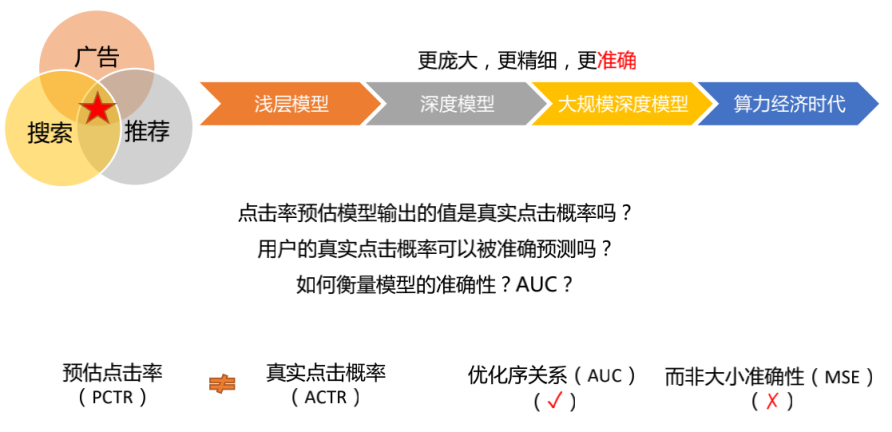
首先介绍校准的概念,并举例说明在计算广告中为什么需要对预估值进行校准。用户行为概率预估技术(点击率、转化率、短视频3s曝光率等)是搜索、推荐以及计算广告领域的核心技术能力。随着深度学习技术的发展,预估模型在过去几年中也经历了快速的迭代,不断向更庞大、更精细、更准确的方向演进。但是预估模型真的变得更准确了吗?不失一般性,我们以计算广告中的点击率预估模型为例,思考以下几个问题:
① 用户的真实点击概率是可以被准确观测的吗?
点击率是指“用户在某个时刻对曝光广告进行点击的概率”。理论上每条流量都存在一个潜在的点击概率,从统计意义上来讲,如果存在平行空间将广告曝光给某个用户的事件重复多次,则可以根据大数定律将用户的点击概率估算出来。但是在真实世界中,我们能且仅能观察到事件的单次发生(点击与否),所以是无法准确观测到任意样本的真实点击概率的。
② 点击率预估模型的准确性偏差原因是什么?
因为真实点击概率是不可以被准确观测到的,所以点击率预估模型也不能直接对点击率进行回归预测。现有点击率预估模型通常从统计视角对问题进行抽象和简化,假设特征和点击事件的联合分布服从某种函数形式(不同模型的假设分布不同),然后以Data-Driven的方式训练模型,实现对点击率的预测。但是该预测值是对真实点击概率的猜测,其预估偏差根本取决于分布假设与实际情况的差异程度,并受限于模型的真实学习效率。
③ 预估模型的准确性如何度量,AUC指标是足够的吗?
我们无法对预测结果从单样本粒度来度量其准确性(真实点击概率的不可预测性)。AUC是一种退而求其次从宏观层面对样本的比较关系进行度量的指标,反映了预测序关系对真实序关系的逼近程度。但是它无法表征预估值的“大小准确性”。大小准确性是指,如果广告点击率是1%,则意味着广告曝光10000次后将有100次被真实点击。如果低于100次,则意味着模型高估,反之则意味着模型低估。所以仅仅考虑序关系是不全面的,校准技术在本质上是一种在现有模型基础上进一步优化预估值大小准确性,使其尽可能逼近(近似)真实值的技术。
在计算广告中,模型预估值大小准确性的优化(预估校准)在出价准确性、稳定性(包括算法出价oCPX/Auto-Bidding等)、竟价公平性,计划冷启动等方面发挥重要作用。以下举两个简单的例子进行简要说明:如上图所示,广告竞价排名由平台期望收益eCPM决定,ad3的pCTR为1.0%,排序为3。如果ad3的pCTR被高估30%,则eCPM将从10变为13从而获得展示机会,从而导致ad3的拿量能力变大,但平台的期望收入降低。如上图所示,如果AD2的pCTR从1.1%被高估到1.2%,那么在GSP拍卖机制下,仍然是AD1赢得曝光机会,但是其扣费却从11变为12,导致AD1被多扣费,平台收入增加;反之,AD1如果从1.1%被低估为1.0%,则AD1会被少扣费,平台收入产生折损。以上两个例子说明在模型预估值大小发生偏差的情况下会明显导致广告主或平台的收益受损。除此之外,随着广告业务形态的发展,更多的场景对模型预估值大小准确性提出了挑战,包括:① 多种Bid类型混竞:CPC、CPM、算法智能出价(Auto-Bid)、智能调价(OCPX)等Bidding方式繁荣发展,混合竞价,预估大小准确性和稳定性直接影响出价;② 多物料混合:图文、直播、短视频等各类内容形态广告混合,不同物料上的预估水平参差不齐;③ 广告与推荐流量混排:广告和推荐(自然)内容有各自独立的打分逻辑,预估大小的量纲和分布统一是能够保证混排公平性和高效性的基础。所以,预估值大小的准确性在广告领域至关重要。校准技术的目标是:使用户行为的预估值尽可能逼近真实概率值。具体形式化表示如下,其中X为基础预估模型的输出空间(如预估点击率),Y为实际用户行为(如点击与否),f(x)为校准函数,f*为最优校准函数。在实际应用中,优化预估值大小准确性的同时,也会保证整体排序水平不会下降。
现有预估模型在预估值上的不确定性,导致在实际应用中缺乏可信度(trustworthiness)和可解释性(interpretability),会导致次优结果甚至错误决策的风险,校准技术最早在气象预报和医疗诊断领域被提出和应用,近几年进一步延伸到自动驾驶和计算广告领域。具体校准方法总的来讲可以分为两大类:第一类是尝试将导致模型预估偏差的因素(如假设分布偏差等各类先验信息)反向引入特征处理或损失函数中,端到端优化预估值大小。第二类是后处理方法(Post-processing),即在基础预估模型的基础上串接一个校准模块,以后处理的方式得到校准结果。这种方式更具灵活性,是目前研究和应用最为广泛的形式。常见的后处理校准方法包括:Histogram Binning(将样本分为多个桶,每个桶内的样本Label均值作为该桶每个样本的校准结果)、Isotonic Regression(学习一个保序函数作为校准函数,它能够保证校准后的结果和基础模型预估值的排序能力是一致的)以及Scaling方法(基于某种参数化分布函数学习预估值到校准值的映射)等。近几年,也发展出上述方法的结合算法,并对校准技术进行了理论验证,本文不做过多展开,详细可参考:https://github.com/huangsg1/uncertainty-calibration阿里妈妈的校准技术采用的是后处理方式,主要考虑以下两点原因:1.我们希望在不改变已有基础预估模型的前提下,将校准技术解耦,做成灵活可插拔的形式;2.端到端的方法难以快速响应线上分布的剧烈变化,在阿里大促活动中线上环境的频繁变化是常态,更需要具备轻便灵敏的模型校准能力。
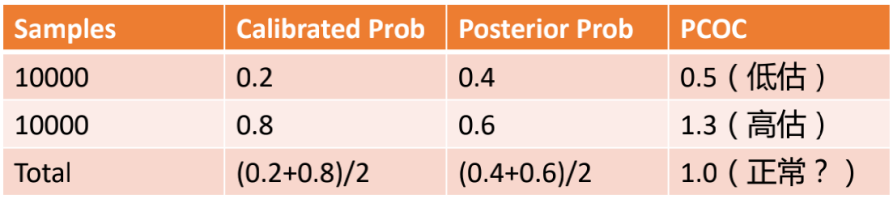
前面提到在实际环境中是无法观测到样本的真实点击概率的。但是我们可以采用近似的方法去逼近:针对观测样本,将各类特征相似的PV作为一个类簇,统计该类簇的整体点击率作为其中所有PV的真实点击概率(当类簇的数据量高于阈值时才认为是置信的);然后采用线性或非线性函数进行预估值和真实值的映射,该映射函数就构成了一种轻量级的校准函数。在这个过程中如何选择合理的类簇划分方式进行PV聚类就成为了问题的关键。经典的Isotonic Regression和Binning校准算法本质上是按预估值的大小进行样本划分,这种划分方式基于的假设是类簇划分精度的好坏与模型预估值的大小有关(或模型对于相近预估值大小的广告会具有相似的预估误差)。在实践中我们发现校准维度越精细,越有利于产出准确的校准函数,但同时样本量也变的稀疏,当数据量不具有统计意义时,反而会降低校准函数的准确度。所以算法设计中需要进一步权衡校准维度选择和数据稀疏的问题,我们的算法演进之路也是不断解决这两个问题的进化之路。在介绍校准算法之前,先介绍一下校准效果的度量指标。PCOC指标是校准之后的点击率与后验点击率(近似真实概率)的比值,越接近于1,意味着在绝对值上越准确,大于1为高估,小于1为低估,是一种常用的高低估评价指标。但是PCOC存在一定局限性,举个例子:2万个样本,其中1万个样本的预估概率是0.2,后验概率是0.4,计算出PCOC是0.2/0.4=0.5,是显著低估的,另1万个样本PCOC是0.8/0.6= 1.3,明显是高估的。所以校准效果并不好,但是样本放一起看,校准后概率是(0.2+0.8)/2=0.5,后验概率是(0.4+0.6)/2=0.5,整体PCOC是1.0,表现完全正常。所以单一PCOC指标不能表征样本各维度下的校准水平。针对PCOC问题,我们设计了一个新的指标Cal-N,将样本集合按照自定义规则划分出多个簇分别计算PCOC,并计算与标准1的偏差作为校准误差。相比PCOC,Cal-N显然能够更好的表征细粒度的校准水平。在广告领域中,通常会重点关注某一维度下的校准效果(如广告计划维度)。我们进一步提出了GC-N指标,能够在Cal-N基础上自定义各维度权重。以上是对校准背景、概念、相关工作以及评价方法的简单介绍。
从18年以来我们开始在校准算法上不断创新,实现了对点击率、转化率、收藏加购率、关注率等各类预估指标的校准能力。整个迭代路线以实际业务需求为导向,以轻量级、通用性和灵活性为设计目标。接下来详细介绍我们提出的各类校准方法。1. 保序回归平滑校准算法(Smoothed Isotonic Regression,SIR)
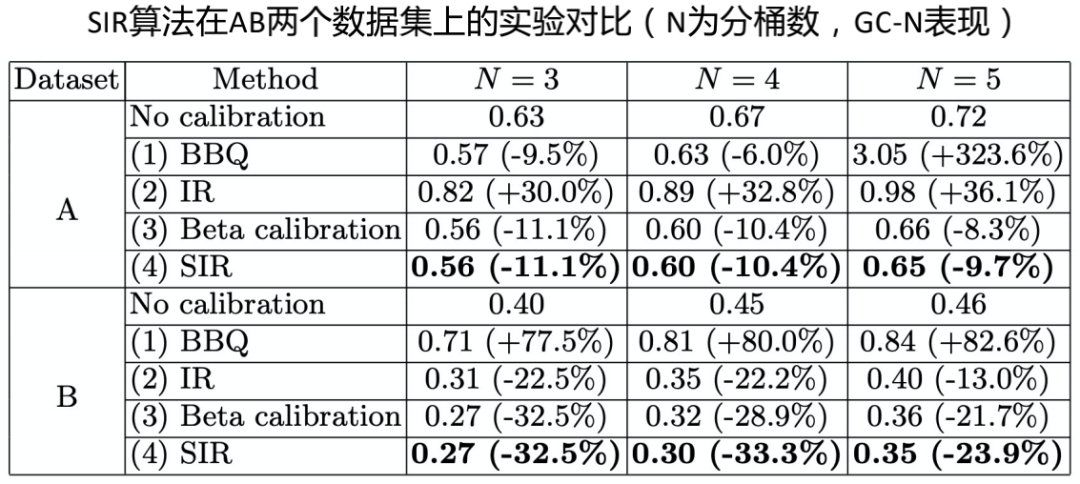
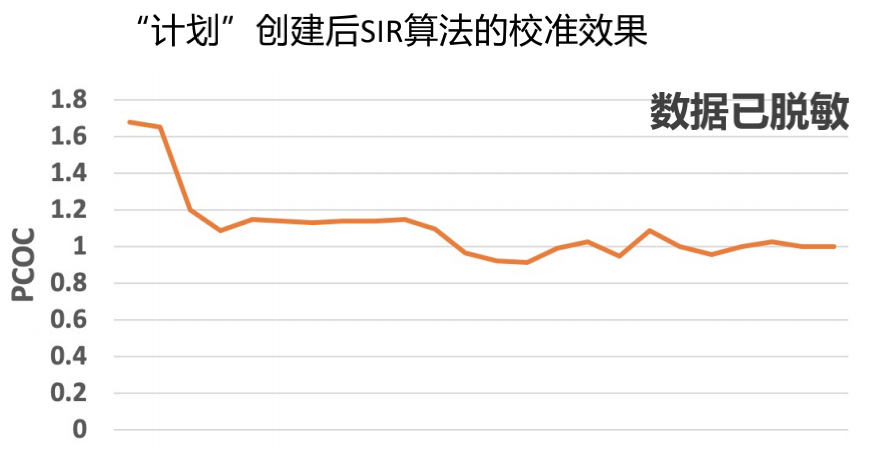
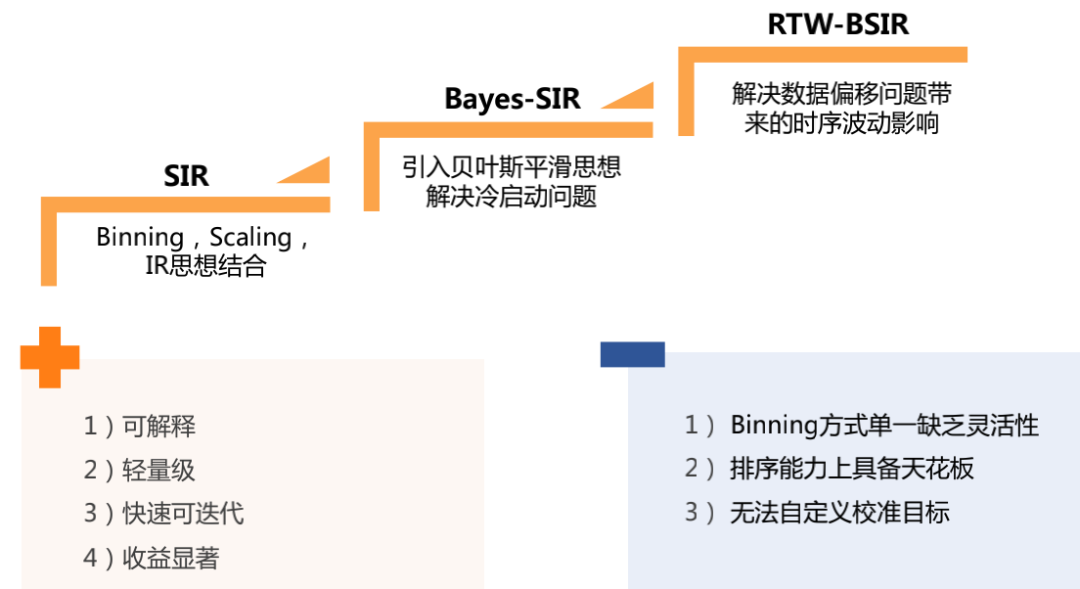
SIR算法是18年提出的,如上图所示,我们结合了Binning、Isotonic Regression和线性Scaling方法。具体思想为:模型原始打分相近的PV具有近似的真实点击率,PCTR大小区间可作为一个合理的校准维度(分桶);分桶数据量稀疏时,进一步利用模型本身的排序能力,对各分桶后验点击率与模型预估点击率做保序处理(保序回归);最后使用单调平滑函数拟合模型原始打分和后验点击率的映射关系(线性Scaling)就得到了校准函数。该算法的优势在于充分利用了保序和平滑思想缓解了数据稀疏的问题,而且具备轻量级和可解释性特点。对比各类校准算法效果如下(AB是两个数据集),在实际应用中RPM、CTR以及广告主ROI均有显著提升(详细可见论文:Calibrating user response predictions in online advertising)。
2. 贝叶斯平滑SIR校准算法(Bayes-SIR)
在SIR算法应用中,我们发现广告计划投放初期校准效果明显差于平均水平,并在实际业务中造成以下问题:1)影响新建计划初始阶段的投放表现;2)影响强时效性广告的全生命周期效果;3)小客户在整个投放周期里数据一直稀疏,得不到准确的校准,影响竞价公平性。这是SIR校准算法的冷启动问题,我们采用了Bayes平滑的思想进行优化(贝叶斯平滑方法最早在雅虎的一篇论文里面中提出,用于解决数据稀疏问题下的点击率预估优化)。
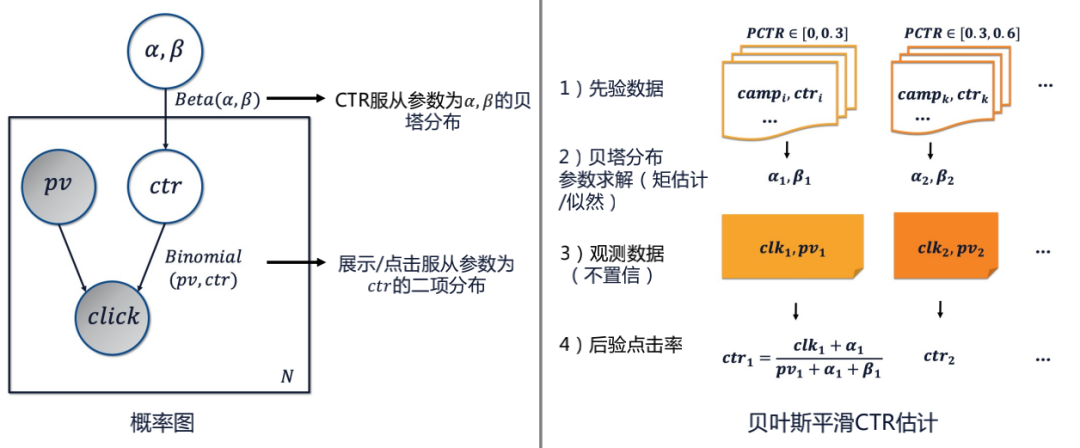
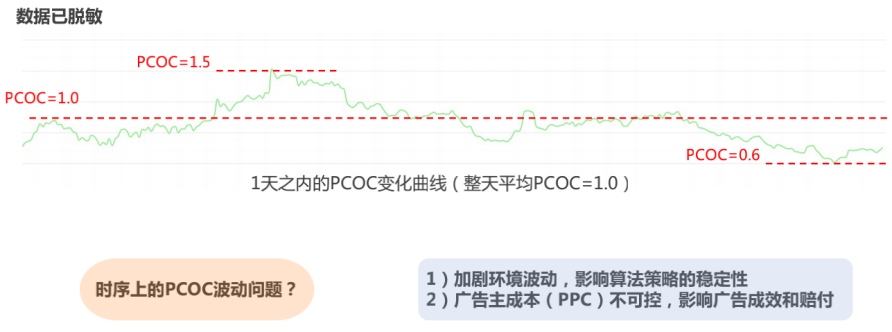
Bayes-SIR的算法思想:如上图所示,首先从丰富的先验数据中估计出每个广告计划的点击率先验分布,然后依据该先验知识和新观测到的少量数据,根据贝叶斯定理计算得到更准确的后验点击率。这种估计方法能充分利用先验知识,具备置信程度过渡平滑的特点。将贝叶斯平滑CTR估计过程替换掉SIR算法的朴素CTR统计逻辑即构成了具有冷启动问题优化效果的校准方法。实际上线后,新广告的投放效果得到明显的提升。3. Bayes-SIR实时波动问题优化(RTW-BSIR)实际应用中,我们进一步发现Bayes-SIR校准算法整体表现稳定,但是不同时间段内效果却是不断波动的,这会加剧广告竞价环境的波动,并影响广告计划拿量的均匀性和算法出价的稳定性(如上图所示)。
经分析,这是校准训练数据和应用时数据分布之间存在差异导致的,是一种典型的数据漂移问题。直接思路是将该差异进行消除,实现无偏的校准能力。考虑到时效性影响,数据分布一直在发生变化,如果直接对训练数据进行修正则无法避免后续模型训练链路延迟导致的偏差因素。所以我们借鉴了反事实学习的思想,通过实时计算应用数据和Bayes-SIR模型的分布偏差,直接修正Bayes-SIR校准函数,这样就实现了对现有校准效果时序波动性的优化算法(如下图所示)。上线应用后,能够有效保证校准效果的稳定性,尤其在大促活动等环境剧烈波动时,对流量分配效率极其稳定性起到明显的优化作用。上述内容介绍了SIR算法极其在冷启动和时序波动性方面的优化,该系列算法具备轻量级、可解释的特点,在阿里妈妈展示广告业务上得到了大范围的应用,并取得了非常显著的业务收益。
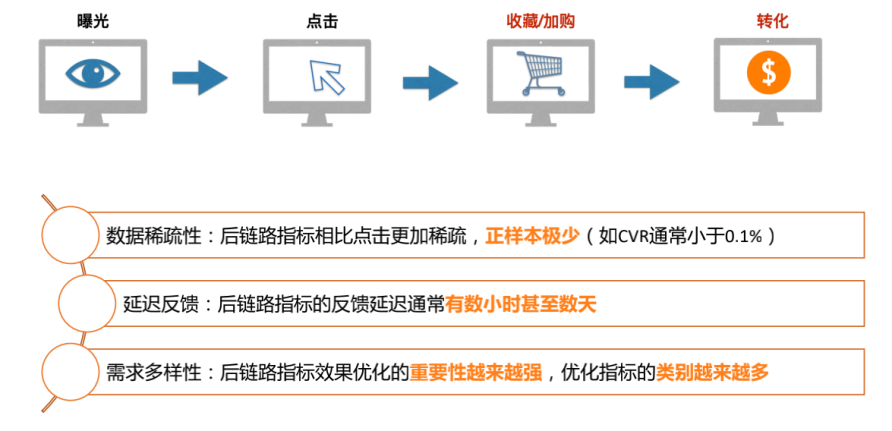
但是这些方法仍旧存在一些缺陷,比如Binning方式单一缺乏灵活性、排序能力上具备天花板而且无法自定义校准目标。针对这些问题我们也提出了新的算法方案,本文不再展开。下文进一步介绍校准算法在后链路指标校准方面的应用扩展。后链路指标指的是曝光/点击之后的加购、收藏、转化、关注等指标(特点如上图所示)。面向转化或加购等优化目标的算法出价能力不断成为主流的广告投放方式,但是转化和加购的模型预估能力远不如点击率,这使得后链路预估值的校准存在极大的必要性和可优化空间。相比点击率校准,后链路预估值的校准存在新的挑战:数据稀疏性和延迟反馈,以转化为例,用户点击广告后不一定立即产生购买行为,这导致我们无法实时计算准确的后验转化率以指导校准函数的训练,而等待多天后再产出校准函数,预估模型的分布也可能发生了新的变化。
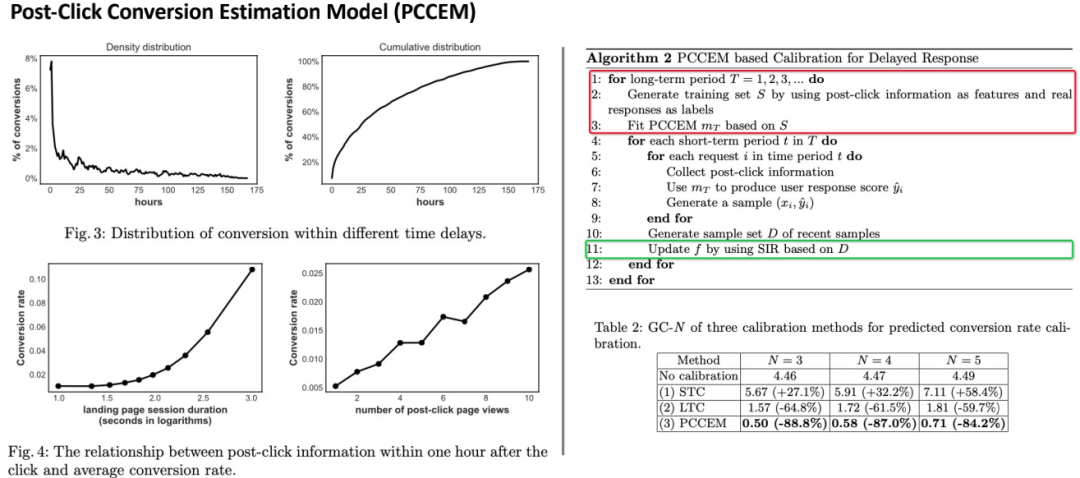
我们提出了一种算法叫Post-Click Conversion Estimation Model,简称PCCEM。上图左侧的折线图反映了转化的延迟性以及短期中间指标与转化行为的相关性。所以,针对延迟反馈问题,我们可以构建用户点击后的短期行为(如浏览、停留时长等)与后链路指标之间的关系来预测用户长期的转化行为,该模型被称为PCEEM模型。在该模型基础上,结合前述点击率的校准算法即可实现对后链路指标的校准能力(算法如上图右侧伪码所示,具体可参考论文:Calibrating user response predictions in online advertising)。在线上应用后广告转化率以及广告主ROI均有显著提升。
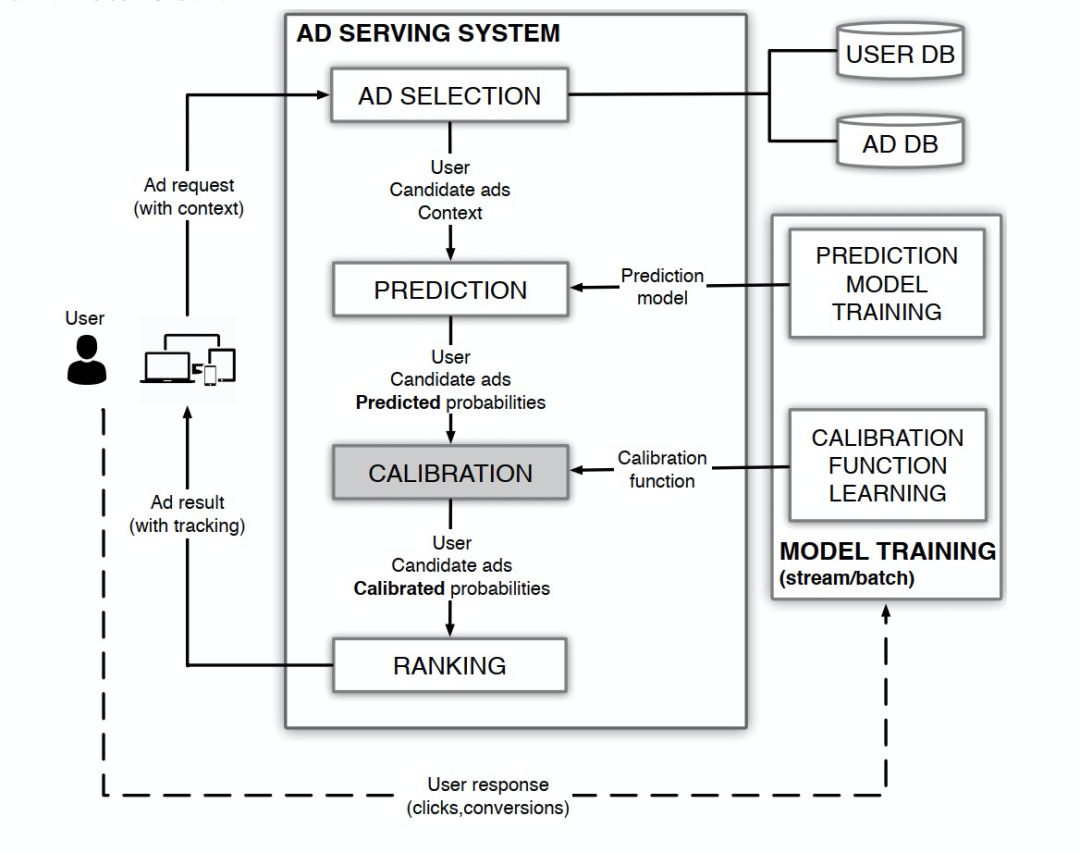
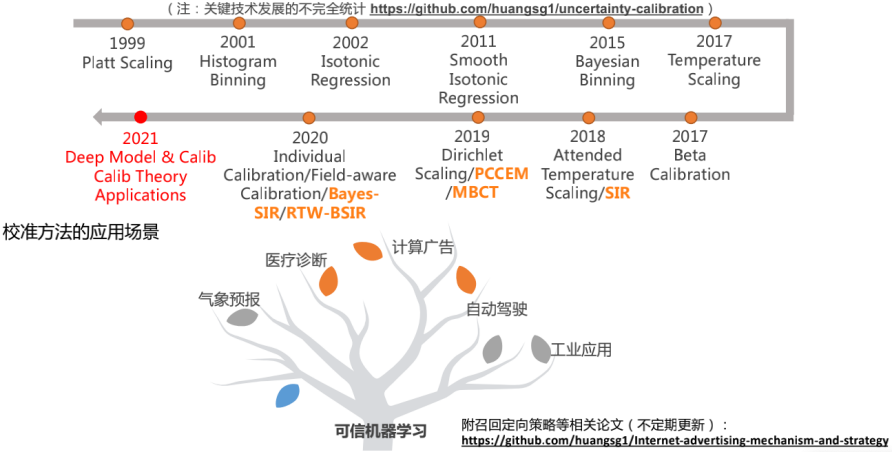
如上图所示,我们在实际应用中,Calibration模块在预估和策略排序模块之间,和其他模块是独立和解耦的,有利于校准的灵活性。2. SIR/PCCEM-Based算法数据流程图如上图所示,其中绿色部分是广告的召回排序预估链路,校准模块部分如果是浅层预估指标校准,直接基于Tracked Data,应用SIR系列校准算法即可完成校准;后链路指标则需要先进行点击质量预估(如蓝色区域),再进行算法校准。我们对校准技术做了详细的调研,上图中简要列了目前被广泛应用的校准算法,其中Platt Scaling方法早在1999年就被提了出来,后续也不断有别的方法被提出,但是一直到近几年才有计算机相关的论文从理论层面对校准技术进行证明和探讨(ICML/NIPS会议有相关文章)。阿里妈妈展示广告从18年开始在预估中引入校准方法,对广告系统的稳定性、效果的保障性以及算法出价能力等方面起到了显著的优化作用。但是过去几年中我们一直走轻量级的迭代方式,缺少一些向更复杂更精细化方法的探索,而且在发展过程中一直以业务需求为导向,在理论层面缺乏深入的探索,这些问题将是我们未来重点优化的方向。
校准技术在气象预报、医疗诊断、自动驾驶、计算广告以及工业应用等领域都有实际的落地应用。也有学者将校准技术归纳可信机器学习的一个研究分支,它可以为机器学习模型的确定性、可信度以及可解释性起到优化作用,辅助提升机器学习模型在各领域的实际应用价值。问:请问Bayes-SIR里面先验数据和观测数据的区别是什么?
答:先验数据是过去历史上所有能获取到的用户行为数据,也可能是专家经验。先验数据的粒度可以比较粗,范围可以比较大,时间也可以比较长,是对待校准数据表现的一个预判。观测数据是指待校准广告的即时表现,是短期的小部分可观测数据。答:有很多影响因素,特别是在广告系统中,除链路延迟外,广告主的行为以及用户习惯和兴趣都在不断发生变化,这些都会直接影响系统内数据分布的稳定性。问:校准模型是小时级更新的吗,还是天级更新就可以?答:因为基础预估模型的高低估程度在一天之内也在发生不断的波动,而且是不可预测的。所以校准模型理论上更新响应速度越快越好。答:窗口越短,模型反应越灵敏,但是数据量越稀疏,影响校准的准确性。在实际应用中会根据实际数据量级进行折中来确定窗口时长。答:可以。如果推荐系统的优化目标是绝对值效果(如绝对点击量,GMV等),排序策略中需要系统保证预估值大小的准确性,此时校准技术能够起到优化作用。问:SIR方法的分桶数量应该如何确定,有经验取值吗?答:这还是一个精细度和置信度权衡的问题。分桶数越多绝对值误差问题越能够被充分的暴露,校准效果也能做的越精细。但是桶内的样本量也就越少,统计上更不置信,影响校准结果的准确度。理论层面有一些对不同分桶数下的误差Bound的证明,在实际应用中是结合实验对比来确定的。编辑:王菁
校对:林亦霖