一道 Google 的面试题
大家好,我是一行
想进谷歌不会连这道题也不会吧
面试题目是这样的:
假设第1个杯子的容量是A升,第2个杯子的容量B升,两个杯子一开始都为空,现在有以下三种操作:
FILL(i):将 i 杯子中的水倒满。
DROP(i):将 i 杯子中的水全部倒出只剩空杯子。
POUR(i,j):将杯子 i 中的水倒到杯子 j 中,若杯子 j 满了或者杯子 i 已经为空了则停止。
如果你每次只能进行上面操作中的一种,如何使其中一个杯子的水容量恰好为C(C <= max(A,B))升?
问题入手分析:
当A=3, B=5, C=4 时,初始时两个杯子均为空,该如何操作?
很容易得出依次需要进行的操作为:
FILL(2),此时两个杯子的水容量为:0,5
POUR(2,1),此时两个杯子的水容量为:3,2
DROP(1),此时两个杯子的水容量为:0,2
POUR(2,1),此时两个杯子的水容量为:2,0
FILL(2),此时两个杯子的水容量为:2,5
POUR(2,1),此时两个杯子的水容量为:3,4
这就得到了容量为4的水。通过这个分析,我们能够得到哪些启发?
因为 i 和 j 的取值都是1或者2, 所以对于某个状态,所执行的操作总共有六种,下面会具体分析。
对于某一个状态,我们下面有 6 种选择,很明显,解决这类问题比较好的办法是广度优先遍历(BFS)。而广度优先遍历,所依赖的数据结构便是队列。
假设目前2个杯子水的容量分别为 a 和 b,那么可以执行的操作分别为:
1、FILL(1)
此时杯子1的水的容量变为A,而杯子2的水的容量不发生变化。
2、FILL(2)
此时杯子2的水的容量变为B,而杯子1的水的容量不发生变化。
3、DROP(1)
此时杯子1的水的容量变为0,而杯子2的水的容量不发生变化。
4、DROP(2)
此时杯子2的水的容量变为0,而杯子1的水的容量不发生变化。
5、POUR(1,2)
此种情况略微复杂,要分为两种场景:
1)、若杯子1中的水可以全部倒入杯子2中,即满足a<=B-b,那么杯子1的水的容量变为0,杯子2的水的容量变为a+b。
2)、若杯子1中的水倒入杯子2中还会有剩余,即a>B-b,那么杯子1的水的容量变为 a-(B-b),杯子2的水的容量变为B。
6、POUR(2,1)
此种情况同POUR(1,2),也要分为两种场景:
1)、若杯子2中的水可以全部倒入杯子1中,即满足b<=A-a,那么杯子2的水的容量变为0,杯子1的水的容量变为a+b。
2)、若杯子2中的水倒入杯子1中还会有剩余,即b>A-a,那么杯子2的水的容量变为 b-(A-a),杯子1的水的容量变为A。
所以,对于某个状态,我们需要广度优先遍历上述6种操作,当遇到某个杯子的容量为C时,停止广度优先遍历,遍历的过程可以用下图简单表示:
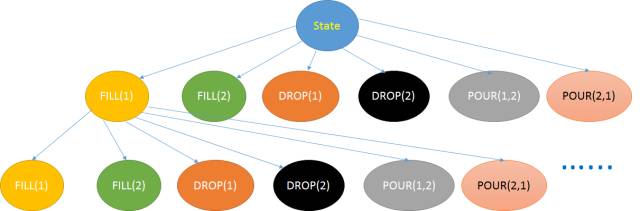
明白了上述原理,就可以考虑队列节点的数据结构了:
对于每个状态,我们需要存储的信息包括:当前杯子1的水的容量a,当前杯子2的水的容量b,由上个状态到本状态执行的操作,以及上一个状态的信息(需要由此获得所有的操作流程)。Python代码如下:
class Node:
# a:当前状态杯子1的水的容量
# b:当前状态杯子2的水的容量
# pre 上一个状态
# action上一个状态到本状态执行的操作
def __init__(self, a, b, pre, action):
self.a = a
self.b = b
self.pre = pre
self.action = action对于BFS,理解了上述6种操作就很简单了,在这里特别要注意的是避免死循环,所以在入队列的时候只入之前没出现过的状态,用数组visted 记录已经存在过的状态,存在过的状态就不入队列。Python代码如下:
def BFS(A, B, C):
"""
通过广度搜索来计算容量为C的水
:param A: 容量为A的杯子1
:param B: 容量为B的杯子2
:param C: 容量为C的水
:return:
"""
# visited 记录是否有过相关的容器组合,如果没有才塞入队列,避免死循环
maxC = max([A,B])
visited = [[0 for i in range(maxC + 1)] for i in range(maxC + 1)]
# 初始化队列
q = Queue.Queue()
# 初始化队列的第一个节点并放入队列
node = Node(0, 0, None, "0")
q.put(node)
while not q.empty():
cur = q.get()
# FILL(1)
a = A
b = cur.b
pre = cur
action = "FILL(1)"
if not visited[a][b]:
node = Node(a, b, pre, action)
q.put(node)
visited[a][b] = 1
if a == C or b == C:
return True, node
# FILL(2)
a = cur.a
b = B
pre = cur
action = "FILL(2)"
if not visited[a][b]:
node = Node(a, b, pre, action)
q.put(node)
visited[a][b] = 1
if a == C or b == C:
return True, node
# DROP(1)
a = 0
b = cur.b
pre = cur
action = "DROP(1)"
if not visited[a][b]:
node = Node(a, b, pre, action)
q.put(node)
visited[a][b] = 1
if a == C or b == C:
return True, node
# DROP(2)
a = cur.a
b = 0
pre = cur
action = "DROP(2)"
if not visited[a][b]:
node = Node(a, b, pre, action)
q.put(node)
visited[a][b] = 1
if a == C or b == C:
return True, node
# POUR(1,2)
if cur.a < B - cur.b:
a = 0
b = cur.b + cur.a
pre = cur
action = "POUR(1,2)"
else:
a = cur.a - (B - cur.b)
b = B
pre = cur
action = "POUR(1,2)"
if not visited[a][b]:
node = Node(a, b, pre, action)
q.put(node)
visited[a][b] = 1
if a == C or b == C:
return True, node
# POUR(2,1)
if cur.b < A - cur.a:
a = cur.b + cur.a
b = 0
pre = cur
action = "POUR(2,1)"
else:
a = A
b = cur.b - (A - cur.a)
pre = cur
action = "POUR(2,1)"
if not visited[a][b]:
node = Node(a, b, pre, action)
q.put(node)
visited[a][b] = 1
if a == C or b == C:
return True, node
return False, None还需要一个代码,获取一步步操作的流程,这里,由于拿到的是最后一个节点,所以要根据pre逆向寻找相关的action,并存储在列表中。最后,将结果逆向输出:
def ShowResult(node):
"""
根据最终节点选择前面的节点,并打印action
:param node:
:return:
"""
L = []
while node.pre is not None:
L.append(node.action)
node = node.pre
inverseL = L[::-1]
for item in inverseL:
print item有了上述代码,就可以设置不同的容量值来进行测试了:
if __name__ == '__main__':
A = 3
B = 5
C = 4
flag, node = BFS(A, B, C)
if flag is True:
ShowResult(node)
else:
print "Impossible"现在想想,一步步分析下来,题目就没有当初第一眼看到题目时那么难了吧?所以,当遇到难题时,一定要从小问题入手,逐步化解,由浅入深。
推荐阅读
(点击标题可跳转阅读)
转了吗 赞了吗 在看吗



