揭开数组的真面目
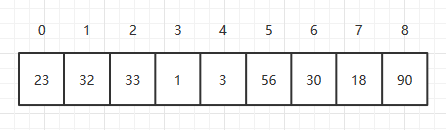
数组做为一种基础的数据存储结构,应用十分广泛。数组是用连续的内存空间来存储固定长度的、相同数据类型的一种数据结构。数据结构是跟语言无关的,这里,使用java来进行数组的相关操作。数组的索引是从0开始的。
一 数组初始化
创建数据有两种方式,一种是先声明一个固定长度的数据,然后再给数组赋值,另一种是直接赋值。
第一种:
数据类型[] 数组名称 = new 数据类型[长度];
这里的[]标识这声明了一个数组,这个[]除了可以放在数据类型后面,也可以放在数组名词后面,效果一样。假如我申明一个长度为2的long类型的数组,并赋值:
long[] arr = new long[2];
arr[0] = 1;
arr[1] = 2;
第二种:
数据类型[] 数组名称 = {元素1,元素2, ...};
这样在数组初始化的时候直接给数组赋值,数组的长度由元素的个数决定。
二 自定义类封装数组实现数据操作
public class MyArray {
// 自定义数组
private long[] arr;
// 有效数据长度
private int element;
public MyArray(){
arr = new long[9];
}
public MyArray(int maxsize){
arr = new long[maxsize];
}
/**
* 显示数组元素
*/
public void display(){
System.out.print("[");
for (int i = 0; i < element; i++) {
System.out.print(arr[i]+" ");
}
System.out.print("]");
}
}
2.1 添加元素
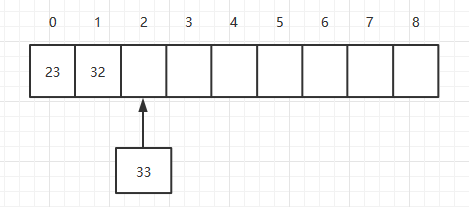
数组是用连续的内存空间来存储数据的,则每次添加的时候会往当前数组的最后一个元素上添加元素,一次就可以加上元素,所以它的复杂度为O(1),假如定义一个长度为9数组,数组中已经有两个元素,则添加第三个元素如下:
public void add(long value){
arr[element] = value;
element++;
}
2.2 根据值查询元素位置
这种查找方式也叫做线性查找,就是根据传入的值循环去遍历元素,来获取对应的位置,理论上平均查询一个元素需要花费N/2次,所以它的复杂度为O(N)。
public int find(long value){
int i;
for (i = 0; i < element; i++) {
if(value == arr[i]){
break;
}
}
if(i == element){
return -1;
}else {
return i;
}
}
2.3 根据索引查询元素
根据索引来查找元素,也就是获取对应位置的元素,其复杂度为O(1)。
public long get(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
return arr[index];
}
}
2.4 根据索引删除元素
删除对应索引的元素后,我们需要将所有改索引后面的元素,向前移动一位。假如我要删除索引为2的元素,如下:
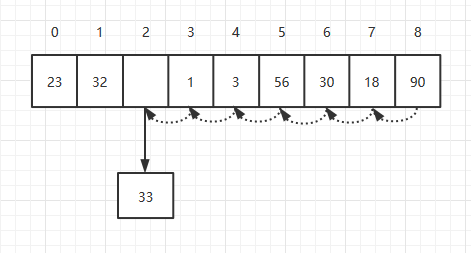
理论上平均删除一个元素,我们需要移动N/2次,所以它的复杂度也为O(N)。
public void delete(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
for (int i = index; i < element; i++) {
arr[index] = arr[index+1];
}
element --;
}
}
2.5 修改元素
修改某个位置的元素,直接根据索引就一次就可以修改对应的元素,所以它的复杂度为O(1)。
public void change(int index,long newValue){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
arr[index] = newValue;
}
}
三 有序数组
有序数组是数组的一种特殊类型,有序数组中的元素按照某种顺序进行排列。
3.1 添加元素
在添加元素的时候,将元素按顺序添加到某个位置。如下,在一个数组中添加一个33的元素。
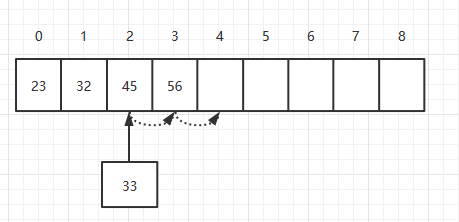
首先,将索引为3的元素移动到索引为4的位置,然后将索引为2的元素移动到索引为3的位置,最后将33添加到索引为2的位置。理论上插入一个元素需要移动元素的个数平均为N/2个,所以它的复杂度为O(N)。
public void add(long value){
int i;
for (i = 0; i < element; i++) {
if(arr[i]>value){
break;
}
}
for (int j = element; j > i; j--){
arr[j] = arr[j-1];
}
arr[i] = value;
element++;
}
3.2 二分法根据元素查询索引
在无序数组中,使用线性法进行查找相关元素,线性法即按索引按个查找。有序数组可以使用二分法来查找元素,二分法是指将一个数组从中间分成两个,判断元素位于哪个数组中,然后重复这样的操作。
假如有8个元素的一个数组,数组内容为有序的0-7的序列,要查找5这个元素,第一次分成0-3和4-7两个数组,然后再将4-7分成4-5和6-7两个数组,最后再将4-5分成4和5就查询出来具体的元素了,这样分割3次就可以查询出长度为8的数组中具体的元素,其复杂度即为O(logN)(logN在计算机中底数一般指的是2,意思为2的几次方等于n)。
public int search(long value){
// 中间值
int middle = 0;
// 最小值
int low = 0;
// 最大值
int pow = element;
while (true){
middle = (low + pow) / 2;
if(arr[middle] == value){
return middle;
}else if (low > pow){
return -1;
}else{
if(arr[middle] > value){
pow = middle - 1;
}else{
low = middle + 1;
}
}
}
}
四 总结
复杂度越低意味着算法更加优秀,所以O(1) > O(logN) > O(N) > O(N^2)。
| 算法 | 复杂度 |
|---|---|
| 线性查找 | O(N) |
| 二分法查找 | O(logN) |
| 无序数组插入 | O(1) |
| 有序数组插入 | O(N) |
| 无序数组删除 | O(N) |
| 有序数组删除 | O(N) |
无序数组插入快,查找和删除慢
有序数组查找快,插入和删除慢
