关于二分查找,我有话说
前言
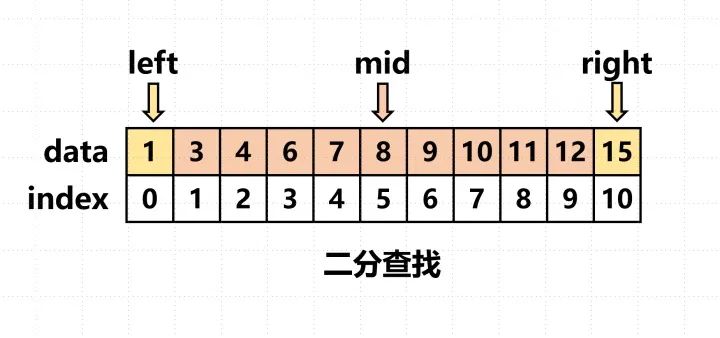
最基础版二分法
public static int commonBinarySearch(int[] arr, int target) {
int left = 0, right = arr.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(arr[mid] == target) {
return mid;
}
if(arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}进阶版
public static int firstBinarySearch(int[] arr, int target) {
int left = 0, right = arr.length - 1;
int res = -1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(arr[mid] == target) {
res = mid;
right = mid - 1;
} else if(arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return res;
}public static int lastBinarySearch(int[] arr, int target) {
int left = 0, right = arr.length - 1;
int res = -1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(arr[mid] == target) {
res = mid;
left = mid + 1;
} else if(arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return res;
}public static int lowerBiggest(int[] arr, int target) {
int left = 0, right = arr.length - 1;
int res = -1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(arr[mid] < target) {
res = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return res;
}public static int higherSmallest(int[] arr, int target) {
int left = 0, right = arr.length - 1;
int res = -1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(arr[mid] <= target) {
left = mid + 1;
} else {
res = mid;
right = mid - 1;
}
}
return res;
}题外话
练习题
评论
