[012] 不同数据集划分与验证方法的实现与比较

“哈哈,我们在训练我们的模型并且希望得到更加准确的结果,但基于实际的情况(比如算力、时间),往往会按照一定策略来选择。本文介绍了几种常见的数据集划分与交叉验证的方法策略以及它们的优缺点,主要包括了Train-test-split、k-fold cross-validation、Leave One Out Cross-validation等,包括了代码层的实现与效果的比较,比较适合综合阅读一次。
What is Model evaluation?
Model evaluation is a set of procedures allowing you to pick the best possible stable model. It is an essential part of the model development process. It reveals the model’s behavior and its predictive power — indicates the balance between bias and variance on unseen data. As a starting point, split the given dataset into a train and test set. The model will learn to predict using the train set; in comparison, we will utilize the test set to assess the model’s performance.
Train-test split k-fold cross-validation, K-Fold Leave One Out Cross-validation, LOOCV
Methods used for splitting
There are different strategies to split the data and make sure that it is done fairly taking into consideration the special characteristics the attributes could have. For example, you could have biased predictions if the original data has an imbalance between features, so for each case, a specific method might be recommended.
The main methods that would be covered in this article are as the following:
Train-test split k-fold cross-validation, K-Fold Leave One Out Cross-validation, LOOCV
Train test split
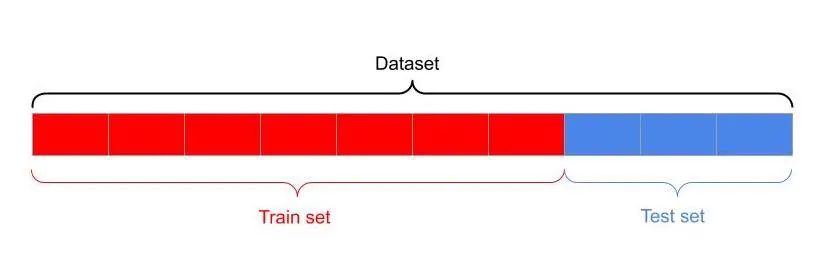
regular train-test split using sklearn — image by the author
It is a way to split the dataset into two halves with a specific percentage. It is easy and quick. It might be appropriate to use when comparing different algorithms to decide which one you might consider.
The train_test_split method within the sklearn. model_selection module is widely utilized to split the original dataset. A common split ratio is 80/20 or 70/30.
“You can split the training set into train and validation set with the same split ratio above — Stackoverflow discussion
I did use stratify here because the original dataset has an imbalance in the target class — 500/268.
# set the seed to keep code reducibility
seed = 7# Apply the splitting
x_train, x_test, y_train, y_test = train_test_split(
X, y,
test_size = 0.33,
stratify = y, #to keep class balance during splitting
random_state = seed
)
model = LogisticRegression(max_iter=1000)
model.fit(x_train, y_train)
result = model.score(x_test, y_test)
print(f'accuracy is: {result*100.0: 0.3f}')
“The resulted accuracy is: 76.378
Pros:
Easy to implement Quick execution, less computation time
Cons:
Inaccurate accuracy if the split is not random Might be a cause for underfitting if the original dataset has limited data points.
K-fold cross-validation
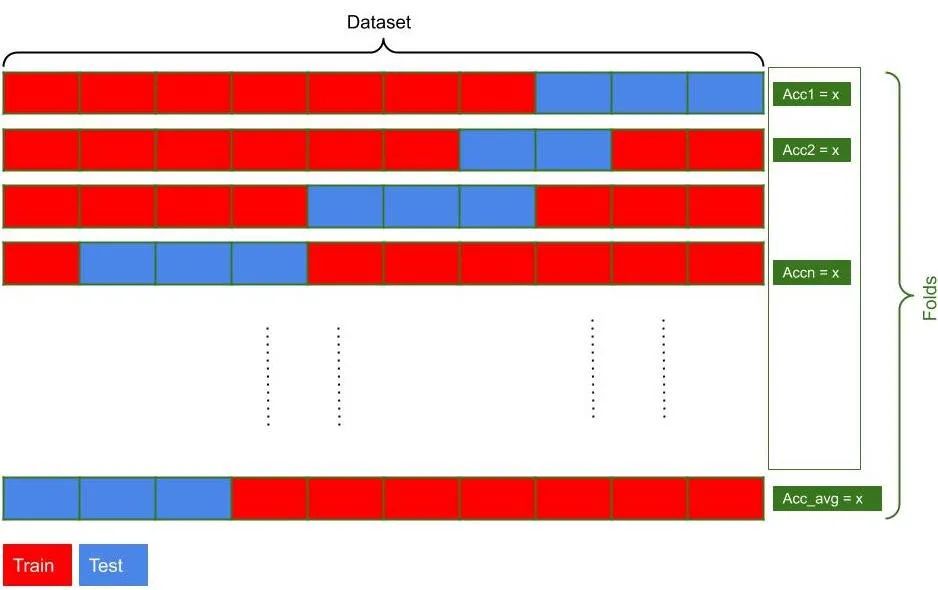
k-fold split procedure — image by the author
To enhance the model accuracy and avoid the regular split of the data disadvantages, we need to add more generalization to the split process. In this strategy, we are repeating the train_test_split multiple times randomly. For each split or fold, the accuracy is calculated then the algorithm aggregate the accuracies calculated from each split and averages them. That way, all the dataset points are involving in measuring the model accuracy, which is better.
For this example, we will use the RepeatedStratifiedKFold() within the sklearn library to assess the model since it repeats stratified folds n-times with a different random scheme in each iteration.
from sklearn.model_selection import RepeatedStratifiedKFold
from scipy.stats import sem
import numpy as np
import matplotlib.pyplot as pltcv_repeated = RepeatedStratifiedKFold(
n_splits = 10,
n_repeats = 16,
random_state = seed
)scores_r = cross_val_score(
model,
X, y,
scoring = 'accuracy',
cv = cv_repeated,
n_jobs = -1
)print('Accuracy: %.3f (%.3f)' % (scores_r.mean(), scores_r.std())))
“The resulted accuracy is: 0.775 (0.042)
Accessing the model accuracies across each fold
It is a good idea to investigate more on the distribution of the estimates for better judgments.
# evaluate a model with a given number of repeats
def asses_model(X, y, repeats):
# define the cv folds
cv = RepeatedStratifiedKFold(
n_splits=10,
n_repeats=repeats,
random_state = seed)
# create the model
model = LogisticRegression(max_iter=1000)
# evaluate model
scores = cross_val_score(
model,
X, y,
scoring = 'accuracy',
cv = cv,
n_jobs=-1)
return scores
Then we will use the sem() method from the scipy library to calculate the standard error for each sample.
repeats = range(1, 16)
res = list()
for rep in repeats:
scores = asses_model(X, y, rep)
print('Sample_%d mean=%.4f se=%.3f' % (rep, np.mean(scores), sem(scores)))
res.append(scores)

Let’s visualize the samples accuracies with a boxplot to better understand the results

accuracy across splits — image by the author
The orange line represents the median of the distribution of the accuracy while the green triangle indicates the arithmetic mean.
As demonstrated in the graph above, the model accuracy stabilizes around 6 and 7, which is the number of folds to harness (0.775 (0.042) accuracy).
Pros:
Higher accuracy Handles class imbalances better. less probability of underfitting
cons:
More prone to overfitting, so we need to monitor the accuracies across folds. High computational power and more execution time.
Leave-One-Out Cross-validation
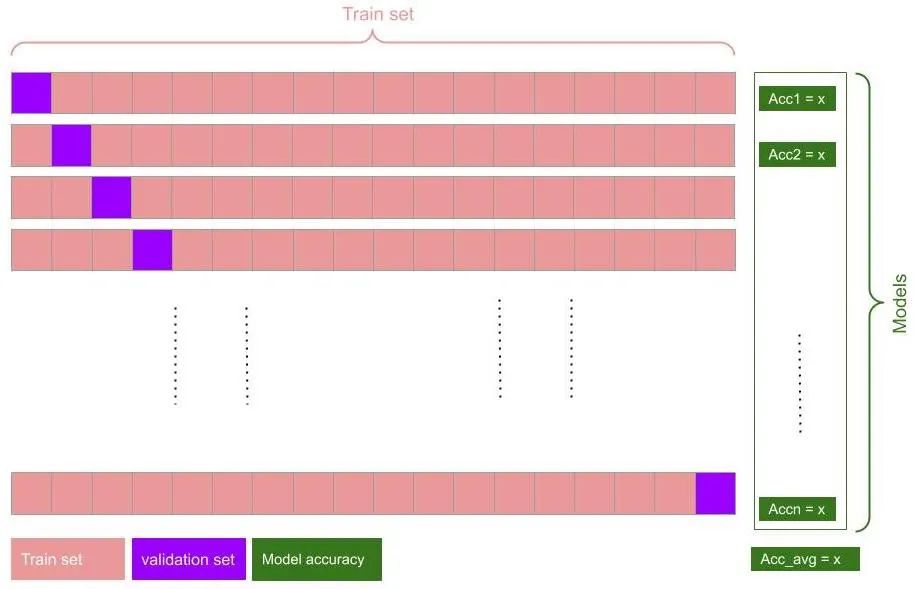
leave one out cross-validation — image by the author
In this strategy, The algorithm picks a data point for each training fold and excludes it while model training. The validation set hence used to calculate the model the accuracy; then repeat this process for each training fold. The final accuracy has been calculated after averaging each fold accuracy.
“In this strategy, we create n-1 models for n observations in the data.
from sklearn.model_selection import LeaveOneOut
loocv = LeaveOneOut()
model = LogisticRegression(max_iter=1000)
res = cross_val_score(model, X, y, cv = loocv)
print('Accuracy: %.3f (%.3f)' % (np.mean(res), np.std(res)))
“The resulted accuracy is: 0.776 (0.417)
Pros:
Very efficient if the dataset is limited — since we want to use as much training data as possible when fitting the model. It has the best error estimate possible for a single new data point.
cons:
Computationally expensive. If the dataset is large in size. If testing a lot of different parameter sets.
The best way to test whether to use LOOCV or not is to run KFold-CV with a large k value — consider 25 or 50, and gauge how long it would take to train the model.
Takeaways and Closing notes
We explored the most common strategies to train the model in machine learning effectively. Each method has its pros and cons; however, there are some tips that we may consider when choosing one.
K-fold cross-validation is a rule of thumb for comparing different algorithms’ performance — most k-fold is 3, 5, and 10. Start with the regular train test split to have a ground truth of a specific algorithm’s estimated performance. Leave one out cross-validation — LOOCV is a deterministic estimation, where there is no sampling on the training dataset. On the other hand, other strategies follow a stochastic estimate. LOOCV might be appropriate when you need an accurate estimate of the performance.
