斐波那契数列-爬楼梯算法

爬楼梯算法

有n级楼梯，有2种爬法，1次1级，或1次2级，问，n级楼梯有多少种爬法？

递归求解

首先，当只有一阶楼梯的时候，很显然只有一种走法；有两阶楼梯的时候，也很显然的知道有两种走法。就会有下面这句判断语句。

if (n == 1 || n == 2) {  return n}

一阶二阶的思想就出来了，那如果当阶数是三阶四阶甚至n阶的时候呢?

当 n > 2 时，第一次跳一级还是两级，决定了后面剩下的台阶的跳法数目的不同：如果第一次只跳一级，则后面剩下的 n-1 级台阶的跳法数目为 f(n-1)；如果第一次跳两级，则后面剩下的n-2 级台阶的跳法数目为 f(n-2)。所以，得出递归方程，f(n) = f(n-1) + f(n-2)。问题本质是斐波那契数列。

聊着聊着我们的代码就出来了。

var climbStairs = function (n) {  if (n == 1 || n == 2) {    return n  }  else {    return climbStairs(n - 2) + climbStairs(n - 1)  }}

斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）

我们现在回到兔子问题。

假设一对初生兔子要一个月才到成熟期，而一对成熟兔子每月会生一对兔子，那么，由一对初生兔子开始，12 个月后会有多少对兔子呢？

我们按照规则，画出了1-7月份兔子的繁殖情况。我们发现1-7月份兔子的数量分别为1, 1, 2, 3, 5, 8, 13对。为了更清晰一点，我们作出下面的示意图。

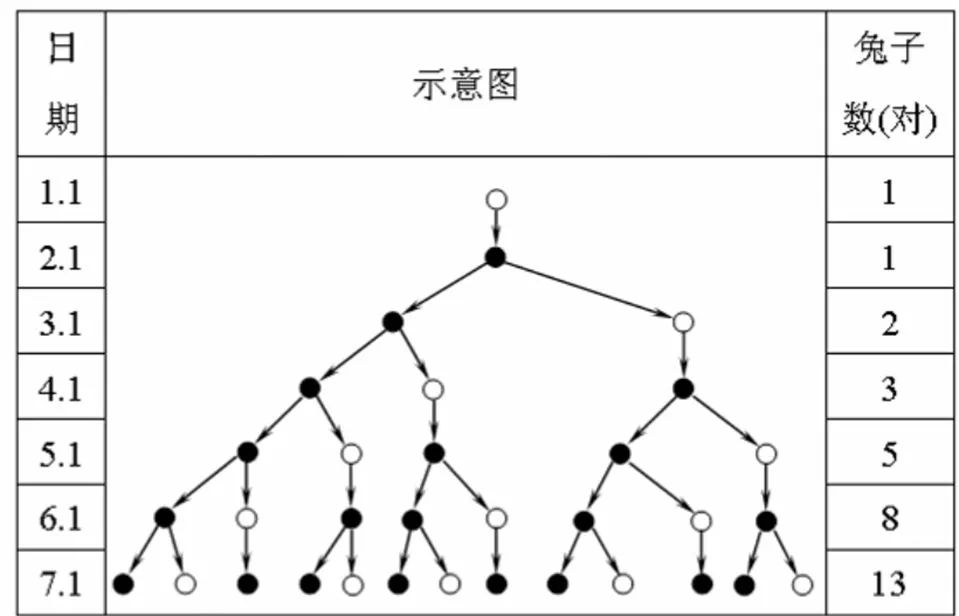
显然在图中，我们的黑点表示的是成熟兔子，白点表示的是小兔子。我们够仔细的话能够发现，右边这一列数字是有规律的。第一个数和第二个数为1，之后的每一个数为之前两个数之和。比如，六月份的兔子数量为四月份和五月份兔子数量之和，即8=5+3。

var climbStairs = function (n) {  if (n == 1 || n == 2) {    return 1  }  else {    return climbStairs(n - 2) + climbStairs(n - 1)  }}

因此，兔子问题得以解决，答案为144对。以上数列，即“斐波那契数列”。

总结

斐波那契数列的自身特性：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

第一项和第二项是1，之后的每一项为之前两项的和。即：

a1=a2=1

an=an-1+an-2 （n为正整数）