“

第一篇关于「栈与队列与链表篇」 的文章不知道大家有没有学习完哈，在正式进入「递归与回溯篇」前，我们先来一点热身题，然后刷一刷前置知识，希望大家跟进脚步，一起加油，努力变优秀~

”

热身题

面试题 16.11. 跳水板

「题目描述」

你正在使用一堆木板建造跳水板。有两种类型的木板，其中长度较短的木板长度为shorter，长度较长的木板长度为longer。

你必须正好使用k块木板。编写一个方法，生成跳水板所有可能的长度。

返回的长度需要从小到大排列。

示例 1

输入：
shorter = 1
longer = 2

k = 3
输出： [3,4,5,6]
解释：
可以使用 3 次 shorter，得到结果 3；使用 2 次 shorter 和 1 次 longer，得到结果 4 。以此类推，得到最终结果。

提示：

0 < shorter <= longer
0 <= k <= 100000

「解题思路」

排列组合也算比较简单，需要 k 个板子，当我们短板有 i 个的时候，长板子就是 k-i 个，由于题目要求是将结果从小到大进行排序，那么我们起初就尽可能多的取短板子，最后结果就是通过 [0,k] 范围内遍历一遍即可。

对于特殊情况，即短板和长板长度相同时，我们只需要返回 k*len 即可，不然会重复计算。

var divingBoard = function(shorter, longer, k) {
    if(k===0) return []
    if(shorter === longer) return [k*shorter]
    let res = []
    for(let i=k;i>=0;i--){
        let shortCnt = i
        let longCnt = k-i
        let cnt = shortCnt*shorter + longCnt*longer
        res.push(cnt)
    }
    return res
};

1291. 顺次数

「题目描述」

我们定义「顺次数」为：每一位上的数字都比前一位上的数字大 1 的整数。

请你返回由 [low, high] 范围内所有顺次数组成的 有序 列表（从小到大排序）。

示例 1：

输出：low = 100, high = 300
输出：[123,234]

示例 2：

输出：low = 1000, high = 13000
输出：[1234,2345,3456,4567,5678,6789,12345]
 

提示：

10 <= low <= high <= 10^9

「解题思路」

「顺次数」为：每一位上的数字都比前一位上的数字大 1 的整数。

也就是例如 1234这样的数字，然后给你一段区间确定范围。

官方给了枚举方式，反正数据量也不是很大，但是我觉得还是有很多数字没必要枚举，可以直接剪枝掉。我的做法是先求出最小值和最大值对应字符串的长度，即求出我们能枚举的数字的长度范围。

然后我们的起点的最小值从 1 开始，起点的最大值从 10-len 开始。为什么是 10-len？举例说明，示例1给的是 [100,300]范围的值，那么可枚举的长度 len 为 3，起点的最大值就位 10 - 3 = 7。那么此时顺次数为 789 但是不在我们区间范围内，舍弃。然后8、9开头的数字就不需要枚举了。这样，我们就能剪掉一部门数据了。（虽然暴力是永远滴神...）

/**
 * @param {number} low
 * @param {number} high
 * @return {number[]}
 */
var sequentialDigits = function(low, high) {
    let res = []
    let lowLen = low.toString().length
    let highLen = high.toString().length
    for(let i=lowLen;i<=highLen;i++){
        for(let j=1;j<=10-i;j++){
            let str = ''
            let num = j
            str += num
            let k = i-1
            while(k--){
                num++
                str += num
            }
            let ans = parseInt(str)
            if(ans>=low && ans<=high){
                res.push(ans)
            }
        }
    }
    return res    
};

矩阵

73. 矩阵置零

「题目描述」

给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。请使用原地算法。

示例 1:

输入: 
[
  [1,1,1],
  [1,0,1],
  [1,1,1]
]
输出: 
[
  [1,0,1],
  [0,0,0],
  [1,0,1]
]

示例 2:

输入: 
[
  [0,1,2,0],
  [3,4,5,2],
  [1,3,1,5]
]
输出: 
[
  [0,0,0,0],
  [0,4,5,0],
  [0,3,1,0]
]

进阶:

一个直接的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个常数空间的解决方案吗？

「解题思路」

用 O(n) 空间复杂度来做，先遍历矩阵，找到等于0的坐标，然后遍历坐标，将对应行和列置为 0 即可

时间复杂度 O(m * n)

var setZeroes = function(matrix) {
    let n = matrix.length
    let m = matrix[0].length
    let arr = []
    for(let i=0;i<n;i++){
        for(let j=0;j<m;j++){
            if(matrix[i][j] == 0){
                arr.push([i,j])
            }
        }
    }
    while(arr.length){
        let [x,y] = arr.pop()
        for(let i=0;i<n;i++) matrix[i][y] = 0
        for(let j=0;j<m;j++) matrix[x][j] = 0
    }
    return matrix
};

另外一种，「原地算法」，空间复杂度 O(1)，我们无需借助外部空间。找到下标为 0 的坐标，然后直接对该行和该列不等于 0 的数字设置为 -0 即可。这里巧妙运用了 JS 中的 Object.is()方法，此时 0 和-0 不相等，但是最终返回的矩阵还是为 0

var setZeroes = function(matrix) {
    for(let i=0;i<matrix.length;i++){
        for(let j=0;j<matrix[0].length;j++){
            if(Object.is(matrix[i][j],0)){
                // 对行进行操作
                for(let k=0;k<matrix.length;k++)
                    if(!Object.is(matrix[k][j],0) && k!==i) matrix[k][j] = -0
                // 对列进行操作
                for(let k=0;k<matrix[0].length;k++)
                    if(!Object.is(matrix[i][k],0) && k!==j) matrix[i][k] = -0
            }
        }
    }
    return matrix
};

54. 螺旋矩阵

「题目描述」

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1:

输入:
[
 [1,2,3],
 [4,5,6],
 [7,8,9]
]
输出: [1,2,3,6,9,8,7,4,5]

示例 1:

输入:
[
 [1,2,3,4],
 [5,6,7,8],
 [9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]

「解题思路」

和「上一期」 螺旋矩阵差不多，这个是让我么输出，而上次是让我们构造，还是按照螺旋矩阵模拟即可，先从左到右，在从上到下，再从右到左，再从下到上。

不过这里的矩阵行和列不相同了，可能会出现不成环的情况，那么最后会留一列或一行出来，这里借用「大佬」一张图：

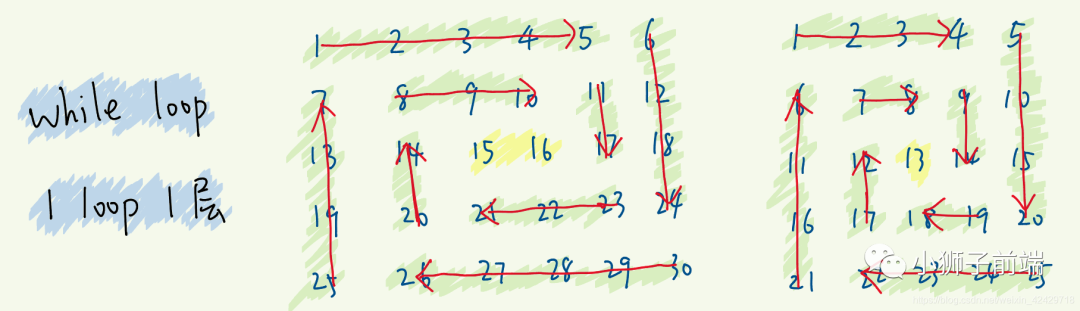
然后我们需要提前跳出去一下，就是避免重复计算，总数够了直接跳出去。注意下面代码 break。只能放在那里，因为遍历顺序，如果最后留下一行的话，需要从左到右遍历，此时 top > bottom  。如果最后留下一列的话，需要从上到下遍历，此时 left > right。

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function(matrix) {
    if(!matrix.length) return []
    let n = matrix.length
    let m = matrix[0].length
    let total = n*m
    let top = 0,bottom = n-1
    let left = 0,right = m-1
    let res = []
    while(res.length < total){
        for(let i=left;i<=right;i++) res.push(matrix[top][i]) // 从左到右
        top++
        for(let i=top;i<=bottom;i++) res.push(matrix[i][right]) // 从上到下
        right--
        /* 因为n 和 m 不相同的时候，最后可能会留一列或一行，避免重复计算，总数够了直接跳出去 */
        if(res.length === total) break
        for(let i=right;i>=left;i--) res.push(matrix[bottom][i]) // 从右到左
        bottom--
        for(let i=bottom;i>=top;i--) res.push(matrix[i][left]) // 从下到上
        left++
    }
    return res
};

59. 螺旋矩阵 II

「题目描述」

给定一个正整数 n，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:

「解题思路」

按照螺旋矩阵模拟即可，先从左到右，在从上到下，再从右到左，再从下到上。

每次进行cur++操作，直到累加到total为止。最后返回二维数组即可（没想到 js二维数组也是这样方便...）

/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function(n) {
    let top = 0, bottom =n-1
    let left = 0, right = n-1
    let res = []
    for(let i=0;i<n;i++) res[i] = []
    let cur = 1, total = n*n
    while(cur<=total){
        for(let i=left;i<=right;i++) res[top][i] = cur++  // 从左到右
        top++
        for(let i=top;i<=bottom;i++) res[i][right] = cur++ // 从上到下
        right--
        for(let i=right;i>=left;i--) res[bottom][i] = cur++ // 从右到左
        bottom--
        for(let i=bottom;i>=top;i--) res[i][left] = cur++ // 从下到上
        left++
    }
    return res
};

子集

46. 全排列

「题目描述」

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

「解题思路」

序列不重复就很简单了，维护一个 vis数组，不重复取就好了。

var permute = function (nums) {
  let res = [];
  let vis = {};
  let dfs = (t) => {
    if (t.length == nums.length) {
      res.push(t);
    }
    for (let i = 0; i < nums.length; i++) {
      if (vis[i]) continue;
      vis[i] = true;
      t.push(nums[i]);
      dfs(t.slice());
      t.pop();
      vis[i] = false;
    }
  }
  dfs([]);
  return res;
};

47. 全排列 II

「题目描述」

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

「解题思路」

本题是求全排列，并且排列不能重复。我们用一个 vis数组维护一下，让每一条路线保证不重复选取元素，而对于每一层而言，需要判断相邻元素是否相同，相同的就没必要走了，例如下图中红色三角形部分。

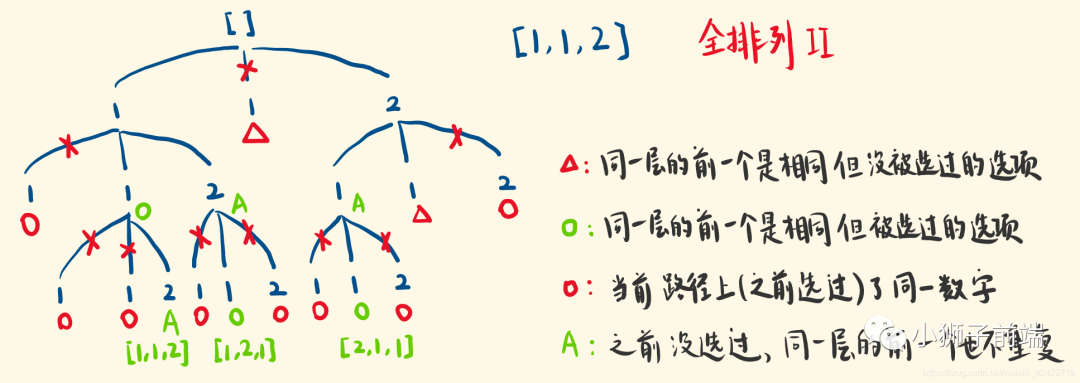
果当前的选项 nums[i] ，与同一层的上一个选项 nums[i - 1] 相同，且 nums[i - 1]有意义（即索引 >= 0），且没有被使用过，那就跳过该选项。

因为 nums[i - 1]如果被使用过，它会被修剪掉，不是一个选项了，即便它和 nums[i]重复，nums[i]还是可以选的。

「参考xiao_ben_zhu大佬题解」

var permuteUnique = function(nums) {
    let res = [];
    nums.sort((a,b) => a-b);
    let vis = {};
    let dfs = (t) => {
      if(t.length === nums.length){
        res.push(t);
      }
      for(let i=0;i<nums.length;i++){
        if(i-1>=0 && nums[i] == nums[i-1] && !vis[i-1]) continue;
        if(vis[i]) continue;
        vis[i] = true;
        t.push(nums[i]);
        dfs(t.slice(),i+1);
        t.pop();
        vis[i] = false;
      }
    }
    dfs([],0);
    return res;
};

78. 子集

「题目描述」

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

「解题思路」

一道组合相关的题目，采用回溯来做即可，题目说明不包含重复元素，于是我们也无需排序然后判断相邻元素是否相等来去重了。

var subsets = function(nums) {
  let res = [];
  let dfs = (t,start) => {
    res.push(t);
    for(let i=start;i<nums.length;i++){
      t.push(nums[i]);
      dfs(t.slice(),i+1);
      t.pop();
    }
  }
  dfs([],0);
  return res;
};

90. 子集 II

「题目描述」

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出:
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

「解题思路」

本题还是挺有意思的，我们要求的是子集，但是子集要进行去重操作，采用的做法是先对原数组进行排序，那么排序后的数组重复的元素必定是相邻的，然后在遍历解空间树的时候，要做一个去重的操作，当遇到重复出现，也就是和前面相邻元素相同的时候，直接跳过该节点，不让它向下递归。具体示意图如下：

「参考大佬题解」

dfs的话，一条路会一直走下去，然后回溯回来，在走之前，start是当前层第一个元素，只有当前元素下标大于 start才会有重复元素，而对于不同层的重复元素，我们不应该切断，应该继续走，不然就不会有 [1,2,2]这样的子集出现了。

var subsetsWithDup = function(nums) {
  let res = [];
  nums.sort((a,b)=>a-b);
  let dfs = (t,start) => {
    res.push(t);
    for(let i=start;i<nums.length;i++){
      // 同层重复，跳过
      if(i>start && nums[i-1] == nums[i]) continue;
      t.push(nums[i]);
      dfs(t.slice(),i+1);
      t.pop();
    }
  }
  dfs([],0);
  return res;
};

本文参考

• 「前端该如何准备数据结构和算法？」
• 「写给前端的算法进阶指南，我是如何两个月零基础刷200题」
• 「(1.8w字)负重前行，前端工程师如何系统练习数据结构和算法？【上】」

参考链接：

结语

❤️关注+点赞+收藏+评论+转发❤️，原创不易，您的支持将会是我最大的动力~

祝愿在准备春秋招の你，能够早点结束，offer 拿到手软，希望我的文章能够帮助到你，我们很快会在下期相遇，给个赞及时催更呀~

学如逆水行舟，不进则退