移动矩阵的问题求解方法
题目介绍
最近练题的过程中,遇到这么一种情况:在一个二维矩阵中,有一个小的固定的图形,需要移动这个小的图形到达某个指定的位置,求最短距离。
图形化的题目看起来长下面这个样子:
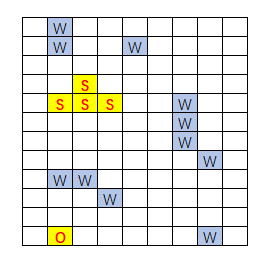
其中:
• S:表示起始位置
• O:表示目标位置,
S接触到O为终止条件• W:表示水域,是不可通过的区域
这个图还没看明白题目的话,不要紧。看下面这张图!!!

对滴!就是90坦克大战的简易版(暴露年龄,哈哈~),只不过我们题目的设定没那么复杂,坦克也不能转向。 下面就来看看代码吧!
代码实现
以下代码仅表述核心算法逻辑,请忽略变量初始化等问题哈~
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
/**
* 在一个二维矩阵中移动固定图案(一个小的矩阵,即多个元素的组合,其两两之间的相对位置不变)
* 求其到位某个满足条件位置的最小距离解法
*/
public class MoveArray {
// 矩阵规模,R行C列
static int R, C;
// 矩阵地图
static char[][] MAP;
// 待移动的图形的点的集合
static List<int[]> BODY;
// 上下左右移动的偏移量
static int[][] MOVE = new int[][]{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
static Queue<List<int[]>> QUEUE;
static List<int[]> NEXT_ITEMS;
static boolean[][] VISITED;
static int ANS;
/**
* 测试入口
*/
public static void main(String[] args) {
initData();
ANS = resolve();
System.out.println(ANS);
}
/**
* 初始化数据
*/
private static void initData() {
MAP = new char[R][C];
VISITED = new boolean[R][C];
QUEUE = new ArrayDeque<>();
NEXT_ITEMS = new ArrayList<>();
ANS = 0;
QUEUE.offer(BODY);
for (int[] cell : BODY) {
// 将指定的点的集合标记为已访问
VISITED[cell[0]][cell[1]] = true;
}
}
/**
* 求解过程(标准BFS过程)
* @return 最小距离(也可以直接用ANS,不用返回值)
*/
private static int resolve() {
while (!QUEUE.isEmpty()) {
ANS++;
while (!QUEUE.isEmpty()) {
List<int[]> body = QUEUE.poll();
for (int[] shift : MOVE) {
boolean[] result = how(body, shift);
if (!result[0]) {
// 当前偏移不可达,继续下一个偏移检查
continue;
}
if (result[1]) {
// 终止条件达成,返回当前距离(最小距离)
return ANS;
}
// 当前偏移可通过,加入下一次偏移的集合
List<int[]> moved = new ArrayList<>();
for (int[] cell : body) {
int nx = cell[0] + shift[0];
int ny = cell[1] + shift[1];
// 添加新的偏移后的点
moved.add(new int[]{nx, ny});
// 设置新的偏移点未已访问
VISITED[nx][ny] = true;
}
NEXT_ITEMS.add(moved);
}
}
QUEUE.addAll(NEXT_ITEMS);
NEXT_ITEMS.clear();
}
return -1;
}
private static boolean[] how(List<int[]> body, int[] shift) {
// 是否可达标记
boolean couldGo = false;
// 是否满足终止条件标记
boolean touch = false;
for (int[] cell : body) {
int nx = cell[0] + shift[0];
int ny = cell[1] + shift[1];
if (nx >= 0 && nx < R && ny >= 0 && ny < C) {
// 偏移的点在MAP范围内,进一步判断
if ('O' == MAP[nx][ny]) {
// 满足终止条件,变更标记
touch = true;
}
if ('W' == MAP[nx][ny]) {
// 偏移后的点不可达,修改可达标记,跳出
// 因为下一个if的判断,此处必须修改可达标记!
couldGo = false;
break;
}
if (!VISITED[nx][ny]) {
// 任意一个偏移后的点未访问,则认为此次偏移后的整体未访问过,修改可达标记
couldGo = true;
}
} else {
// 偏移的点在MAP范围外,该偏移不可达,跳出
couldGo = false;
break;
}
}
return new boolean[]{couldGo, touch};
}
}最后
以上算法就是对此类问题的个人理解,当然这个算法思路在其他类似的模型中也能适用。如果您有更好的解法思路,请留言交流哈~
原文:https://www.jeremysong.cn/cn/move-array/
欢迎关注我的公众号“须弥零一”,更多技术文章第一时间推送。
评论
