复杂度 O、Θ、Ω、o、ω,别再傻傻分不清了!
共 427字,需浏览 1分钟
·
2020-09-28 21:34

Java技术栈
www.javastack.cn
关注阅读更多优质文章
转自公众号:彤哥读源码
前言
在我们表示复杂度的时候,通常使用大O来表示。
但是,在其他书籍中,你可能还见过Θ、Ω、o、ω等符号。
那么,这些符号又是什么意思呢?
本节,我们就来解决这个问题。
读音
我们先来纠正一波读音:
O,/əʊ/,大Oh
o,/əʊ/,小oh
Θ,/ˈθiːtə/,theta
Ω,/oʊˈmeɡə/,大Omega
ω,/oʊˈmeɡə/,小omega
是不是跟老师教得不太一样^^
数学解释
Θ
Θ定义了一种精确的渐近行为(exact asymptotic behavior),怎么说呢?
用函数来表示:
对于f(n),存在正数n0、c1、c2,使得当 n>=n0 时,始终存在 0 <= c1*g(n) <= f(n) <= c2*g(n),则我们可以用 f(n)=Θ(g(n))表示。
用图来表示:
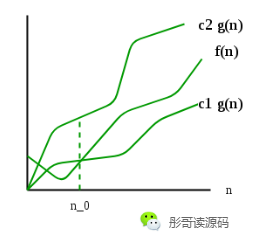
Θ同时定义了上界和下界,f(n)位于上界和下界之间,且包含等号。
比如说,f(n) = 2n^2+3n+1 = Θ(n^2),此时,g(n)就是用f(n)去掉低阶项和常数项得来的,因为肯定存在某个正数n0、c1、c2,使得 0 <= c1*n^2 <= 2n^2+3n+1 <= c2*n^2,当然,你说g(n)是2*n^2也没问题,所以,g(n)实际上满足这个条件的一组函数。
好了,如果Θ你能理解了,下面四个就好理解了。
O
O定义了算法的上界。
用函数来表示:
对于f(n),存在正数n0、c,使得当 n>=n0 时,始终存在 0 <= f(n) <= c*g(n),则我们可以用 f(n)=O(g(n))表示。
用图来表示:
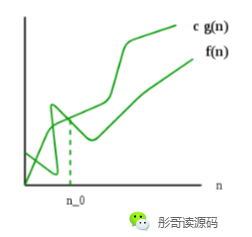
O只定义上界,只要f(n)不大于c*g(n),就可以说 f(n)=O(g(n))。
比如说,对于插入排序,我们说它的时间复杂度是O(n^2),但是,如果用Θ来表示,则必须分成两条:
最坏的情况下,它的时间复杂度为Θ(n^2);
最好的情况下,它的时间复杂度为Θ(n)。
这里的n^2只是g(n)这一组函数中最小的上界,当然,g(n)也可以等于n^3。
不过,我们一般说复杂度都是指的最小的上界,比如,这里插入排序的时间复杂度如果说是O(n^3),从理论上来说,也没问题,只是不符合约定罢了。
插入排序最好的情况就是数组本身就是有序的。
o
o定义的也是算法的上界,不过它不包含等于,是一种不精确的上界,或者称作松上界(某些书籍翻译为非紧上界)。
用函数来表示:
对于f(n),存在正数n0、c,使得当 n>n0 时,始终存在 0 <= f(n) < c*g(n),则我们可以用 f(n)=o(g(n))表示。
用图来表示:

o表示仅仅是大O去掉等于的情况,其他行为与大O一模一样。
Ω
Ω定义了算法的下界,与O正好相反。
用函数来表示:
对于f(n),存在正数n0、c,使得当 n>=n0 时,始终存在 0 <= c*g(n) <= f(n),则我们可以用 f(n)=Ω(g(n))表示。
用图来表示:
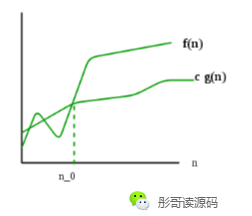
Ω只定义下界,只要f(n)不小于c*g(n),就可以说 f(n)=Ω(g(n))。
比如,对于插入排序,我们可以说它的时间复杂度为Ω(n),不过,这通常没有什么意义,因为插入排序在最好的情况下很少,基本都是在最坏情况或者平均情况。
ω
ω同样定义的是下界,只不过不包含等于,是一种不精确的下界,或者称作松下界(某些书籍翻译为非紧下界)。
用函数来表示:
对于f(n),存在正数n0、c,使得当 n>n0 时,始终存在 0 <= c*g(n) < f(n),则我们可以用 f(n)=ω(g(n))表示。
用图来表示:

ω表示仅仅是大Ω去掉等于的情况,其他行为与大Ω一模一样。
通俗理解
| 符号 | 含义 | 通俗理解 |
|---|---|---|
| Θ | 精确的渐近行为 | 相当于“=” |
| O | 上界 | 相当于“<=” |
| o | 松上界 | 相当于“<” |
| Ω | 下界 | 相当于“>=” |
| ω | 松下界 | 相当于“>” |
小结
为了帮助同学们快速查阅英文资料,彤哥特地把这几节涉及到的英语单词汇总了一下:
| 汉语 | 英文 |
|---|---|
| 复杂度 | complexity |
| 时间复杂度 | time complexity |
| 空间复杂度 | space complexity |
| 渐近分析 | asymptotic analysis |
| 最坏情况 | the worst case |
| 最好情况 | the best case |
| 平均情况 | the average case |
| 精确的渐近行为 | exact asymptotic behavior |
| 低阶项 | low order terms |
| 常数项(前置常数) | leading constants |
| 松上界 | loose upper-bound |
后记






关注Java技术栈看更多干货


