词向量背后精妙的数学
共 3807字，需浏览 8分钟
·
2020-12-04 11:09
来自 | 知乎 作者 | 潘小小
词向量在NLP领域已经是一个通用的预处理方法了。随遇几乎所有处理语言的程序，它们现在的默认输入就已经是词向量了。然而，对于最简单的word2vec，我们似乎仍有一些不了解的地方。
Word2Vec的Skip-gram架构
Word2Vec的核心思想，就是要用一些较短的向量来表示不同的词。而向量与向量之间的关系，则可以表示词与词之间的关系。总结来说，常常使用的有两种关系：
首先是向量之间的夹角，用以表示词与词之间「含义的相似度」。夹角越小，方向就越一致，词的意思也就越相似。另一种关系，则是词语含义的隐藏维度。这里有一个非常著名的例子：
两边各自做减法，得到的差向量居然几乎一样。这种现象的出现，正是因为word2vec的词向量中还隐藏着词语的抽象维度。国王的向量，减去王后的向量，就恰好得到了性别的维度。
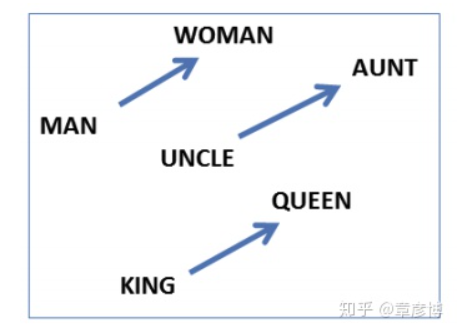
正式这两个重要的性质，赋予了词向量强大的力量。
要实现这一性质，核心在于定义什么叫「相似」。
符号、字形、发音，这些都不重要，最重要的是关系。
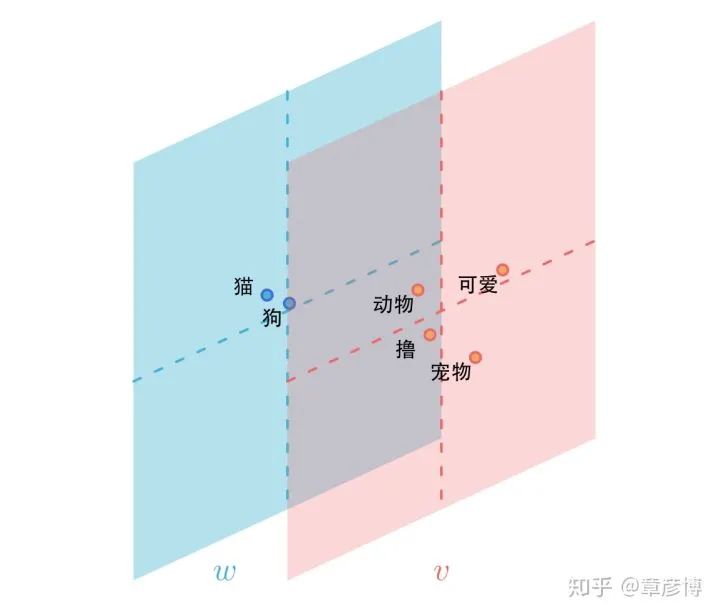
两个词，「猫」、「狗」，它们都和「宠物、撸、可爱、动物……」一起出现，那「猫」和「狗」就很相似。这就是结构主义的思想。
为了方便后面论述，我们称「宠物、撸、可爱、动物」等与「猫」一起出现的词为「猫的上下文」。猫则是「目标词」。
这个时候，如果我们给猫、狗各一个向量，并要求用这个向量预测它们的上下文，就是所谓的skip-gram算法。由于它们的上下文几乎一样，所以作为输入的词向量也会几乎一样。这样，我们就实现了一个重要的目标：上下文相似的几个词语，它们的词向量也相似。
更准确的，对于两个共同出现的词语i与j，我们会要求优化一个loss函数l：
在这个函数中，第一部分就是预测的部分。向量 
与向量 
做内积，内积越大loss就会越小。我们还可以从预测的角度来看这个内积， 
越大，代表模型认为i与j共同出现的概率越大。从而，用这种方法，我们可以用词向量的点积预测它的上下文。
函数的第二部分称为「负采样」，我们从一个分布 
中随机采样出一个词n，然后会希望 
越小越好。
从直觉上看，这个优化过程在做两件事：
让相连的词的词向量
与 靠近；让不相连的词的词向量
与 
远离。
这里有一个至关重要的细节：我们拉近的不是 与 
，而是 与 。这意味着，词向量嵌入并不是简单的把共同出现的词拉近，而是将词与它的上下文拉近。在这里，w是词的嵌入，而v是上下文的嵌入。正是通过这个方法，实现了开头对于「相似」的定义——拥有相似上下文的词，其词向量嵌入也相似。
词向量的两个空间
词向量嵌入的两个空间常常被人忽视。在实际应用中，使用的也通常只是词的嵌入，也就是w。但是，w与v放在一起，才可以得到最完整的信息。在一篇叫做《Improving Document Ranking with Dual Word Embeddings》[1]的小众论文中，作者展示了这样一个有意思的表格：
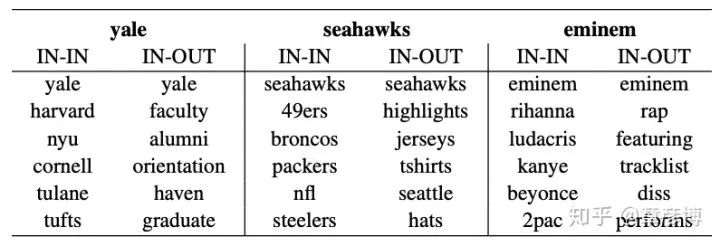
表格中的IN代表词的嵌入，也就是上面说的w；OUT代表上下文的嵌入，也就是前面说的v。举个例子，如果考察Yale（耶鲁）这个词，那么与Yale的词嵌入最近的词嵌入是Harvard, NYU, Cornell这样的大学。它们都有相同的性质，那就是「它们都是大学」。
但如果考察Yale的词嵌入与上下文嵌入的关系，就会出现一个有趣的现象：在上下文的空间中，与Yale的词空间向量嵌入最接近变成了faculty, alumni, orientation这样的词汇。它们都是大学之中的事物。实际上，它们就对应了数据中共同出现的词汇。
作者还实验了使用IN-OUT替代IN-IN做一些工程实验，取得了比之前更好的结果。但这里我们按下不表，相比于工程的成功，这个细节可以引出一个更有意思的观点——Skip-gram的词向量嵌入，实际上是在做（加权的）矩阵分解。
Skip-gram的数学
现在我们知道了词向量嵌入存在两个空间，w与v。对于 与 ，它们点乘总能得到一个标量 
。我们可以反过来看，认为词向量的训练就是在对 
做矩阵分解。
那么，问题就来了，M 矩阵是什么？
要回答这个问题，就要从头对skip-gram的数学做一个推导。2014年的这篇文章[2]给出了详细的推导，这里我简略的叙述一下。
在一开始，我给出了对于共同出现的两个词i与j贡献的loss值：
对于真正的训练，其loss实际上要乘上(i,j)出现的的概率。所以，理论上的loss期望值是：
也就是：
这里用 
代表数据中i,j共同出现的概率，以及出现i的边缘分布。用 
表示负采样的概率分布。通过这种方法，我们就消去了一开始的 
，式子中就只有一个 
了。
令 
，原式变为：
这样，我们就只需要求 
的解，就能得知M的形式了：
可以很容易地解得：
这个形式就很有意思了。我们考虑两种负采样的分布，一种令 
，用数据中的出现频率作为负采样；另一种令 
为一个均匀的负采样，N是词的总量。
带入前者，得到的就是 
，其中PMI就是Pointwise Mutual Information的简称，即「点互信息」，描述的是词i与词j之间的一种相关性，即：知道了词i出现后，对于词j是否出现的不确定度的消减程度。其值越高，意味着i与j的正向关联越大。
而如果带入后者， ，就会得到 
，也就是条件概率的对数。
同时，我们也能看到一个有意思的结果——负采样是必须的，而不是锦上添花的「优化」。不做负采样，就意味着k=0。要使得loss最小，M就必须逼近正无穷大。而只要对每一对数据做一次负采样，就足以消除这种可能性。
词向量究竟在做什么？
有了前面的理论基础，我们终于可以讨论词向量的行为了。词向量在对什么进行建模？两个词的词向量(w)如果相似，到底是什么相似？
答案呼之欲出——词向量在对PMI或者是条件概率进行建模。具体是哪一种，要取决于负采样的方式。词向量通过矩阵分解的方式将PMI（或条件概率）矩阵降维，得到我们所需的向量。
词向量分解相比于SVD的一个好处，在于这里的分解还是加权的！经常出现的词，其重构的误差就越小；而少量出现的词，其误差的容忍度就越大。这是传统SVD难以做到的。
而要讨论「词向量的相似」是什么意思，可以以PMI作为例子，来看一个具体的问题：如果两个词，例如「猫」、「狗」的词向量相似，到底意味着什么相似？我们来看看下面这张图：
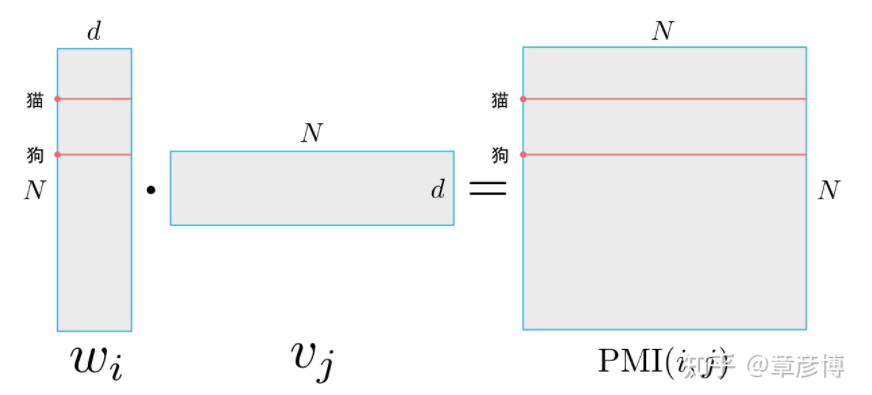
对于一个有N个词、嵌入到d维的词向量训练结果，当猫与狗的词向量几乎一样时，其意味着点乘得到的PMI矩阵的猫、狗行向量几乎一样。
这说明，词向量(w)相似，意味着两个词与其他所有词的PMI都相似。换成另一种负采样，就是两个词的上下文的条件概率相似。
这里有一个非常值得思考的现象：我们直接训练的是w与v，而M作为w与v的函数，是一个非常有意义的量。我们如何将这个过程反转过来——我需要PMI，如何设计一个简洁优雅的训练？而且，直接被训练的还不一定是PMI。
参考
^Nalisnick, E., Mitra, B., Craswell, N., & Caruana, R. (2016, April). Improving document ranking with dual word embeddings. In Proceedings of the 25th International Conference Companion on World Wide Web (pp. 83-84). https://www.microsoft.com/en-us/research/wp-content/uploads/2016/04/pp1291-Nalisnick.pdf ^Levy, O., & Goldberg, Y. (2014). Neural word embedding as implicit matrix factorization. In Advances in neural information processing systems (pp. 2177-2185). http://papers.nips.cc/paper/5477-neural-word-embedding-as-implicit-matrix-factorization.pdf
—完— 推荐阅读： Pandas数据可视化原来也这么厉害 画图神器pyecharts-旭日图 刷爆网络的动态条形图，3行Python代码就能搞定 Python中读取图片的6种方式 2020年11月国内大数据竞赛信息-奖池5000万 Python字典详解-超级完整版 刷爆网络的动态条形图，3行Python代码就能搞定 一个有意思还有用的Python包-汉字转换拼音
学习交流群
↓扫码关注本号↓