一文了解点特征直方图

重磅干货，第一时间送达

3D中特征检测和匹配的目标与2D中大致相同：从不同的角度查找可以与同一场景的扫描进行匹配。这些功能匹配可用于初始化oraidin注册。但是，3D数据的性质要求我们重新考虑什么指数比较适合用来计算。虽然没有具有相关强度的统一像素网格，但是却有了基本相同的非均匀数据点集合。

对于一个特定的点云，法线方向与该表面的曲率概率是基本的几何特征的描述。尽管计算简单，快速，但是在大多数情况下，点云将包含许多相似或相同的特征值，这使得无法获取更多信息和特征。我们着重介绍一些快速和高效的局部和全局3D点云特征检测算法。

平面的法线向量是垂直于平面的单位向量，并且表面上某个点的法线向量定义为垂直于与表面相切的平面的向量。

检测点的法线向量的计算主要包括基于表面网格的求解方法和基于周围邻域中的点的分布的求解方法。

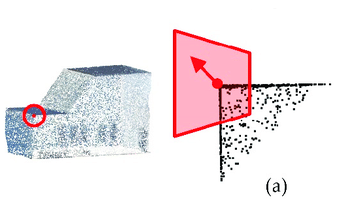
用于正常估计的不同区域选择

法线向量所在的轴是邻域分布的分散方向。假设距N个检测点的距离的半径位于r的附近，则相邻点与查询点p_i之间的协方差矩阵为：

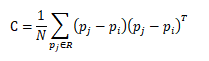
计算C的特征值和特征向量，并按降序{λ1，λ2，λ3}和相应的特征向量{e1，e2，e3}排列特征值。

其中，最大值λ1表示邻域点主要集中在相应的特征向量e1上，最小值λ3表示邻域点e3最分散在相应的特征向量上，因此特征向量e3表示法线向量。

点特征直方图（PFH）通过使用围绕点的多维直方图的平均曲率来编码点的k个最近邻点的几何特性。这个高维空间提供了一些有用的特征表示，而对于6维可以保持不变，并且可以应付相邻的不同采样密度和噪声水平。

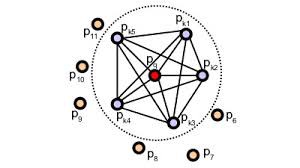
PFH的影响范围

半径为r的球的球心及其所有相邻点相互连接形成网络。最终的PFH几何特征将是通过计算邻域中所有对点之间的变化关系而获得的直方图。

为了计算给定两个点和，pi和pj以及它们相关的法线ns和nj两者之间的相对差，我们在特定点处定义了固定坐标系。

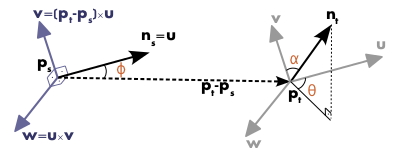
使用上面的uvw坐标系，可以将ns法线和ni法线之间的差分解为以下3个角度差。

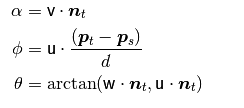
保存这些变量以及点之间的欧几里得距离，然后在计算所有对时将它们合并到直方图中。最终的描述符是每个变量的直方图的串联。

快点特征直方图（FPFH）是PFH的扩展，它具有PFH的这种几何特征，具有其大多数特征和相同的原理。

FPFH的输入也是具有正常信息的点云，输出是可以反映每个点周围邻域特征的直方图。但是与PFH不同，将采取一些简化和优化措施来加快FPFH的计算。

下面专门介绍FPFH如何通过简化和优化来加快计算速度。首先，对于每个点，使用类似于PFH的方法来计算三元组，并获得简化的点特征直方图，称为SPFH。使用加权的邻近SPFH来计算直方图的最终值，如下所示：

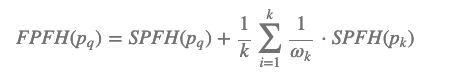
权重取决于给定距离度量空间上的中心点和相邻点。当然，这里也可以使用其他测量方法来设置该重量。