从零实现深度学习框架(十)线性回归简介

引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
我们自动求导工具第一阶段的实现已经完成了,本文最简单的模型——线性回归模型进行简单的介绍。
线性回归
给定输入,可能有多个维度(特征),和输出。线性回归(linear regression)假设输入和输出之间的关系是线性的。即可以表示为中元素的加权和,这里通常允许包含观测值的一些噪声,我们假设任何噪声都比较正常,比如噪声遵循高斯分布。
我们举一个例子:我们希望根据房屋的面积(㎡)和房龄(年)来估计房屋的售价(万/㎡)。以某卖房软件上深圳南山区近地铁口售价的真实数据为例。我们收集了房屋的售价、面积和房龄。在机器学习中,该数据集称为训练集(training data set)。每行数据(一次房屋交易相对应的数据)称为样本(sample),也称为数据点(data point)。我们把试图预测的目标(比如房屋价格)称为标签(label)或目标(target)。预测所依据的自变量(面积或房龄)称为特征(feature)。
我们使用来表示数据集中的样本数,对索引为的样本,其输入表示为,其对应的标签是。
我们收集到的数据集如下:
X = [
[64.4, 31], # [面积, 房龄]
[68, 21],
[74.1, 19],
[74.8, 24],
[76.9, 17],
[78.1, 16],
[78.6, 17]
]
y = [6.1, 6.25, 7.8, 6.66, 7.82, 7.14, 8.02]
线性回归假设目标(房屋价格)可以表示为特征(面积和房龄)的加权和,如下:
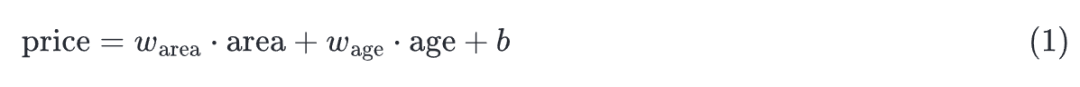
有了数据集以后,我们的目标是寻找线性回归模型的权重和偏置,以对新的样本进行预测。
在机器学习领域,我们使用的一般是高维数据集,建模时采用线性代数表示法会比较方便。假设我们的输入包含个特征时,我们将预测结果表示为:
比如在我们房价预测的例子中总共有2个特征,分别是房屋面积和房龄。所以可以写成:
假设表示面积;表示房龄。
如果将所有的特征都放到向量中,并将所有权重放到向量中,我们可以用点积形式来简介地表达模型:
向量表示包含所有特征的单个样本数据。那么用符号可以表示我们整个数据集中的个样本,其中,的每一行是一个样本,每一列是一种特征。
那么预测值就可以通过矩阵-向量乘法表示:
有时候也可以把加到权重中去,也进行相应的变化得到增广矩阵。上面的式子展开如下:
这里的会进行广播。我们如果把加到权重中去,就变成了:
上式最后用和表示增广后的矩阵和向量。
我们已经有了数据集和模型,那么如何得到模型参数呢?答案就是学习过程。
学习过程
学习过程说的是:基于初始的模型参数,我们可以得到一个预测输出,然后我们计算该输出和真实输出之间的距离。通过最小化损失函数和优化方法就可以来优化模型参数。
损失函数:衡量实际值与预测值之间的差距。数值越小代表损失越小,完美预测时损失为0。
优化:改变模型参数以获得更少的损失
损失函数

我们为一维情况下的回归问题绘制图像,如上图所示。一维情况即样本只有一个特征。比如横坐标代表身高,纵坐标代表体重。
假设某人的真实身高是180cm,你预测的身高是156cm。那么衡量距离,你首先想到的应该是它们之间的差值。为了避免负数,也应该加一个绝对值。所以定义为,但是绝对值是不可求导的,我们可以把绝对值改成平方,并加上系数好进行求导。这就是平方误差损失函数:

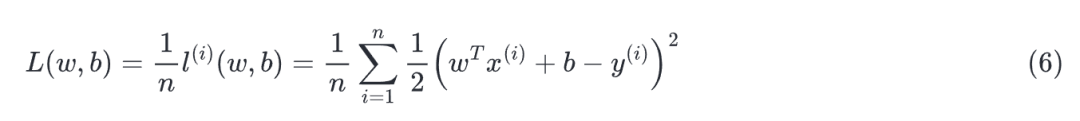
我们要找的就是能使所有训练样本上的损失均值最小的参数:

梯度下降
对于线性回归来说,有一种方法叫作解析解。但是它应用有限,无法进行推广。因此这里不做分析。
本节介绍的方法即使我们无法得到解析解的情况下,仍然可以有效地训练模型。
那就是梯度下降(gradient descent)的方法,这种方法几乎可以优化所有的深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。
梯度下降最简单的用法是计算损失函数关于模型参数的导数(或者说是梯度)。通常是遍历完整个数据集再进行参数更新,但实际上可能非常慢。因此我们遍历的时候只遍历部分批量数据,遍历完该批量数据即进行参数更新。
我们刚刚看到的方法叫作小批量随机梯度下降法,随机指的是每批数据都是随机抽取的。
用下面的数学公式来表示这一更新过程:
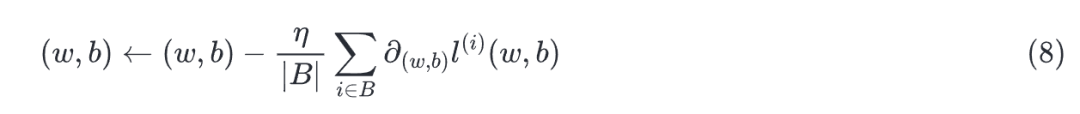
其中表示偏导数;代表小批量数据;表示这一小批量数据的数量;是学习率。
算法的步骤如下:
初始化模型参数,通常采用随机初始化 从数据集中随机抽取小批量样本,且在梯度的反方向上更新参数,不断迭代这一步骤。
批量大小和学习率的值通常需要预先指定,而不是通过学习得到的,这种参数叫作超参数(hyperparameter)。
在训练了预先确定的若干次迭代次数后(或满足某些停止条件),我们保存此时模型参数的估计值,记为。
优化方法
线性回归恰好只有一个最小值,但是对于深度神经网络这种复杂的模型来说,可能有多个局部极小值点。
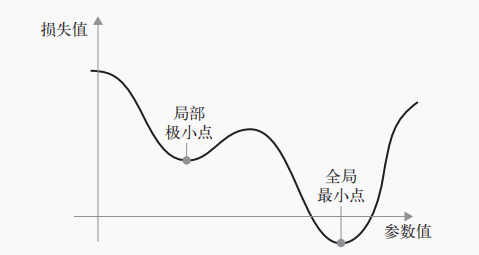
此时可能需要用到随机梯度下降法的一些变体,比如Adagrad、RMSProp等。这些变体被称为优化方法或优化器。
关于这些变体后面的文章会讨论。
从最大似然来看均方误差
本节来看一下为什么采用均分误差作为损失函数。
我们上面说过,假设噪声(误差)遵循高斯分布(正态分布)。为什么要这么假设呢,一种解释是,根据中心极限定理:许多独立随机变量的和趋向于正态分布。因为影响噪声的因素有很多,而这些因素都是独立且随机分布的,所以这么假设。
若随机变量具有均值和方差,其正态分布概率密度函数如下:
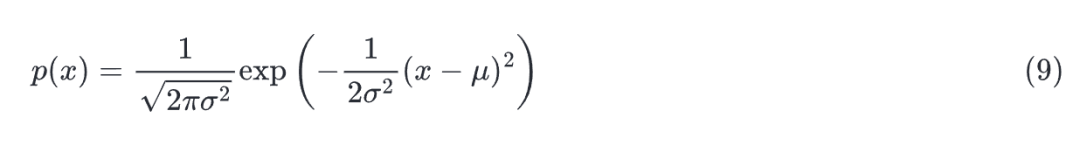

改变均值会产生沿轴的偏移,增加方差会降低分布的峰值。
均方误差损失函数(简称均方误差)可以用于线性回归的一个原因是:我们假设了观测中包含噪声,其中噪声服从正态分布。则预测函数可以写为:
其中,有
根据,也可写成。
因此,我们可以写出给定观测到特定的似然:
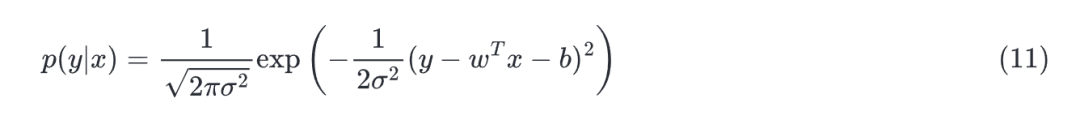
参数和的最优值是使整个数据集的似然最大的值:

由于取对数不改变单调性,同时优化一般是指最小化,我们再加上负号,变成最小化负对数似然,由此可得:

代入得:
上面式子的解并不依赖于,因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。
参考
动手学习深度学习
最后一句:BUG,走你!


Markdown笔记神器Typora配置Gitee图床
不会真有人觉得聊天机器人难吧(一)
Spring Cloud学习笔记(一)
没有人比我更懂Spring Boot(一)
入门人工智能必备的线性代数基础
1.看到这里了就点个在看支持下吧,你的在看是我创作的动力。
2.关注公众号,每天为您分享原创或精选文章!
3.特殊阶段,带好口罩,做好个人防护。
