「@Author：Runsen」

插入排序

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。

一个有序的数组，我们往里面添加一个新的数据后，如何继续保持数据有序呢？很简单，我们只要遍历数组，找到数据应该插入的位置将其插入即可。

通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

因此，代码编写需要判断插入元素和当前元素的大小关系，遍历时需要从数组的第二个数开始。

如果插入元素大于当前元素，则将待插入元素插入到当前元素的后一位。

如果插入元素小于当前元素，则将当前元素后移一位。直到找到一个当前元素小于插入元素。

因此，在for循环遍历时，又有一个while内循环的条件，条件的内容是插入元素的索引减一和零进行对比。如果插入元素小于当前元素，同时对索引进行减一操作。如果出现了索引等于零的情况，那么表示插入元素等于当前元素。

下面是插入排序的具体Python代码。

def insert_sort(a):
    length = len(a)
    if length <= 1:
        return a
    # 从数组的第二个数开始
    for i in range(1, length):
        # 从后向前扫描
        j = i - 1
        # value指的是插入元素
        value = a[i]
        while j >= 0:
            if a[j] < value:
                # 插入元素大于当前元素，则将待插入元素插入到当前元素的后一位
                a[j + 1] = value
                break
            else:
                # 插入元素小于当前元素，则将当前元素后移一位
                a[j + 1] = a[j]
                if j == 0:
                    a[j] = value
            j -= 1
    return a


def insertionSort(arr):
    # 对上面的代码进行简单化
    for i in range(len(arr)):
        preIndex = i - 1
        current = arr[i]
        while preIndex >= 0 and arr[preIndex] > current:
            arr[preIndex + 1] = arr[preIndex]
            preIndex -= 1
        arr[preIndex + 1] = current
    return arr

if __name__ == '__main__':
    nums = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    insert_sort(nums)
    print(nums) # [17, 20, 26, 31, 44, 54, 55, 77, 93]

下面对Python代码改为Java代码。代码来自菜鸟教程。

// Java
import java.util.Arrays;

public class Solution {
    public static void main(String[] args) {
        InsertSort(new int[] { 9 ,20 , 10, 13 , 12});
    }
    public static void InsertSort(int [] arr){
        int value; //待插入元素
        int index; //初始值为待插入元素前一个元素的索引

        for(int i= 1 ; i< arr.length;i++){
            //i从第二个元素开始，默认第一个元素是有序的
            //循环条件是小于数组长度，因为也要将最后一个元素插入到前面的序列
            value = arr[i];
            index = i - 1;//初始为前一个元素
            while(index >=0 && value < arr[index]){
                //需要保证index合法
                //每当前面的元素比待插入元素大，就向后移动
                arr[index + 1] = arr[index];
                //不用怕覆盖，因为value保存着待插入的值
                index--;
            }
            //当退出循环，表明已经找到了待插入位置，即index + 1
            arr[index + 1] = value;
        }

        System.out.println(Arrays.toString(arr));
    }
}

下面对Python代码改为JavaScript代码。代码来自菜鸟教程。

// JavaScript
function insertionSort(arr) {
    var len = arr.length;
    // JavaScript需要声明变量先
    var preIndex, current;
    for (var i = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while(preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex+1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex+1] = current;
    }
    return arr;
}

对于不同的查找插入点方法（从头到尾、从尾到头），元素的比较次数是有区别的。但对于一个给定的初始序列，移动操作的次数总是固定的，就等于逆序度。

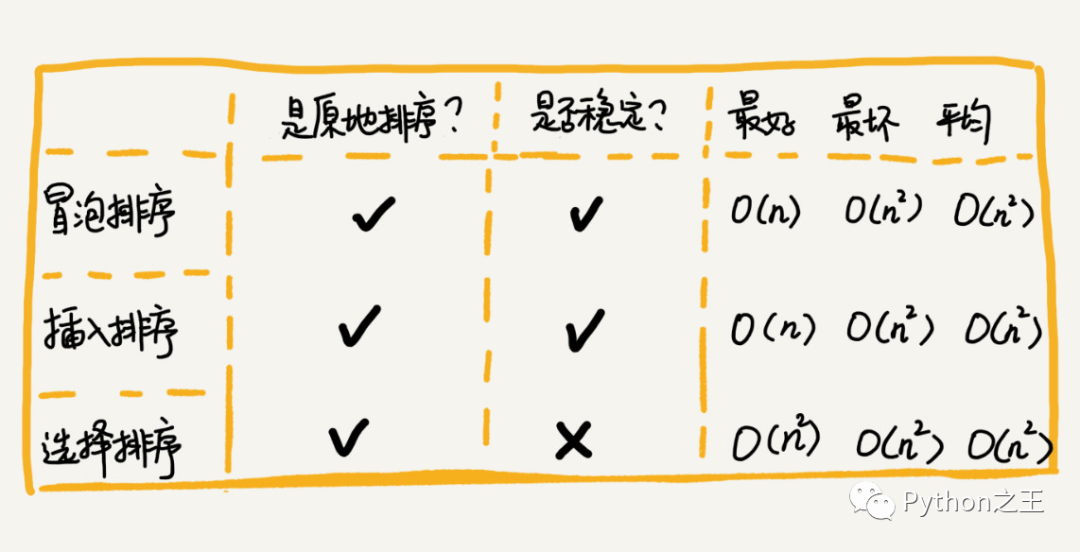
在插入排序中，对于值相同的元素，我们可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行 n 次插入操作，所以平均时间复杂度为 O(n2)。

如果输入数组已经是排好序的话，插入排序出现最佳情况，其运行时间是输入规模的一个线性函数，其时间代价是O(n)。

如果输入数组是逆序排列的，将出现最坏情况。平均情况与最坏情况一样，其时间代价是 O(n2)。

参考：https://www.runoob.com/w3cnote/insertion-sort.html

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序：首先搜索整个列表，找到最小项的位置，如果该位置不是列表的第1项，就交换这两个位置的元素。然后从列表的第2个元素开始，重复上述过程，直到算法达到整个过程的最后一个位置，图形解释如下

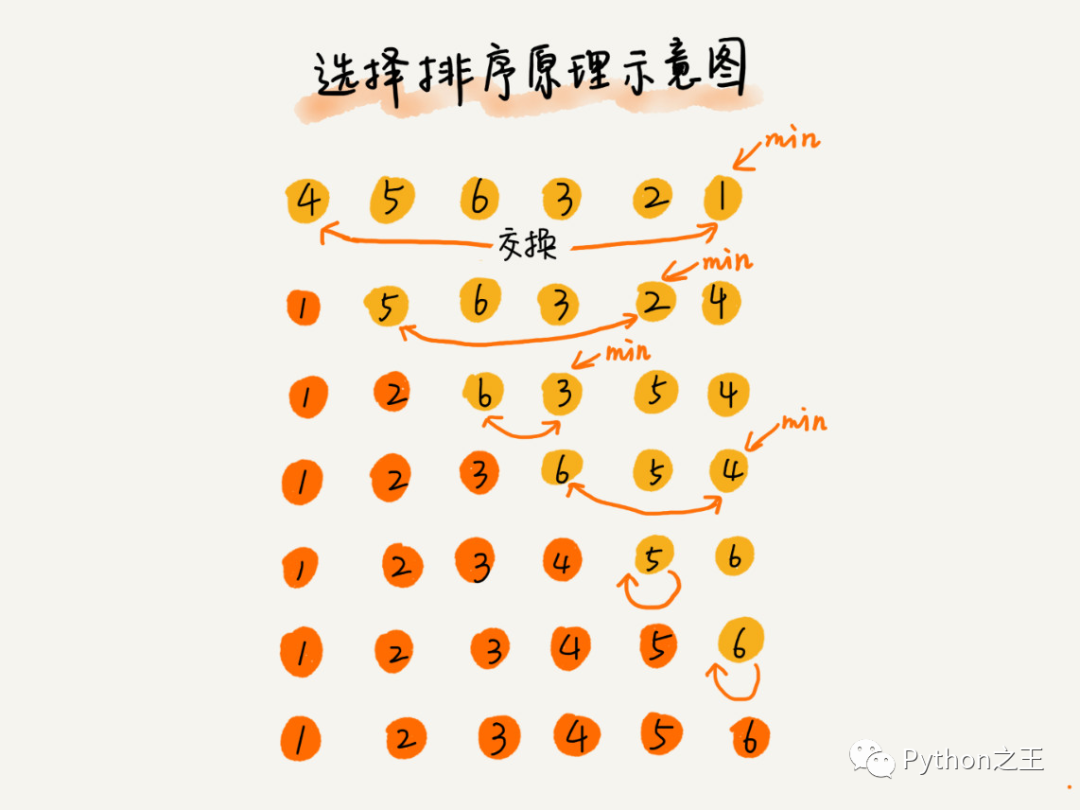
选择排序还有一种代码的形式是将最大值逐一选择到后面，因此遍历的时候需要逆序遍历。

def selection_sort1(nums):
    # 思路是将最小值逐一选择到前面
    n = len(nums)
    # 第一层for表示循环选择的遍数

    for i in range(n - 1):
        min_index = i  # 记录最小值的位置
        # 第二层for表示最小元素和后面的元素逐个比较

        for j in range(i + 1, n):
            if nums[j] < nums[min_index]:
                min_index = j
        if min_index != i:
           # 查找一遍后将最小元素与起始元素互换
            nums[i], nums[min_index] = nums[min_index], nums[i]

def selection_sort2(nums):
    # 思路是将最大值逐一选择到后面
    n = len(nums)
    for i in range(n - 1, 0, -1):
        max_index = i  # 记录最大值的位置
        for j in range(i):
            if nums[j] > nums[max_index]:
                max_index = j
        if max_index != i:
            nums[i], nums[max_index] = nums[max_index], nums[i]

下面对Python代码改为Java代码。代码来自菜鸟教程，选择第一种思路。

下面对Python代码改为JavaScript代码。代码来自菜鸟教程。

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

选择排序是一种不稳定的排序算法。选择排序每次都要找剩余未排序元素中的最小值，并和前面的元素交换位置，这样破坏了稳定性。

当出现几个值相同的时候，比如 5，8，5，2，9这样一组数据，使用选择排序算法来排序的话，第一次找到最小元素 2，与第一个 5 交换位置，那第一个 5 和中间的 5 顺序就变了，所以就不稳定了。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素。

它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换。

无论数列初始状态怎样，在第 i 趟排序中选出最小关键字的记录，需做n-i次比较，因此，总的比较次数为：n(n-1)/2=O(n2)。

因此直接选择排序的平均时间复杂度为 O(n2)。直接选择排序是一个就地排序，空间复杂度为S(n)=O(1)。

参考：https://www.runoob.com/w3cnote/selection-sort.html

参考：极客时间王争算法专栏

❝

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

❞

Reference