浅谈勒让德三平方和定理、拉格朗日四平方和定理
这里介绍下数论中的勒让德三平方和定理、拉格朗日四平方和定理。并介绍如何巧妙利用它进行解决问题

基本原理
「1. 拉格朗日四平方和定理」
拉格朗日四平方和定理,也被称为Bachet猜想。该定理指出任一自然数都可以表示为四个整数平方之和。该定理由拉格朗日于1770年证明。即:
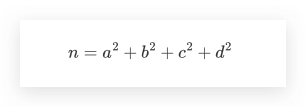
举个栗子,如下所示

「2. 勒让德三平方和定理」
勒让德三平方和定理指出如果一个自然数n符合下述条件时,则可以表示为三个整数平方之和。其中a、b均为非负整数

实践
学习过程中要善于理论联系实际。故在介绍完勒让德三平方和定理、拉格朗日四平方和定理后,现在我们来进行实践。这里以LeetCode的第279题——完全平方数 为例
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是
示例 1
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2
输入:n = 13
输出:2
解释:13 = 4 + 9
提示 1 <= n <= 104
首先说明该题可通过动态规划解决,但这里为了说明上述两个定理的应用。故我们采用数学解法。具体地:
当n满足4^k*(8m+7)形式时,由于不满足勒让德三平方和定理。同时结合拉格朗日四平方和定理易知,此时直接返回4即可 当n不满足4^k*(8m+7)形式时,即满足勒让德三平方和定理。则此时答案只能会是1、2、3中的一个 如果n为一个完全平方数,则此时答案必然为1 如果n满足a^2+b^2形式,即答案为2。则我们只需对所有的a进行枚举,其中a的范围为[1, √n]。然后判断n-a^2是否为完全平方数即可 如果排除了上述所有情形,则答案只能为3。即n满足a^2+b^2+c^2形式
此时,我们不难通过Java实现上述思路。代码如下所示
class Solution {
public int numSquares(int n) {
// 如果不满足 勒让德三平方和定理, 则其必然只能满足 拉格朗日四平方和定理
// 即: n = a*a + b*b + c*c + d*d
if( checkAnswer4(n) ) {
return 4;
}
// 判断是否为 n = a*a 场景
if( isSquare(n) ) {
return 1;
}
// 判断是否为 n = a*a + b*b 场景
for (int a=1; a*a<=n; a++) {
int b = n - a*a;
if( isSquare(b) ) {
return 2;
}
}
// 由于满足勒让德三平方和定理条件, 故此时只可能为3
// 即: n = a*a + b*b + c*c
return 3;
}
/**
* 判断n是否能表示为 4^k*(8m+7) 形式, 即不满足 勒让德三平方和定理
* @param n
* @return
*/
private boolean checkAnswer4(int n) {
while ( n%4==0 ) {
n = n / 4;
}
boolean res = (n%8 == 7);
return res;
}
/**
* 判断是否为完全平方数
* @param n
* @return
*/
private boolean isSquare(int n) {
int x = (int)Math.sqrt(n);
boolean res = ( x*x == n);
return res;
}
}
评论
