从零实现深度学习框架(八)实现常见运算的计算图(上)

引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
在上篇文章中,我们实现了反向传播的模式代码。同时正确地实现了加法运算和乘法运算。从今天开始,我们就来实现剩下的运算。本文实现了减法、除法、矩阵乘法和求和等运算。
实现减法运算
我们先编写测试用例,再实现减法计算图。
test_tensor_sub.py:
import numpy as np
from core.tensor import Tensor
def test_simple_sub():
x = Tensor(1, requires_grad=True)
y = Tensor(2, requires_grad=True)
z = x - y
z.backward()
assert x.grad.data == 1.0
assert y.grad.data == -1.0
def test_array_sub():
x = Tensor([1, 2, 3], requires_grad=True)
y = Tensor([4, 5, 6], requires_grad=True)
z = x - y
assert z.data.tolist() == [-3., -3., -3.]
z.backward(Tensor([1, 1, 1]))
assert x.grad.data.tolist() == [1, 1, 1]
assert y.grad.data.tolist() == [-1, -1, -1]
x -= 0.1
assert x.grad is None
np.testing.assert_array_almost_equal(x.data, [0.9, 1.9, 2.9])
def test_broadcast_sub():
x = Tensor([[1, 2, 3], [4, 5, 6]], requires_grad=True) # (2, 3)
y = Tensor([7, 8, 9], requires_grad=True) # (3, )
z = x - y # shape (2, 3)
assert z.data.tolist() == [[-6, -6, -6], [-3, -3, -3]]
z.backward(Tensor(np.ones_like(x.data)))
assert x.grad.data.tolist() == [[1, 1, 1], [1, 1, 1]]
assert y.grad.data.tolist() == [-2, -2, -2]
然后实现减法的计算图。

class Sub(_Function):
def forward(ctx, x: np.ndarray, y: np.ndarray) -> np.ndarray:
'''
实现 z = x - y
'''
ctx.save_for_backward(x.shape, y.shape)
return x - y
def backward(ctx, grad: Any) -> Any:
shape_x, shape_y = ctx.saved_tensors
return unbroadcast(grad, shape_x), unbroadcast(-grad, shape_y)
这些类都添加到ops.py中。然后跑一下测试用例,结果为:
============================= test session starts ==============================
collecting ... collected 3 items
test_sub.py::test_simple_sub PASSED [ 33%]'numpy.ndarray'>
test_sub.py::test_array_sub PASSED [ 66%]'numpy.ndarray'>
test_sub.py::test_broadcast_sub PASSED [100%]'numpy.ndarray'>
============================== 3 passed in 0.36s ===============================
实现除法运算
编写测试用例:
import numpy as np
from core.tensor import Tensor
def test_simple_div():
'''
测试简单的除法
'''
x = Tensor(1, requires_grad=True)
y = Tensor(2, requires_grad=True)
z = x / y
z.backward()
assert x.grad.data == 0.5
assert y.grad.data == -0.25
def test_array_div():
x = Tensor([1, 2, 3], requires_grad=True)
y = Tensor([2, 4, 6], requires_grad=True)
z = x / y
assert z.data.tolist() == [0.5, 0.5, 0.5]
assert x.data.tolist() == [1, 2, 3]
z.backward(Tensor([1, 1, 1]))
np.testing.assert_array_almost_equal(x.grad.data, [0.5, 0.25, 1 / 6])
np.testing.assert_array_almost_equal(y.grad.data, [-0.25, -1 / 8, -1 / 12])
x /= 0.1
assert x.grad is None
assert x.data.tolist() == [10, 20, 30]
def test_broadcast_div():
x = Tensor([[1, 1, 1], [2, 2, 2]], requires_grad=True) # (2, 3)
y = Tensor([4, 4, 4], requires_grad=True) # (3, )
z = x / y # (2,3) * (3,) => (2,3) * (2,3) -> (2,3)
assert z.data.tolist() == [[0.25, 0.25, 0.25], [0.5, 0.5, 0.5]]
z.backward(Tensor([[1, 1, 1, ], [1, 1, 1]]))
assert x.grad.data.tolist() == [[1/4, 1/4, 1/4], [1/4, 1/4, 1/4]]
assert y.grad.data.tolist() == [-3/16, -3/16, -3/16]
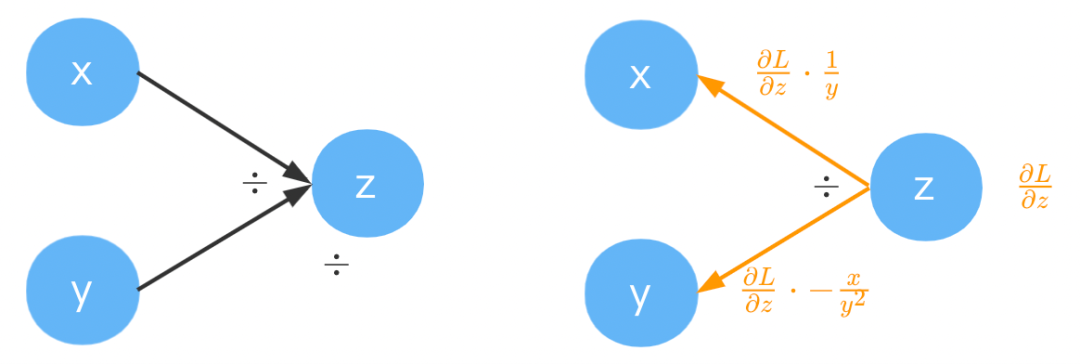
# Python3 只有 __truediv__ 相关魔法方法
class TrueDiv(_Function):
def forward(ctx, x: ndarray, y: ndarray) -> ndarray:
'''
实现 z = x / y
'''
ctx.save_for_backward(x, y)
return x / y
def backward(ctx, grad: ndarray) -> Tuple[ndarray, ndarray]:
x, y = ctx.saved_tensors
return unbroadcast(grad / y, x.shape), unbroadcast(grad * (-x / y ** 2), y.shape)
由于Python3只有 __truediv__ 相关魔法方法,因为为了简单,也将我们的除法命名为TrueDiv。
同时修改tensor中的register方法。
至此,加减乘除都实现好了。下面我们来实现矩阵乘法。
实现矩阵乘法
先写测试用例:
import numpy as np
import torch
from core.tensor import Tensor
from torch import tensor
def test_simple_matmul():
x = Tensor([[1, 2], [3, 4], [5, 6]], requires_grad=True) # (3,2)
y = Tensor([[2], [3]], requires_grad=True) # (2, 1)
z = x @ y # (3,2) @ (2, 1) -> (3,1)
assert z.data.tolist() == [[8], [18], [28]]
grad = Tensor(np.ones_like(z.data))
z.backward(grad)
np.testing.assert_array_equal(x.grad.data, grad.data @ y.data.T)
np.testing.assert_array_equal(y.grad.data, x.data.T @ grad.data)
def test_broadcast_matmul():
x = Tensor(np.arange(2 * 2 * 4).reshape((2, 2, 4)), requires_grad=True) # (2, 2, 4)
y = Tensor(np.arange(2 * 4).reshape((4, 2)), requires_grad=True) # (4, 2)
z = x @ y # (2,2,4) @ (4,2) -> (2,2,4) @ (1,4,2) => (2,2,4) @ (2,4,2) -> (2,2,2)
assert z.shape == (2, 2, 2)
# 引入torch.tensor进行测试
tx = tensor(x.data, dtype=torch.float, requires_grad=True)
ty = tensor(y.data, dtype=torch.float, requires_grad=True)
tz = tx @ ty
assert z.data.tolist() == tz.data.tolist()
grad = np.ones_like(z.data)
z.backward(Tensor(grad))
tz.backward(tensor(grad))
# 和老大哥 pytorch保持一致就行了
assert np.allclose(x.grad.data, tx.grad.numpy())
assert np.allclose(y.grad.data, ty.grad.numpy())
这里矩阵乘法有点复杂,不过都在理解广播和常见的乘法中分析过了。同时我们引入了torch仅用作测试。
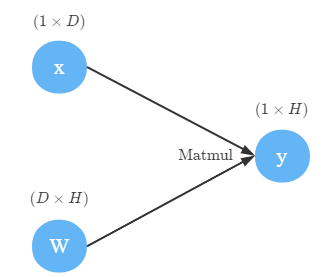
在常见运算的计算图中对句子乘法的反向传播进行了分析。我们下面就来实现:
class Matmul(_Function):
def forward(ctx, x: ndarray, y: ndarray) -> ndarray:
'''
z = x @ y
'''
assert x.ndim > 1 and y.ndim > 1, f"the dim number of x or y must >=2, actual x:{x.ndim} and y:{y.ndim}"
ctx.save_for_backward(x, y)
return x @ y
def backward(ctx, grad: ndarray) -> Tuple[ndarray, ndarray]:
x, y = ctx.saved_tensors
return unbroadcast(grad @ y.swapaxes(-2, -1), x.shape), unbroadcast(x.swapaxes(-2, -1) @ grad, y.shape)
为了适应 (2,2,4) @ (4,2) -> (2,2,4) @ (1,4,2) => (2,2,4) @ (2,4,2) -> (2,2,2)的情况,通过swapaxes交换最后两个维度的轴,而不是简单的转置T。
下面来实现聚合运算,像Sum和Max这些。
实现求和运算
先看测试用例:
import numpy as np
from core.tensor import Tensor
def test_simple_sum():
x = Tensor([1, 2, 3], requires_grad=True)
y = x.sum()
assert y.data == 6
y.backward()
assert x.grad.data.tolist() == [1, 1, 1]
def test_sum_with_grad():
x = Tensor([1, 2, 3], requires_grad=True)
y = x.sum()
y.backward(Tensor(3))
assert x.grad.data.tolist() == [3, 3, 3]
def test_matrix_sum():
x = Tensor([[1, 2, 3], [4, 5, 6]], requires_grad=True) # (2,3)
y = x.sum()
assert y.data == 21
y.backward()
assert x.grad.data.tolist() == np.ones_like(x.data).tolist()
def test_matrix_with_axis():
x = Tensor([[1, 2, 3], [4, 5, 6]], requires_grad=True) # (2,3)
y = x.sum(axis=0) # keepdims = False
assert y.shape == (3,)
assert y.data.tolist() == [5, 7, 9]
y.backward([1, 1, 1])
assert x.grad.data.tolist() == [[1, 1, 1], [1, 1, 1]]
def test_matrix_with_keepdims():
x = Tensor([[1, 2, 3], [4, 5, 6]], requires_grad=True) # (2,3)
y = x.sum(axis=0, keepdims=True) # keepdims = True
assert y.shape == (1, 3)
assert y.data.tolist() == [[5, 7, 9]]
y.backward([1, 1, 1])
assert x.grad.data.tolist() == [[1, 1, 1], [1, 1, 1]]
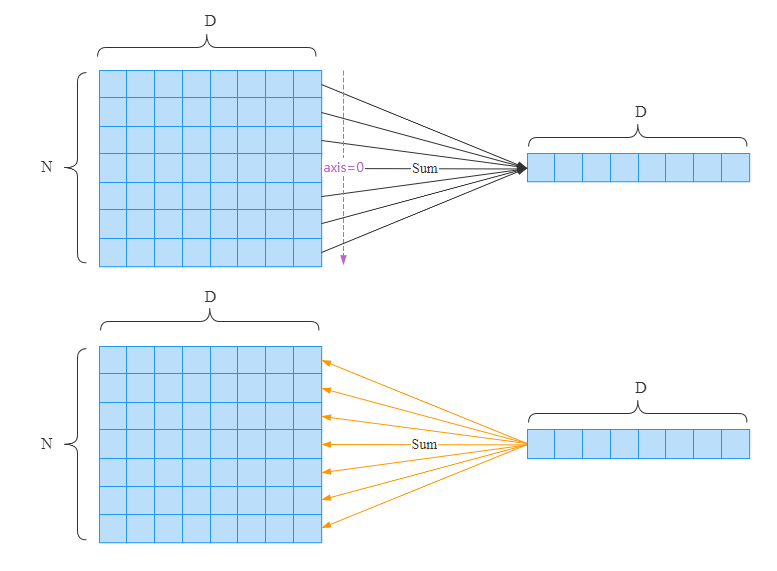
class Sum(_Function):
def forward(ctx, x: ndarray, axis=None, keepdims=False) -> ndarray:
ctx.save_for_backward(x.shape)
return x.sum(axis, keepdims=keepdims)
def backward(ctx, grad: ndarray) -> ndarray:
x_shape, = ctx.saved_tensors
# 将梯度广播成input_shape形状,梯度的维度要和输入的维度一致
return np.broadcast_to(grad, x_shape)
我们这里支持keepdims参数。
下面实现一元操作,比较简单,根据计算图可以直接写出来。
实现Log运算
测试用例:
import math
import numpy as np
from core.tensor import Tensor
def test_simple_log():
x = Tensor(10, requires_grad=True)
z = x.log()
np.testing.assert_array_almost_equal(z.data, math.log(10))
z.backward()
np.testing.assert_array_almost_equal(x.grad.data.tolist(), 0.1)
def test_array_log():
x = Tensor([1, 2, 3], requires_grad=True)
z = x.log()
np.testing.assert_array_almost_equal(z.data, np.log([1, 2, 3]))
z.backward([1, 1, 1])
np.testing.assert_array_almost_equal(x.grad.data.tolist(), [1, 0.5, 1 / 3])

class Log(_Function):
def forward(ctx, x: ndarray) -> ndarray:
ctx.save_for_backward(x)
# log = ln
return np.log(x)
def backward(ctx, grad: ndarray) -> ndarray:
x, = ctx.saved_tensors
return grad / x
实现Exp运算
测试用例:
import numpy as np
from core.tensor import Tensor
def test_simple_exp():
x = Tensor(2, requires_grad=True)
z = x.exp() # e^2
np.testing.assert_array_almost_equal(z.data, np.exp(2))
z.backward()
np.testing.assert_array_almost_equal(x.grad.data, np.exp(2))
def test_array_exp():
x = Tensor([1, 2, 3], requires_grad=True)
z = x.exp()
np.testing.assert_array_almost_equal(z.data, np.exp([1, 2, 3]))
z.backward([1, 1, 1])
np.testing.assert_array_almost_equal(x.grad.data, np.exp([1, 2, 3]))

class Exp(_Function):
def forward(ctx, x: ndarray) -> ndarray:
ctx.save_for_backward(x)
return np.exp(x)
def backward(ctx, grad: ndarray) -> ndarray:
x, = ctx.saved_tensors
return np.exp(x)
实现Pow运算
from core.tensor import Tensor
def test_simple_pow():
x = Tensor(2, requires_grad=True)
y = 2
z = x ** y
assert z.data == 4
z.backward()
assert x.grad.data == 4
def test_array_pow():
x = Tensor([1, 2, 3], requires_grad=True)
y = 3
z = x ** y
assert z.data.tolist() == [1, 8, 27]
z.backward([1, 1, 1])
assert x.grad.data.tolist() == [3, 12, 27]

class Pow(_Function):
def forward(ctx, x: ndarray, c: ndarray) -> ndarray:
ctx.save_for_backward(x, c)
return x ** c
def backward(ctx, grad: ndarray) -> Tuple[ndarray, None]:
x, c = ctx.saved_tensors
# 把c当成一个常量,不需要计算梯度
return grad * c * x ** (c - 1), None
实现,这里看成是常量,变量是。常量不需要计算梯度,我们返回None即可。
实现取负数
其实就是加一个负号y = -x。
import numpy as np
from core.tensor import Tensor
def test_simple_exp():
x = Tensor(2, requires_grad=True)
z = -x # -2
assert z.data == -2
z.backward()
assert x.grad.data == -1
def test_array_exp():
x = Tensor([1, 2, 3], requires_grad=True)
z = -x
np.testing.assert_array_equal(z.data, [-1, -2, -3])
z.backward([1, 1, 1])
np.testing.assert_array_equal(x.grad.data, [-1, -1, -1])

class Neg(_Function):
def forward(ctx, x: ndarray) -> ndarray:
return -x
def backward(ctx, grad: ndarray) -> ndarray:
return -grad
总结
本文实现了常见运算的计算图,下篇文章会实现剩下的诸如求最大值、切片、变形和转置等运算。
最后一句:BUG,走你!


Markdown笔记神器Typora配置Gitee图床
不会真有人觉得聊天机器人难吧(一)
Spring Cloud学习笔记(一)
没有人比我更懂Spring Boot(一)
入门人工智能必备的线性代数基础
1.看到这里了就点个在看支持下吧,你的在看是我创作的动力。
2.关注公众号,每天为您分享原创或精选文章!
3.特殊阶段,带好口罩,做好个人防护。
