原创 | 《相机标定》深入理解原理与实战（一）-轻识

第一章引言

1.1 为什么要相机标定

首先来看相机标定的意义，我们都知道，我们拍摄的图片是二维的，但是真实世界是三维的。一个场景是如何从三维变成二维的呢？相机起到的就是这个作用。我们可以把相机看成一个函数，输入是一个三维的场景，输出是我们获得的二维的图片，这里可以认为是灰度图。我们平时看到的 RGB 彩色图是通过 RGB 三通道来实现的，每个通道可以认为是一张灰度图。从三维世界到二维世界的这个映射关系是不可逆的，也就是说无法仅通过一张二维图来得到真实的三维世界。

相机标定就是通过输入带有标定 pattern 的标定板来计算相机参数，来用简单的数学模型来表达复杂的成像过程。求解这个数学模型，也就是求解相机的参数，包括相机的内参，外参以及畸变参数。有了这个数学模型，我们可以对相机拍摄的图片进行畸变校正，也可以用多个相机拍摄图片来进行三维重建，以及其他的计算机视觉的应用。

图 1.1: 相机标定模型

1.2 成像系统

接下来介绍成像系统的基础，从三维坐标中的某一点 P(x, y, z) 出发，推导在相机的像素坐标系中的成像点。

1.2.1 投影矩阵和小孔成像

首先介绍一下下面会用到的几个专有名词：

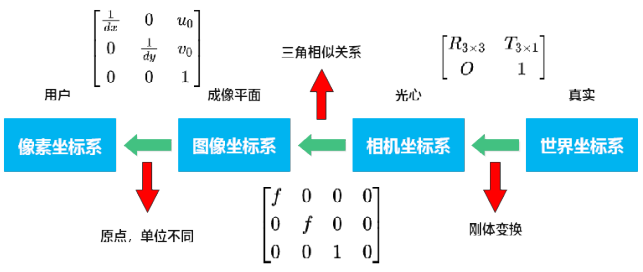
世界坐标系（world Coords）：点在真实世界中的位置，描述相机位置，单位 m。
相机坐标系（Cameras Coords）：以相机 sensor 中心为原点，建立相机坐标系，单位 m。
图像物理坐标系（Film Coords）：经过小孔成像后得到的二维坐标系，单位 mm。
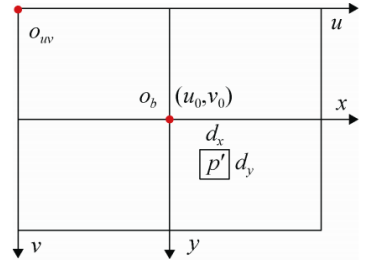
像素坐标系（Pixel Coords）：成像点在相机 sensor 上像素的行数和列数，原点为图像左上角，不带有任何物理单位，或者说单位是 pixel主点：光轴与图像平面的交点为主点，即图1.2中的点 p。
主点：光轴与图像平面的交点为主点，即图1.2中的点 p。

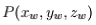接下来我们建立从真实世界（世界坐标系）中的一点到像素坐标系上对应点的映射，这会涉及四个坐标系之间的三步转换。

首先，考虑世界坐标系中的一点

到相机坐标系

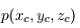的对应关系，他们的转换关系可以通过矩阵 R, T 来表征。R 是相机坐标系相对于世界坐标系的旋转矩阵，T 是相机坐标系相对于世界坐标系的平移矩阵，即相机的中心在世界坐标系的坐标。他们的之间的转换关系可以通过矩阵表示为下面的公式：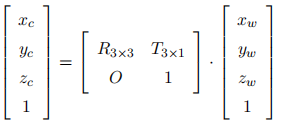

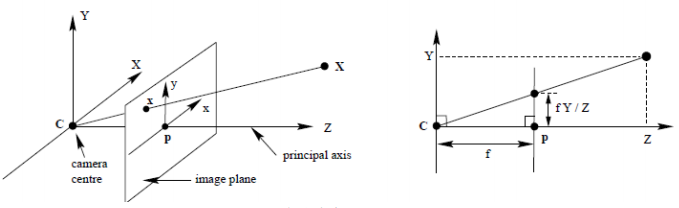
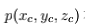图 1.2: 小孔成像原理图

然后，考虑相机坐标系到图像坐标系的转换，假设点

在图像坐标系中的成像点是 p′(x, y)。这里基于的是小孔成像的原理，原理如图1.2的左图所示，焦距是 f，成像面是与 XOY 平面平行且距离原点 f 的平面。图1.2的右图为 ZcY 截面。利用相似三角形可以求出：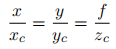

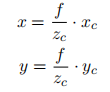
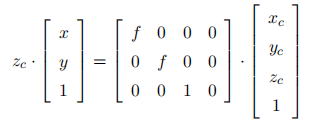
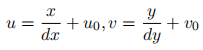
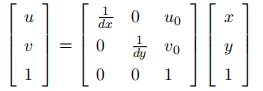
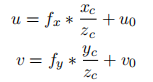
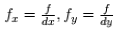化简可以推出：

写成矩阵的形式：

这样便得到了相机坐标系到图像坐标系的转换关系。

图 1.3: 图像坐标系与像素坐标系的转换关系

最后，考虑图像坐标系中点 p′(x, y) 到像素坐标系对应点 (u, v) 的转换关系，如图1.3所示。图像坐标系的原点在 sensor 的中央，像素坐标系的原点在 sensor 的左上角。图像坐标系的单位是 mm，像素坐标系的单位是 pixel。他们的之间的转换关系可以表示为：

转换成矩阵表示：

(u, v) 即点在像素坐标系中的坐标，即像素的列数、行数。dx, dy 为每个像素点在图像坐标系 x 轴，y 轴上的尺寸，单位是毫米/每像素，是每个 sensor 的固有参数。实际情况下，芯片的中心并不在光轴上，安装的时候总会有有些误差，所以引入两个新的参数 (u0, v0)，代表主点在像素坐标系下的偏移。

不考虑世界坐标系的旋转，点从相机坐标系到像素坐标系的转换公式可以总结为

上式中

，代表焦距除以单个的像素大小，所以单位是像素，在相机的标定过程中 dx, dy, f 均不能直接测量得到的，组合值 fx, fy 可以标定得到。zc 是三维点在相机坐标系中深度值。从世界坐标系到像素坐标系，写成矩阵形式，可以得到：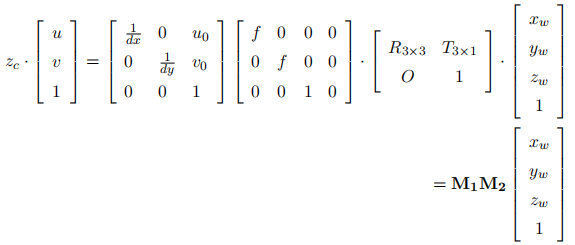

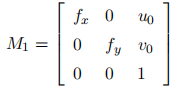
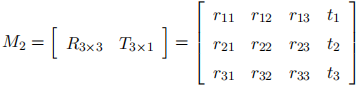
上式中，M1 为相机内参，包括相机的焦距，光轴与图像平面的焦点位置等内部参数，和外部因素无关，因此称为内参，表示为：

M2 为相机外参，表征世界坐标系到相机坐标系的转换关系，是相机在世界坐标系下的位置姿态矩阵，认为是摄像机的外参，一般情况下，如果世界坐标系设置为相机坐标系，即二者重合，那么这个外参就是一个单位矩阵。

用一张图来总结，如图1.4所示。

图 1.4: 相机标定整套流程

1.2.2 镜头畸变

实际使用中，得到的图像并不是完全按照小孔成像原理进行透视投影，通过透镜后物点在实际的成像平面上的像与理想成像之间存在一点畸变误差。误差主要存在径向畸变和切向畸变两种。径向畸变是由于相机的透镜形状造成的，切向畸变则是整个相机的组装过程中造成的。

1.2.2.1 径向畸变

图 1.5: 径向畸变

沿着透镜的半径方向分布的畸变称为径向畸变。光线在远离透镜中心的地方比靠近中心的地方更加弯曲。径向畸变可以分为，桶形畸变和枕形畸变。如图1.5所示，从左到右分别是，正常无畸变、桶形畸变、枕形畸变。径向畸变是因为，远离透镜中心的光线比靠近透镜中心的光线更加弯曲。廉价的透镜更加严重，高端相机中并不是那么明显。光心的处的畸变为 0，距离越远畸变越大。

一般情况下，图像的径向畸变往往被描述为一个低阶多项式模型。(x, y) 是没有畸变的像素点的位置，(xdistorted, ydistorted) 是径向畸变作用后的点的位置，则二者之间存在以下变换关系：

(x, y) 是归一化的图像坐标，即坐标原点已经移动到主点，并且像素坐标除以焦距，r2 = x2 +y2。k1, k2, k3 是径向畸变系数，也属于摄像头的内参。一般使用多项式的前两项，畸变很大的相机比如鱼眼相机会使用第三项。

1.2.2.2 切向畸变

图 1.6: 切向畸变

切向畸变主要发生在相机 sensor 和镜头不平行的情况下，因为有夹角，所以光透过镜头传到图像传感器上时，成像位置发生了变化。具体原理如图1.6所示。切向畸变可以用下列公式表示：

p1, p2 是畸变系数，其他变量和径向畸变相同。

将径向畸变和切向畸变放在一起考虑，可以得到下式：

所以对于镜头畸变一共有 5 个参数 k1, k2, k3, p1, p2 需要校准，这 5 个参数和 M1 一起，都是需要标定的相机内参。opencv 输出的即便参数顺序是 k1, k2, p1, p2, k3 因为 k3 没那么重要。

作者简介

林夕，电子科技大学硕士，主要研究方向：推荐系统、自然语言处理和金融风控。希望能将算法应用在更多的行业中。

编辑：于腾凯

校对：李敏