写给零基础的前端算法入门指南,摸鱼刷一刷【递归与回溯篇】
前言
原本打算通过一篇文章介绍一下,推荐一下自己的刷题方式和刷题路线,得到一些伙伴的反馈:最好还是更加详细,面向零基础,小白这些,还有github访问速度也是一方面问题,可能图片都加载不出来。
因此,我打算分模块出几期文章,这样你只用通过文章即可了解 Chocolate 同学整体刷题汇总啦。
希望能够帮助你的春秋招。打算出的内容计划安排如下:
🐮写给零基础的前端算法入门指南,摸鱼刷一刷【栈与队列与链表篇】 🐮写给零基础的前端算法入门指南,摸鱼刷一刷【递归与回溯篇】(本期已完成🎉) 
写给零基础的前端算法入门指南,摸鱼刷一刷【栈与队列与链表篇】
写给零基础的前端算法入门指南,摸鱼刷一刷【递归与回溯前置基础篇】
🐮写给零基础的前端算法入门指南,摸鱼刷一刷【双指针与字符串篇】 🐮写给零基础的前端算法入门指南,摸鱼刷一刷【二叉树篇】 🐮写给零基础的前端算法入门指南,摸鱼刷一刷【动态规划DP篇】 🐮写给零基础的前端算法入门指南,摸鱼刷一刷【总结篇】

算法这一块到底如何准备
首先,我来简单介绍一下自己,在校打过 ACM(如果没听过,当我没说,因为没有很大价值的牌牌,铁牌,参赛证以及证书倒是一堆)
如果你知道 acm,并且参与过,对于国内前端(注意是说前端)面试的话,应该不需要花费很长的刷题时间,如果大家有想法了解我的 acm 经历的话,这个后续我会考虑在 「B 站发布一期视频」。
那么对于零基础的小白来说,可能需要花 10-20 天左右时间来准备算法,而对于非科班来说这个周期可能会更长一点。那么,现在我准备来分享我是如何带你零基础刷题的。
第一点,不要畏惧算法,理解了其实就那会事,或许你还会喜欢上做题,当然,对于 acm 大佬做的题就另当别论了,这篇文章主体与面试水平为准 第二点,前端对于算法这一块的考察相对来说会偏简单一点,我在春秋招过程中遇到的笔试题都是一些常见的题目,比如搜索,贪心,简单动态规划,经典排序算法,都是以 leetcode一些简单以及中等难度的居多,而这些算法对于科班来说的话,应该在学校都学习过,比如算法分析与设计,数据结构与算法这一类课程,那么有这个基础,你的刷题时间又可以进行缩短了第三点,既然说到要刷题,该如何刷,我在掘金参考了几个大佬(文末有参考处),大家都会推荐分专题来刷,在这里,我也是非常推荐的,在这里,我希望的是将刷算法题的数量再减少一点,带你入门,当你刷完这些专题之后,你就有相关思维能力主动去刷题了,而不是很被动的去刷,这样也很方便自己总结归纳~ 其它,可以参考大佬的文章,这里不再赘述...
一份思维导图,让你的刷题路线更简单
开门见山地说,首先提供一份思维导图,让知识由繁到简。
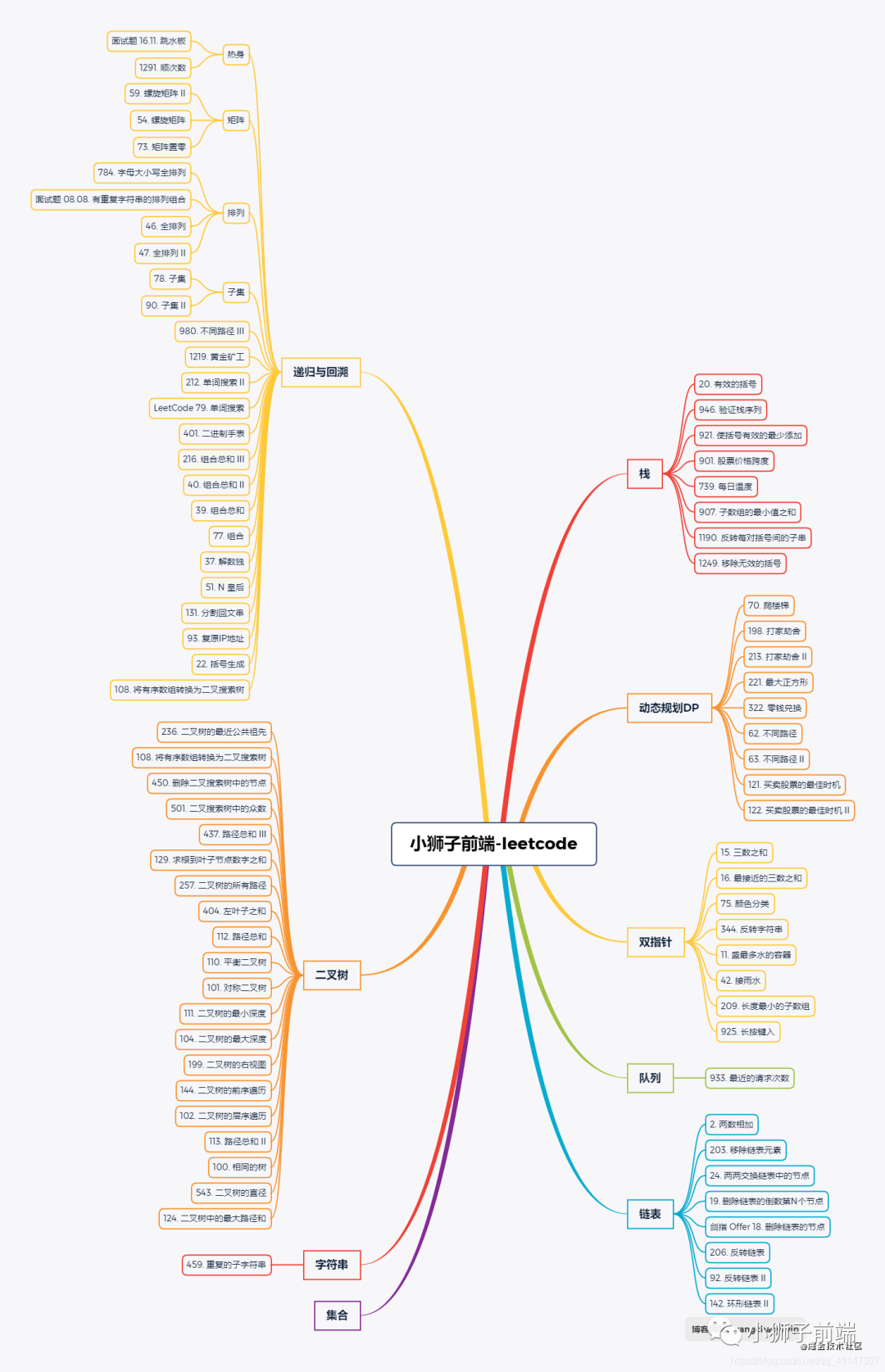
获取高清PDF,请在微信公众号「小狮子前端」回复「LeetCode」,一起刷题或者交流可在后台回复「交流」
本仓库刷题路线参考 ssh (给大佬点赞)
感谢大佬的归纳总结,原本打算在大佬那里打卡学习,后面考虑不太友好,还是自己新建了一个仓库打卡学习。
其次,本仓库解题代码大部分是自己的代码风格,题量也进行了拓展,将会持续更新下去,何不 star 收藏一下?
仓库介绍
仓库地址:https://github.com/Chocolate1999/leetcode-javascript
本仓库将全程使用的语言是 JavaScript,是一个纯前端刷题路线,对于前端刷题没有方向的小伙伴简直是福音。解题代码会记录在本仓库的 Issues 中,会按照 label进行分类。比如想查看 「递归与回溯」 分类下的问题,那么选择标签进行筛选即可。
同时,小伙伴们可以在 Issues 中提交自己的解题代码,🤝 欢迎 Contributing ,可打卡刷题,坚持下来的人最酷!Give a ⭐️ if this project helped you !
刷题路线
下面正式开始我们的刷题之路,给本篇文章来个「点赞+在看」,拿出自己心仪的键盘,开始!
以下专题顺序仅个人以及面试高频点来总结的刷题方式,大家可以根据自己的想法来组合。更多题集请参考本仓库哈~
递归与回溯

784. 字母大小写全排列
「题目描述」
给定一个字符串S,通过将字符串S中的每个字母转变大小写,我们可以获得一个新的字符串。返回所有可能得到的字符串集合。
示例:
输入:S = "a1b2"
输出:["a1b2", "a1B2", "A1b2", "A1B2"]
输入:S = "3z4"
输出:["3z4", "3Z4"]
输入:S = "12345"
输出:["12345"]
提示:
S 的长度不超过12。
S 仅由数字和字母组成。
「解题思路」
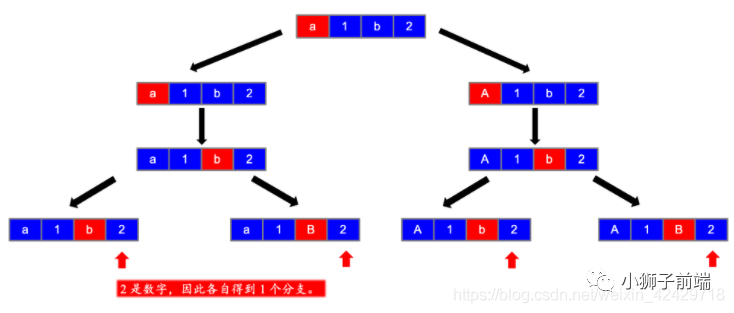
这道题就是递归操作,没有回溯,是一个挺有意思的题目,在讲解思路之前,我先搬运一下大佬的图解,方便我后续补充。
参考大佬 liweiwei1419 图解
第一步 第二步
第二步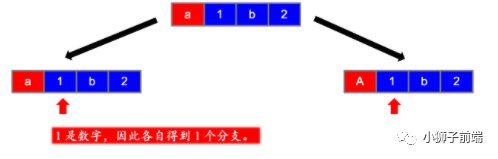 第三步
第三步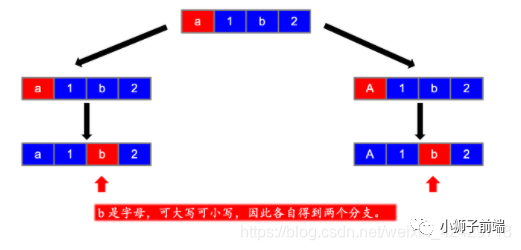 第四步
第四步
 第五步
第五步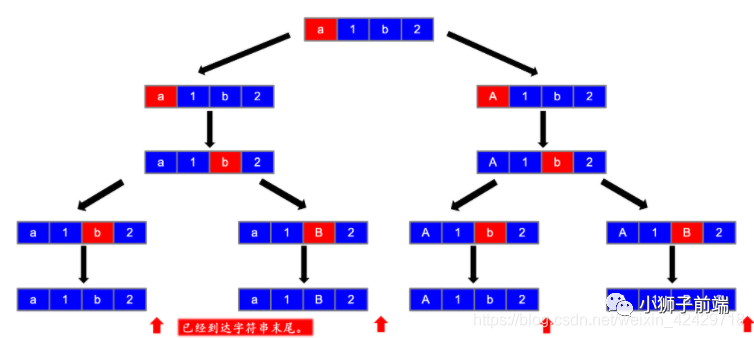 第六步
第六步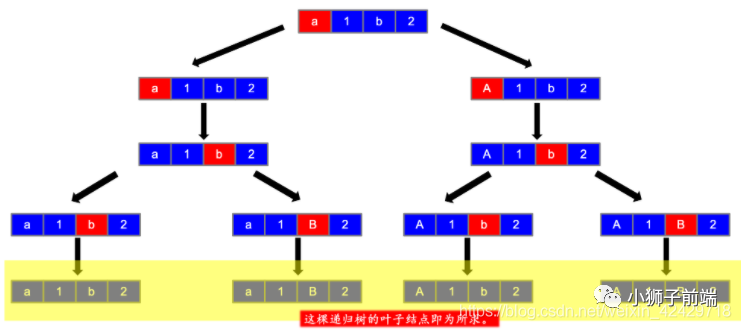 好了,有了上述图解之后(还是感谢大佬的图解,万分感谢orz),我相信明白的已经明白了,如果不明白我继续解释。
好了,有了上述图解之后(还是感谢大佬的图解,万分感谢orz),我相信明白的已经明白了,如果不明白我继续解释。
此题我们只需要从头往后遍历一遍即可,对于非字母节点,我们只会产生一个分支,而对于字母节点,我们可以产生两个分支,即大写字母和小写字母。(详细请参见下述代码)
于是,我们只要简单搜一遍就可以了。
/**
* @param {string} S
* @return {string[]}
*/
var letterCasePermutation = function(S) {
let res = []
let dfs = (t,str) => {
if(t.length === S.length)
return res.push(t)
let ch = str[0]
let nextStr = str.substr(1)
// 当前位置为数字,只有一个分支
if(!isNaN(Number(ch))){
dfs(t+ch,nextStr)
}else{
//当前位置为字母,会产生两个分支
let tmp = ch.toUpperCase()
if(tmp === ch) tmp = ch.toLowerCase()
dfs(t+ch,nextStr)
dfs(t+tmp,nextStr)
}
}
dfs('',S)
return res
};
面试题 08.08. 有重复字符串的排列组合
「题目描述」
有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
示例1:
输入:S = "qqe"
输出:["eqq","qeq","qqe"]
示例2:
输入:S = "ab"
输出:["ab", "ba"]
提示:
字符都是英文字母。
字符串长度在[1, 9]之间。
「解题思路」
全排列,直接用回溯法即可,数据量比较小,暴力完事~
var permutation = function (S) {
let res = new Set()
let vis = []
let dfs = (t) => {
if (t.length === S.length) return res.add(t)
for (let i = 0; i < S.length; i++) {
if (vis[i]) continue
vis[i] = true
dfs(t + S[i])
vis[i] = false
}
}
dfs('')
return [...res]
}
980. 不同路径 III
「题目描述」
在二维网格 grid 上,有 4 种类型的方格:
1 表示起始方格。且只有一个起始方格。2 表示结束方格,且只有一个结束方格。0 表示我们可以走过的空方格。-1 表示我们无法跨越的障碍。返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
示例 1:
输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出:2
解释:我们有以下两条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:
输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出:4
解释:我们有以下四条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:
输入:[[0,1],[2,0]]
输出:0
解释:
没有一条路能完全穿过每一个空的方格一次。
请注意,起始和结束方格可以位于网格中的任意位置。
提示:
1 <= grid.length * grid[0].length <= 20
「解题思路」
回溯算法,不过这道题需要我们走完所有空格,所以我们起初遍历的时候需要统计一下空格的数目,然后还有一个注意点就是重点也算是可走的路径的一个点,也需要统计进去,所以代码 cnt 值 初始化为 1
接下来就是回溯过程了,写了一个 check 函数,进行简单判断剪枝,然后就是往四个方向搜,每走一个格子就将当前格子设置为障碍(即 -1),然后搜索完后,回溯时,需要将障碍重设置为空格。
/**
* @param {number[][]} grid
* @return {number}
*/
var uniquePathsIII = function(grid) {
let cnt = 1 // 统计地图中可走的方格个数,包括终点,故初始值为1
let sx,sy // 记录起点坐标
for(let i=0;i<grid.length;i++){
for(let j=0;j<grid[0].length;j++){
if(grid[i][j] === 1){
sx = i
sy = j
}
else if(grid[i][j] === 0){
cnt++
}
}
}
return dfs(sx,sy,cnt,grid)
};
// 剪枝条件
let check = (sx,sy,grid) => {
if(sx<0 || sx>=grid.length || sy<0 || sy>=grid[0].length || grid[sx][sy] == -1) return false
return true
}
let dfs = (sx,sy,cnt,grid) => {
if(!check(sx,sy,grid)) return 0
if(grid[sx][sy] === 2){ // 走到终点时,也要判断一下当前所有空格是否走完
return cnt === 0 ? 1:0
}
let res = 0
grid[sx][sy] = -1 //走过的空格进行标记,设置为障碍即可
res += dfs(sx+1,sy,cnt-1,grid) // 四个方向进行搜索
res += dfs(sx,sy+1,cnt-1,grid)
res += dfs(sx-1,sy,cnt-1,grid)
res += dfs(sx,sy-1,cnt-1,grid)
grid[sx][sy] = 0 // 回溯过程,不影响后续dfs
return res
}
1219. 黄金矿工
「题目描述」
你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量;如果该单元格是空的,那么就是 0。
为了使收益最大化,矿工需要按以下规则来开采黄金:
每当矿工进入一个单元,就会收集该单元格中的所有黄金。矿工每次可以从当前位置向上下左右四个方向走。每个单元格只能被开采(进入)一次。不得开采(进入)黄金数目为 0 的单元格。矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
示例 1:
输入:grid = [[0,6,0],[5,8,7],[0,9,0]]
输出:24
解释:
[[0,6,0],
[5,8,7],
[0,9,0]]
一种收集最多黄金的路线是:9 -> 8 -> 7。
示例 2:
输入:grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出:28
解释:
[[1,0,7],
[2,0,6],
[3,4,5],
[0,3,0],
[9,0,20]]
一种收集最多黄金的路线是:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。
提示:
1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100
最多 25 个单元格中有黄金。
「解题思路」
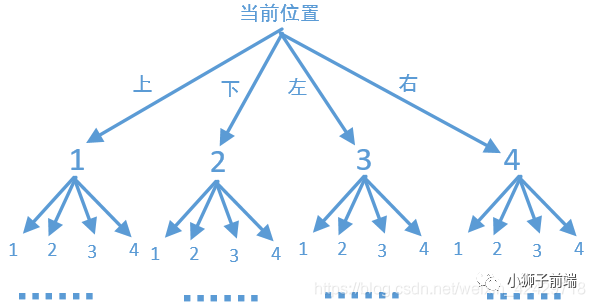
这题也是搜索相关,四个方向,不允许重复,不过这次我们需要从不同起点搜索,而且为了减少搜索次数,我们得从黄金数量不为0的点开始搜。然后每当走不下去的时候,就比较一下当前黄金数量,求出最大值即可。
/**
* @param {number[][]} grid
* @return {number}
*/
var getMaximumGold = function(grid) {
if(!grid || !grid.length) return 0
let vis = []
// 最终收集的最多黄金数量
let maxGold = 0
for(let i=0;i<grid.length;i++) vis[i] = []
// 剪枝条件
let check = (x,y) => {
if(x<0 || x>=grid.length || y<0 || y>=grid[0].length || vis[x][y] === 1 || !grid[x][y]) return false
return true
}
let dfs = (x,y,total) => {
if(check(x,y)){
vis[x][y] = 1 //防止重复
dfs(x+1,y,total+grid[x][y]) // 四个方向搜索
dfs(x,y+1,total+grid[x][y])
dfs(x-1,y,total+grid[x][y])
dfs(x,y-1,total+grid[x][y])
vis[x][y] = 0
}else{
// 走到底了,就比较一下当前黄金数量
maxGold = Math.max(maxGold,total)
}
}
// 起点从非0单元格开始
for(let i=0;i<grid.length;i++){
for(let j=0;j<grid[0].length;j++){
if(grid[i][j]){
dfs(i,j,0)
}
}
}
return maxGold
};
79. 单词搜索
「题目描述」
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
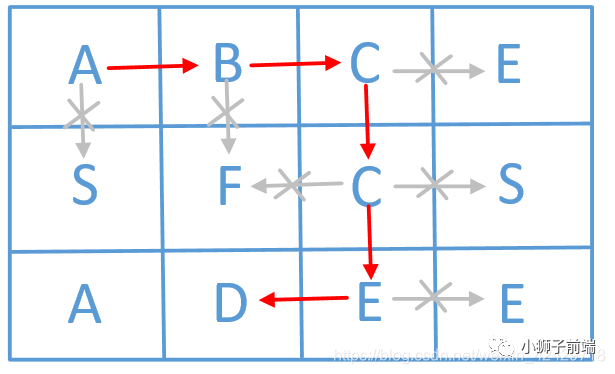
board =
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false
提示:
board 和 word 中只包含大写和小写英文字母。
1 <= board.length <= 200
1 <= board[i].length <= 200
1 <= word.length <= 10^3
「解题思路」
上一期做了单词搜索2 hard 版本之后,这道题也想用字典树玩一玩,没想到超时了,后面一想,数据确实有点大,而且对于一个单词来说,建立一颗字典树岂不是很浪费,还要花时间码代码...
本题也是回溯的思路,不过期间做了一点小优化,还是通过动态更改当前所走的格子,省去了那份 开辟vis 数组的空间。
对于递归层次,由于最后一次计算时,层次多算了一次(即多加了一次),所以条件为 >。
var exist = function(grid, word) {
let dfs = (x,y,t) => {
// 最后一次还会 +1 因此,条件是大于
if(t > word.length-1){
return true
}
// 剪枝条件
if(x<0 || x>=grid.length || y<0 || y>=grid[0].length || grid[x][y]!= word[t] || grid[x][y] == '#') return false
let tmp = grid[x][y]
// 开始走
grid[x][y] = '#'
// 从四个方向搜索,只要一个方向搜索有结果,那么直接返回 true即可
let res = dfs(x+1,y,t+1) || dfs(x,y+1,t+1) || dfs(x-1,y,t+1) || dfs(x,y-1,t+1)
if(res) return true
// 回溯(重置)
grid[x][y] = tmp
return false
}
for(let i=0;i<grid.length;i++){
for(let j=0;j<grid[0].length;j++){
if(grid[i][j] == word[0]){
let res = dfs(i,j,0)
if(res) return true
}
}
}
return false
};
212. 单词搜索 II
「题目描述」
给定一个二维网格 board 和一个字典中的单词列表 words,找出所有同时在二维网格和字典中出现的单词。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例:
输入:
words = ["oath","pea","eat","rain"] and board =
[
['o','a','a','n'],
['e','t','a','e'],
['i','h','k','r'],
['i','f','l','v']
]
输出: ["eat","oath"]
说明:
你可以假设所有输入都由小写字母 a-z 组成。
提示:
你需要优化回溯算法以通过更大数据量的测试。你能否早点停止回溯?
如果当前单词不存在于所有单词的前缀中,则可以立即停止回溯。什么样的数据结构可以有效地执行这样的操作?散列表是否可行?为什么? 前缀树如何?如果你想学习如何实现一个基本的前缀树,请先查看这个问题: 实现Trie(前缀树)。
「解题思路」
「参考力扣官网分析:实现 Trie (前缀树)」
判断是否找到了,通过传递节点的END来判断
判断是否重复访问,通过动态更改走过的网格点来判断,就不需要再定义一个
vis数组了
「参考大佬:秦时明月字典树建树解法(二)」
var findWords = function(grid, words) {
// 存放最终结果集
let res = []
// 字典树节点
class TrieNode {
constructor(){
this.end = false
this.child = {}
}
}
// 最终形成的字典树根节点
let root = null
let Trie = function(){
root = new TrieNode()
}
// 建立字典树
Trie.prototype.insert = (word) => {
let cur = root
for(let i=0;i<word.length;i++){
if(!cur.child[word[i]]){
cur.child[word[i]] = new TrieNode()
}
cur = cur.child[word[i]]
}
cur.end = true
}
// 创建根节点
let trie = new Trie()
// 进行建树操作
for(let i=0;i<words.length;i++){
trie.insert(words[i])
}
let dfs = (x,y,t,cur) => {
if(cur.end){
res.push(t)
cur.end = false // 避免重复计算
}
// 剪枝条件:1.边界处理 2.下一步是否可走 3.下一步字典树是否可走
if(x<0 || x>=grid.length || y<0 || y>=grid[0].length || grid[x][y] == '#' || !cur.child[grid[x][y]]) return
let tmp = grid[x][y]
grid[x][y] = '#' // 走
cur = cur.child[tmp]
dfs(x+1,y,t+tmp,cur) // 上下左右四个方向遍历
dfs(x,y+1,t+tmp,cur)
dfs(x-1,y,t+tmp,cur)
dfs(x,y-1,t+tmp,cur)
grid[x][y] = tmp // 回溯(还原)
}
// 对单词表进行全局搜索
for(let i=0;i<grid.length;i++){
for(let j=0;j<grid[0].length;j++){
dfs(i,j,'',root)
}
}
return res
};
附上完整字典树(前缀树)模板,日后可用~
「在 Trie 树中查找键」
每个键在 trie 中表示为从根到内部节点或叶的路径。我们用第一个键字符从根开始,。检查当前节点中与键字符对应的链接。有两种情况:
存在链接。我们移动到该链接后面路径中的下一个节点,并继续搜索下一个键字符。 不存在链接。若已无键字符,且当前结点标记为 isEnd,则返回true。否则有两种可能,均返回false: 还有键字符剩余,但无法跟随Trie树的键路径,找不到键。没有键字符剩余,但当前结点没有标记为isEnd。也就是说,待查找键只是Trie树中另一个键的前缀。
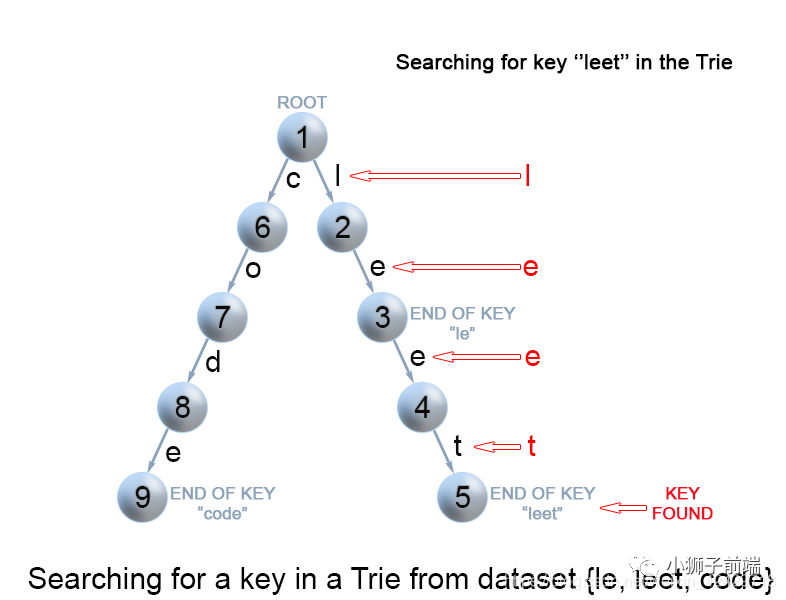 「查找 Trie 树中的键前缀」
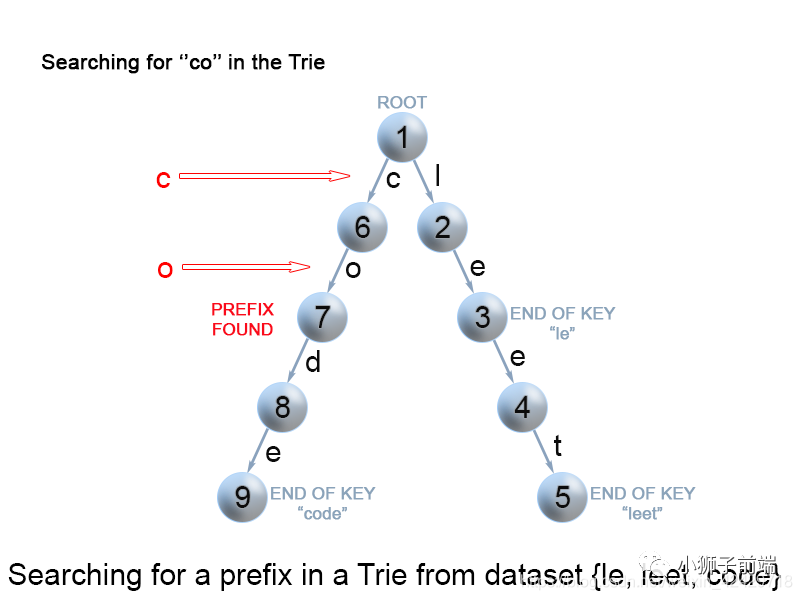
「查找 Trie 树中的键前缀」
该方法与在 Trie 树中搜索键时使用的方法非常相似。我们从根遍历 Trie 树,直到键前缀中没有字符,或者无法用当前的键字符继续 Trie 中的路径。与上面提到的“搜索键”算法唯一的区别是,到达键前缀的末尾时,总是返回 true。我们不需要考虑当前 Trie 节点是否用 “isend” 标记,因为我们搜索的是键的前缀,而不是整个键。
var findWords = function(grid, words) {
// 存放最终结果集
let res = []
// 字典树节点
class TrieNode {
constructor(){
this.end = false
this.child = {}
}
}
// 最终形成的字典树根节点
let root = null
let Trie = function(){
root = new TrieNode()
}
// 建立字典树
Trie.prototype.insert = (word) => {
let cur = root
for(let i=0;i<word.length;i++){
if(!cur.child[word[i]]){
cur.child[word[i]] = new TrieNode()
}
cur = cur.child[word[i]]
}
cur.end = true
}
// 在 Trie 树中查找键
let searchPrefix = (word) => {
let cur = root
for(let i=0;i<word.length;i++){
if(cur.child[word[i]]){
cur = cur.child[word[i]]
}else{
return null
}
}
return cur
}
Trie.prototype.search = (word) => {
let cur = searchPrefix(word)
return cur !== null && cur.end
}
// 查找 Trie 树中的键前缀
Trie.prototype.startsWith = (pre) => {
return searchPrefix(pre) != null
}
// 创建根节点
let trie = new Trie()
// 进行建树操作
for(let i=0;i<words.length;i++){
trie.insert(words[i])
}
let dfs = (x,y,t,cur) => {
if(cur.end){
res.push(t)
cur.end = false // 避免重复计算
}
// 剪枝条件:1.边界处理 2.下一步是否可走 3.下一步字典树是否可走
if(x<0 || x>=grid.length || y<0 || y>=grid[0].length || grid[x][y] == '#' || !cur.child[grid[x][y]]) return
let tmp = grid[x][y]
grid[x][y] = '#' // 走
cur = cur.child[tmp]
dfs(x+1,y,t+tmp,cur) // 上下左右四个方向遍历
dfs(x,y+1,t+tmp,cur)
dfs(x-1,y,t+tmp,cur)
dfs(x,y-1,t+tmp,cur)
grid[x][y] = tmp // 回溯(还原)
}
// 对单词表进行全局搜索
for(let i=0;i<grid.length;i++){
for(let j=0;j<grid[0].length;j++){
dfs(i,j,'',root)
}
}
return res
};
77. 组合
「题目描述」
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
「解题思路」
直接套用组合题解题模板即可
var combine = function (n, k) {
let res = [];
let dfs = (t, start) => {
if (t.length === k) {
res.push(t);
return;
}
for (let i = start; i <= n; i++) {
t.push(i);
dfs(t.slice(), i + 1);
t.pop();
}
}
dfs([], 1);
return res;
};
39. 组合总和
「题目描述」
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
提示:
1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500
「解题思路」
这道题是组合题,但是这道题有意思的是当前元素可以重复无限制选取,那么我们可以改一下另外一道组合题的思路,下一层也从 i开始即可,然后本题元素重复,那么我们不需要进行排序然后剪枝了。
// 当前元素可以无限制选取,下一层也从i开始取
dfs(t.slice(),i,sum+candidates[i]);
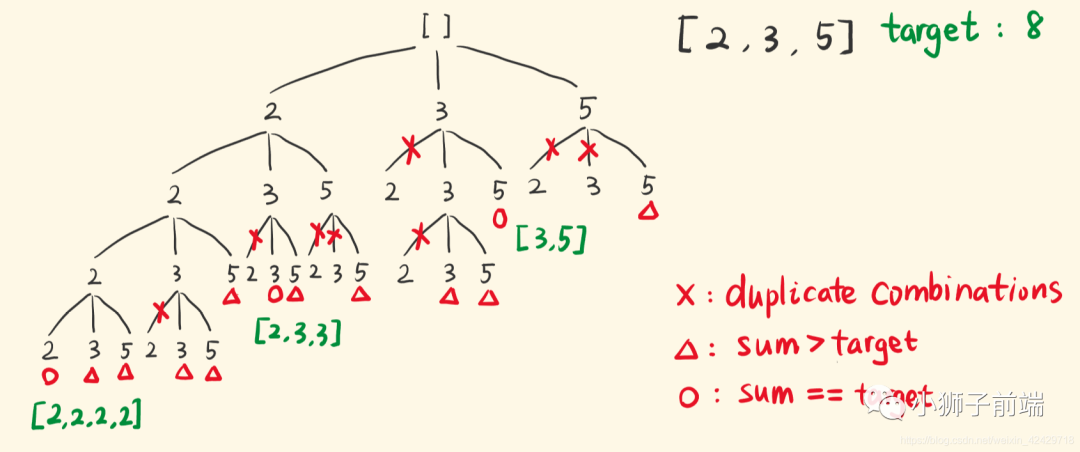
「参考xiao_ben_zhu图解」
var combinationSum = function(candidates, target) {
let res = [];
let dfs = (t,start,sum) => {
if(sum >= target){ // 防止爆掉
if(sum === target){
res.push(t);
}
return;
}
for(let i=start;i<candidates.length;i++){
t.push(candidates[i]);
// 当前元素可以无限制选取,下一层也从i开始取
dfs(t.slice(),i,sum+candidates[i]);
t.pop();
}
}
dfs([],0,0);
return res;
};
40. 组合总和 II
「题目描述」
给定一个数组 candidates和一个目标数 target ,找出candidates 中所有可以使数字和为target的组合。
candidates中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。解集不能包含重复的组合。示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
「解题思路」
这道题也是一道组合题,但是这道题数组里面是存在重复元素的,组合题的话,为了更好地去重,我们可以先对数组进行排序,然后对于每一层如果相邻元素相同,就剪掉该分支即可。
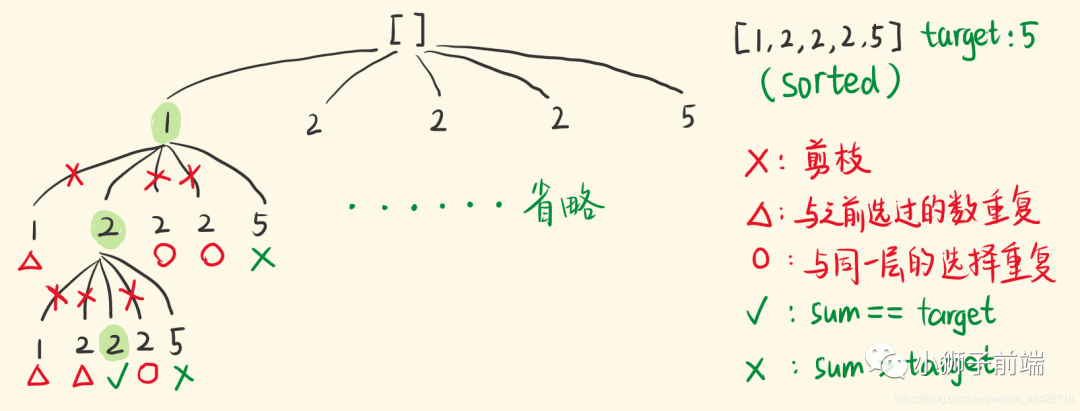
「参考xiao_ben_zhu大佬图解」
注意求和那里,如果只判断是否相等的话,可能会出现爆掉情况。
var combinationSum2 = function (candidates, target) {
let res = [];
candidates.sort((a, b) => a - b);
let dfs = (t, start, sum) => {
if (sum >= target) { // 加这外层,超出范围了也终止,防爆栈
if (sum === target) {
res.push(t);
}
return;
}
// 组合
for (let i = start; i < candidates.length; i++) {
// 组合元素不能重复,去掉同一层重复的元素
if (i > start && candidates[i] == candidates[i - 1]) continue;
t.push(candidates[i]);
// 组合元素去重,即当前选择和下一层的不能重复
dfs(t.slice(), i + 1, sum + candidates[i]);
t.pop();
}
}
dfs([], 0, 0);
return res;
};
216. 组合总和 III
「题目描述」
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。解集不能包含重复的组合。示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
「解题思路」
首先,还是搬运一下大佬的图解,然后我再来解释一番。
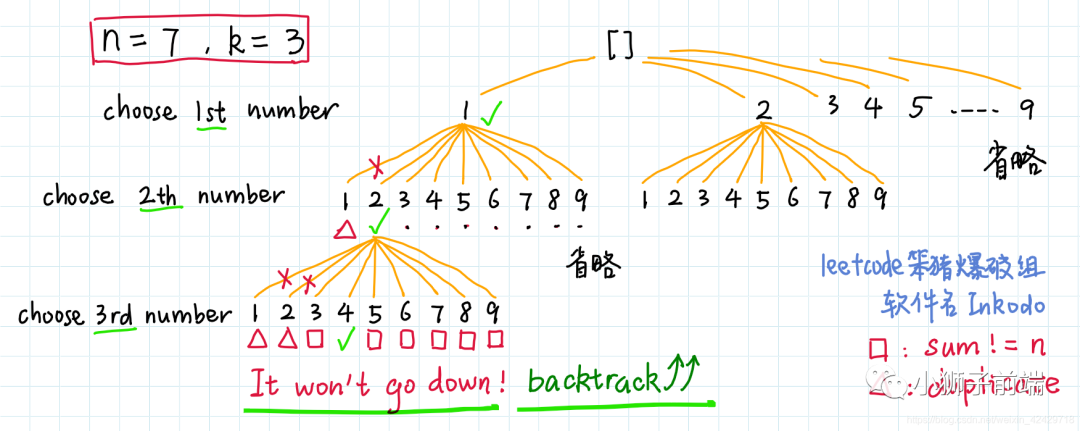
「参考xiao_ben_zhu大佬图解」
本题需要一层一层来,第一层我们可以有 i(1-9)个选择,而第二层的每一个值只有 i+1个选择了,因为不能重复。比如你第一次拿了 2,在下一次,你只能从 3开始拿了,如果还是 1的话就会有重复的组合了。这样我们也不用维护 vis数组来去重,因为每一层取的值是不一样的。
var combinationSum3 = function (k, n) {
let res = [];
let dfs = (t, start, sum) => {
if (t.length === k && sum === n) {
res.push(t);
}
for (let i = start; i < 10; i++) {
t.push(i);
dfs(t.slice(), i + 1, sum + i);
t.pop();
}
}
dfs([], 1, 0);
return res;
};
401. 二进制手表
「题目描述」
二进制手表顶部有 4 个 LED 代表 「小时(0-11)」,底部的 6 个 LED 代表 「分钟(0-59)」。
每个 LED 代表一个 0 或 1,最低位在右侧。

例如,上面的二进制手表读取 “3:25”。
给定一个非负整数 n 代表当前 LED 亮着的数量,返回所有可能的时间。
示例:
输入: n = 1
返回: ["1:00", "2:00", "4:00", "8:00", "0:01", "0:02", "0:04", "0:08", "0:16", "0:32"]
提示:
输出的顺序没有要求。
小时不会以零开头,比如 “01:00” 是不允许的,应为 “1:00”。
分钟必须由两位数组成,可能会以零开头,比如 “10:2” 是无效的,应为 “10:02”。
超过表示范围(小时 0-11,分钟 0-59)的数据将会被舍弃,也就是说不会出现 "13:00", "0:61" 等时间。
「解题思路」
回溯算法,我的解法类似于全排列做法,将10个小灯泡进行排列组合,然后根据 0 和 1 来判断灯泡是否亮,如果亮了,加上对应二进制,然后将 0-3分给小时来计算,将 4-9分给分钟来计算,但是要考虑一下,就是可能会出现重复情况,于是用 Set数据结构维护一下就好了。
var readBinaryWatch = function(num) {
let res = new Set();
let vis = new Array(10).fill(0)
let check = (hour,minutes) => {
if(hour>=0 && hour<=11 && minutes>=0 && minutes<=59) return true;
return false;
}
let dfs = (t,vis) => {
if(t==0){
let hour = vis[0]*1 + vis[1]*2 + vis[2]*4 + vis[3]*8;
let minutes = vis[4]*1 + vis[5]*2 + vis[6]*4 + vis[7]*8 + vis[8]*16 + vis[9]*32;
if(check(hour,minutes)){
let tmp = `${hour}:${minutes >= 10? minutes: '0'+minutes}`;
res.add(tmp);
}
}
for(let i=0;i<10;i++){
if(vis[i]) continue;
vis[i] = 1;
dfs(t-1,vis);
vis[i] = 0;
}
}
dfs(num,vis);
return [...res];
};
补充,后面看到有大佬这样做,进行了去重操作,关键点在回溯 for循环那里。其实这个相当于全排列了。
var readBinaryWatch = function(num) {
let res = [];
let vis = new Array(10).fill(0)
let check = (hour,minutes) => {
if(hour>=0 && hour<=11 && minutes>=0 && minutes<=59) return true;
return false;
}
let dfs = (t,cnt,vis) => {
if(t==0){
let hour = vis[0]*1 + vis[1]*2 + vis[2]*4 + vis[3]*8;
let minutes = vis[4]*1 + vis[5]*2 + vis[6]*4 + vis[7]*8 + vis[8]*16 + vis[9]*32;
if(check(hour,minutes)){
let tmp = `${hour}:${minutes >= 10? minutes: '0'+minutes}`;
res.push(tmp);
}
return;
}
for(let i=cnt;i<=10-t;i++){
if(vis[i]) continue;
vis[i] = 1;
dfs(t-1,i+1,vis);
vis[i] = 0;
}
}
dfs(num,0,vis);
return res;
};
37. 解数独
「题目描述」
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需「遵循如下规则」:
数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。空白格用 '.' 表示。
 一个数独。
一个数独。
 答案被标成红色。
答案被标成红色。
提示:
给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。
「解题思路」
我们一行一行的放,如果能得到一个解,直接返回 true,然后剪枝条件如下述 check函数。
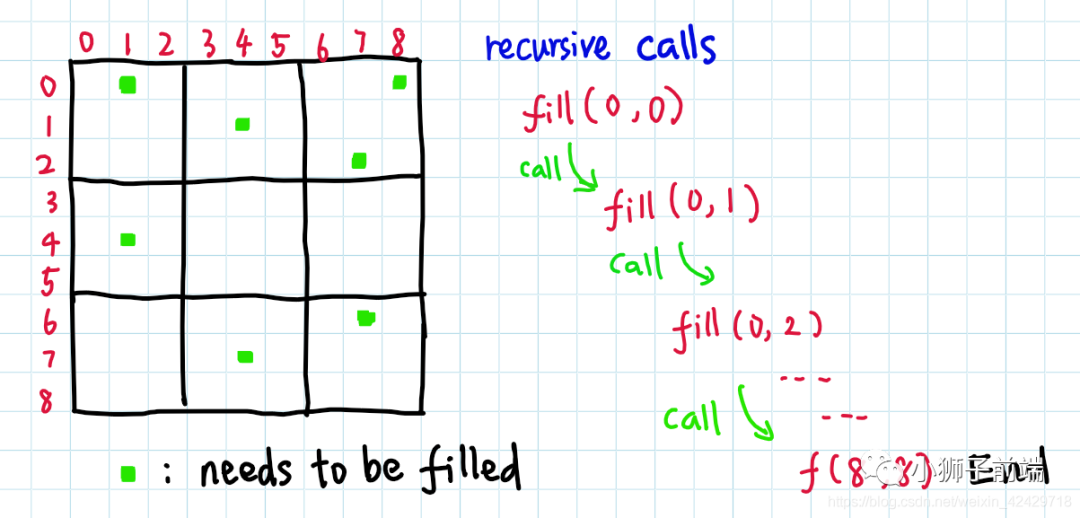
「参考xiao_ben_zhu大佬图解」
var solveSudoku = function (board) {
let check = (x, y, val) => {
// 一行或者一列有重复元素,剪掉
for (let i = 0; i < 9; i++) {
if (board[x][i] == val || board[i][y] == val) return true;
}
let xx = Math.floor(x / 3) * 3;
let yy = Math.floor(y / 3) * 3;
// 3x3宫格内重复的情况,剪掉
for (let i = 0; i < 3; i++) {
for (let j = 0; j < 3; j++) {
if (board[xx + i][yy + j] == val) return true;
}
}
return false; // 没有冲突情况
}
let dfs = (x, y) => {
if (y == 9) {
x++;
y = 0;
if (x == 9) return true; // 都填完了,直接返回 true
}
if (board[x][y] != '.') return dfs(x, y + 1);
for (let i = 1; i < 10; i++) {
if (check(x, y, String(i))) continue;
board[x][y] = String(i);
if (dfs(x, y + 1)) return true; // 如果往下走,能够解出数独,直接返回 true
board[x][y] = '.'; // 回溯,因为往下走得不到一个解
}
return false;
}
dfs(0, 0);
return board;
};
51. N 皇后
「题目描述」
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。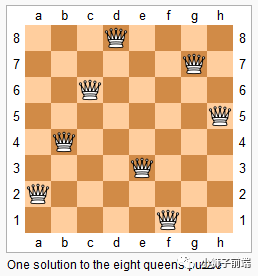
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例:
输入:4
输出:[
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
提示:
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
「解题思路」
对于 n 皇后问题,经典的回溯算法,我们采用一行放一个,然后逐行来放,这样我们就不用在剪枝的时候判断是否同行了。只需要判断是否同列 或者 同一斜线就好了。
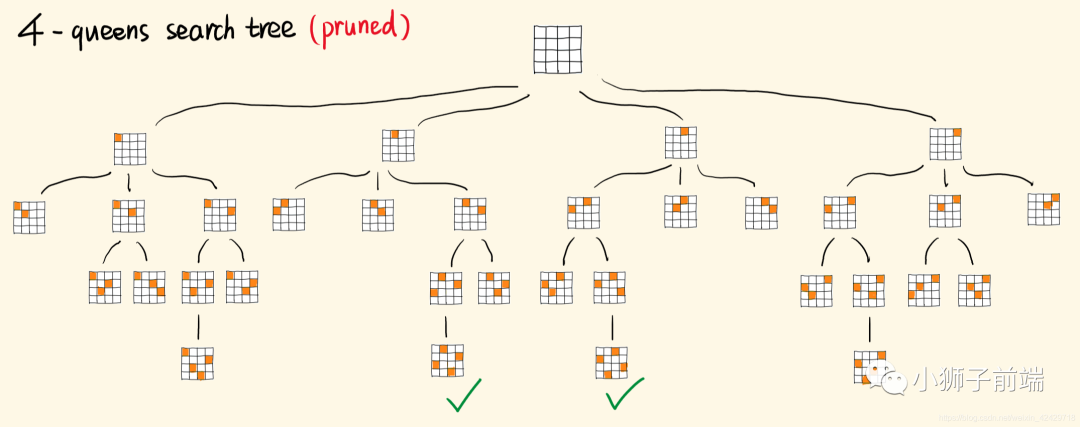
参考「xiao_ben_zhu」大佬图解
var solveNQueens = function(n) {
let res = [];
let grid = new Array(n); // 初始化一个地图
for(let i=0;i<n;i++){
grid[i] = new Array(n).fill('.');
}
// 剪枝条件
let check = (x,y)=>{
for(let i=0;i<x;i++){
for(let j=0;j<n;j++){
// 判断同列 或者 同一斜线即可(不需要判断同行是因为一行一行放的,一定不同行)
if(grid[i][j] == 'Q' && (j == y || i+j == x+y || i-j == x-y) ){
return true;
}
}
}
return false;
}
let dfs = (t) => {
if(t === n ){
let ans = grid.slice(); // 拷贝一份,对输出做处理
for(let i=0;i<n;i++){
ans[i] = ans[i].join('');
}
res.push(ans);
return;
}
for(let i=0;i<n;i++){
if(check(t,i)) continue;
grid[t][i] = 'Q';
dfs(t+1);
grid[t][i] = '.';
}
}
dfs(0);
return res;
};
131. 分割回文串
「题目描述」
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
「解题思路」
借鉴「zesong-wang-c」 大佬的图解
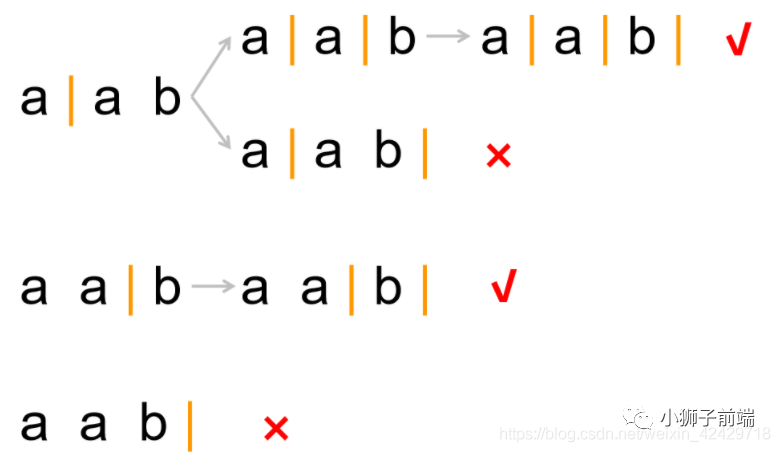
本题采用回溯思想,看上图基本已经明白,每次进行一次切割,直到切到最后一个元素,然后压入结果集合里,期间对于每次切割的字符串,我们判断一下是否是回文,如果不是,直接减掉即可。
和组合的思想有点类似。
// 判断是否是回文
function isPal(str) {
let len = Math.floor(str.length / 2);
if (len === 0) {
return true;
}
let add = str.length % 2 === 0 ? 0 : 1;
let subStr = str.slice(0, len);
for (let i = 0; i < len; i++) {
if (subStr[len - i - 1] !== str[len + add + i]) {
return false;
}
}
return true;
}
var partition = function (s) {
let res = [];
let dfs = (cur, start) => {
// 当前已经到达了最后一个元素
if (start >= s.length) {
res.push(cur.slice());
return;
}
for (let i = start; i < s.length; i++) {
// 字符串切割
let str = s.slice(start, i + 1);
if (str && isPal(str) ) {
cur.push(str);
dfs(cur, i + 1);
// 回溯
cur.pop();
}
}
}
dfs([], 0);
return res;
};
93. 复原IP地址
「题目描述」
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
示例 3:
输入:s = "1111"
输出:["1.1.1.1"]
示例 4:
输入:s = "010010"
输出:["0.10.0.10","0.100.1.0"]
示例 5:
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
提示:
0 <= s.length <= 3000
s 仅由数字组成
「解题思路」
直接看图解,显然要用回溯来做,我的做法是对于当前位置,我们可以有三种选择,选一个,选两个,还有选三个。此时就需要判断一下是不是会出现选出边界的情况。
然后对于我们选择的数字,要判断是否出现前导 0 ,同时也要看一下如果是三位数字的话,是不是会超过 255 。题目不能重复选择,于是用组合思想,免去 vis 数组。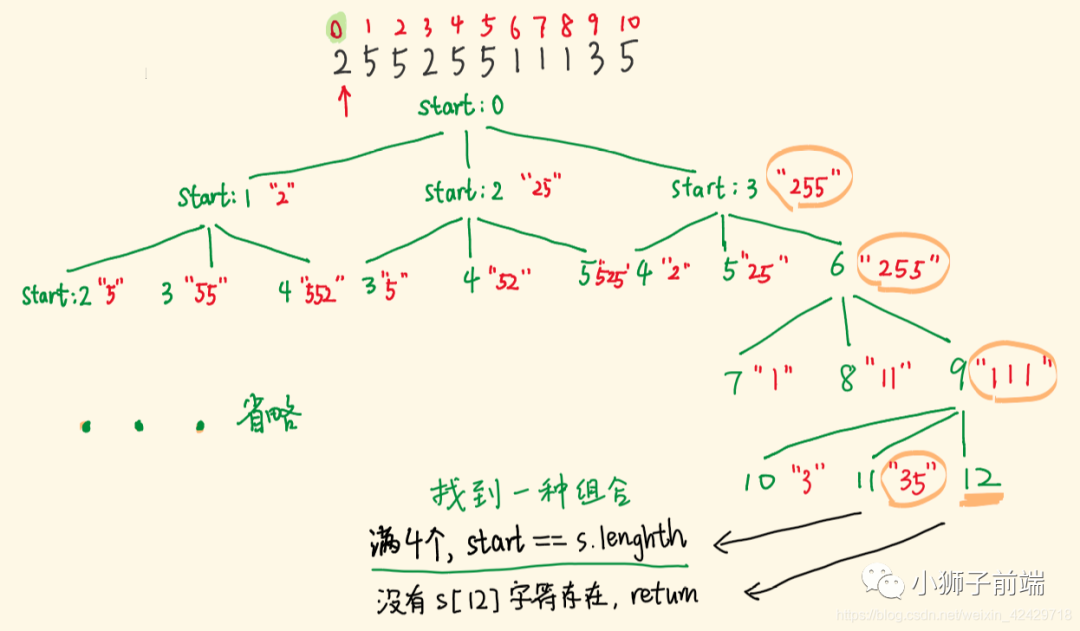 借助大佬 xiao_ben_zhu 图解
借助大佬 xiao_ben_zhu 图解
var restoreIpAddresses = function (s) {
let res = [];
let dfs = (cur, start) => {
if (cur.length == 4 && start>=s.length) {
res.push(cur.join('.'));
return;
}
if(cur.length == 4 && start != s.length) return;
for(let k=1;k<=3;k++){
// 如果取的范围超过了字符串长度,直接剪掉
if(start+k-1>=s.length) return;
// 切割字符串
let str = s.substring(start,start+k);
if(str.length>=2 && str[0] == 0) return;
if(str.length>=3 && +str > 255) return;
cur.push(str);
dfs(cur.slice(),start+k);
// 回溯
cur.pop();
}
}
dfs([], 0);
return res;
};
22. 括号生成
「题目描述」
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
「解题思路」
这道题,看了大佬的题解,发现真是有意思,现在来解释一下。
我们可以直接走可行的情况,对于不可行的情况,自然就剪掉了。
关键在于左右括号如何选择,首先,对于左括号,起初我们必然是要选的,然后我们也可以全部选完,因此,只要有左括号我们必须选,而对于右括号而言,它的剩余数量必须大于剩余左括号数量,我们才能选右括号。
举个反例,假如我们现在已经有了 (()),n = 3,然后左右括号都还剩一个,如果理解选 ),岂不是就 (()))了,显示不是有效的括号,应该被剪掉才是,因此,我们必须严格右括号剩余数量必须大于剩余左括号数量,我们才能选右括号。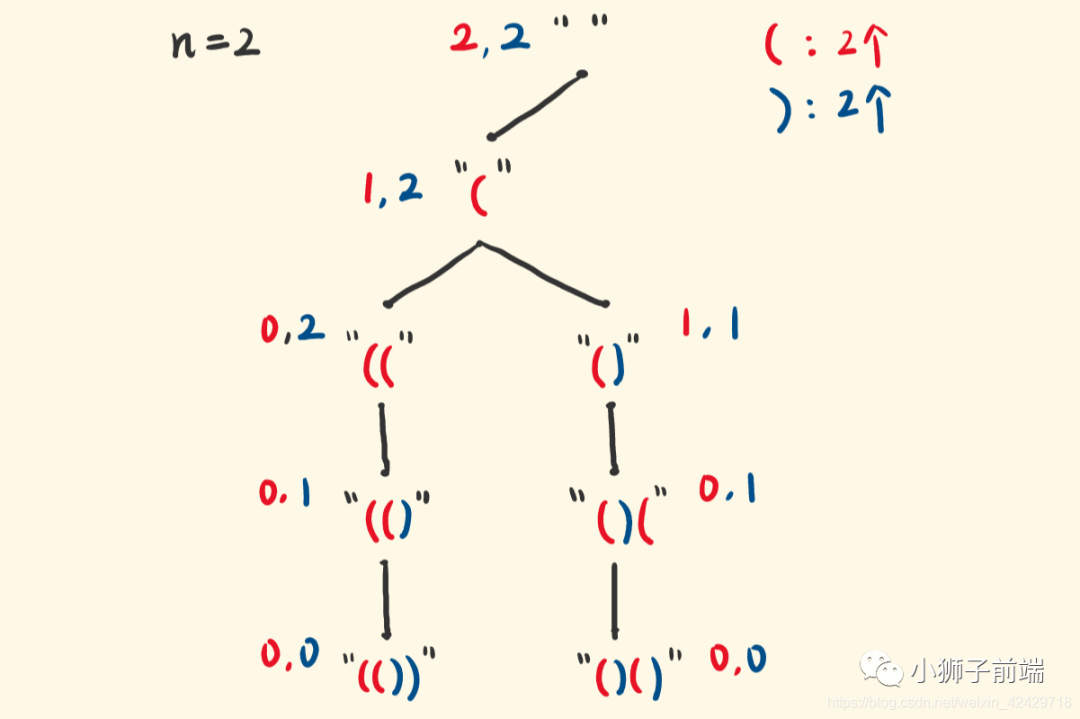 参考 笨猪爆破组 大佬图解
参考 笨猪爆破组 大佬图解
var generateParenthesis = function (n) {
let res = [];
let dfs = (cur, left, right) => {
if (cur.length === 2 * n) {
res.push(cur);
return;
}
// 左括号还存在,就可以选左括号
if (left > 0) dfs(cur + '(', left - 1, right);
// 右括号数量要大于左括号,才可以选右括号
if (right > left) dfs(cur + ')', left, right - 1);
}
dfs('', n, n);
return res;
};
本文参考
「前端该如何准备数据结构和算法?」 「写给前端的算法进阶指南,我是如何两个月零基础刷200题」 「(1.8w字)负重前行,前端工程师如何系统练习数据结构和算法?【上】」
参考链接:
结语
❤️关注+点赞+收藏+评论+转发❤️,原创不易,您的支持将会是我最大的动力~
祝愿在准备春秋招の你,能够早点结束,offer 拿到手软,希望我的文章能够帮助到你,我们很快会在下期相遇,给个赞及时催更呀~
学如逆水行舟,不进则退
你若喜欢,为小狮子点个【在看】哦~
