又一个数学大模型开源了~
大模型家族来了一个专门解决数学问题的「新成员」——Llemma。
如今,在各种文本混合数据上训练出来的语言模型会显示出非常通用的语言理解和生成能力,可以作为基础模型适应各种应用。开放式对话或指令跟踪等应用要求在整个自然文本分布中实现均衡的性能,因此更倾向于通用模型。
不过如果想要在某一领域(如医学、金融或科学)内最大限度地提高性能,那么特定领域的语言模型可能会以给定的计算成本提供更优越的能力,或以更低的计算成本提供给定的能力水平。
普林斯顿大学、 EleutherAI 等的研究者为解决数学问题训练了一个特定领域的语言模型。他们认为:首先,解决数学问题需要与大量的专业先验知识进行模式匹配,因此是进行领域适应性训练的理想环境;其次,数学推理本身就是 AI 的核心任务;最后,能够进行强数学推理的语言模型是许多研究课题的上游,如奖励建模、推理强化学习和算法推理。
因此,他们提出一种方法,通过对 Proof-Pile-2 进行持续的预训练,使语言模型适应数学。Proof-Pile-2 是数学相关文本和代码的混合数据。将这一方法应用于 Code Llama,可以得到 LLEMMA:7B 和 34B 的基础语言模型,其数学能力得到了大幅提高。

论文地址:https://arxiv.org/pdf/2310.10631.pdf
项目地址:https://github.com/EleutherAI/math-lm
LLEMMA 7B 的 4-shot Math 性能远超谷歌 Minerva 8B,LLEMMA 34B 在参数少近一半的情况下性能逼近 Minerva 62B。
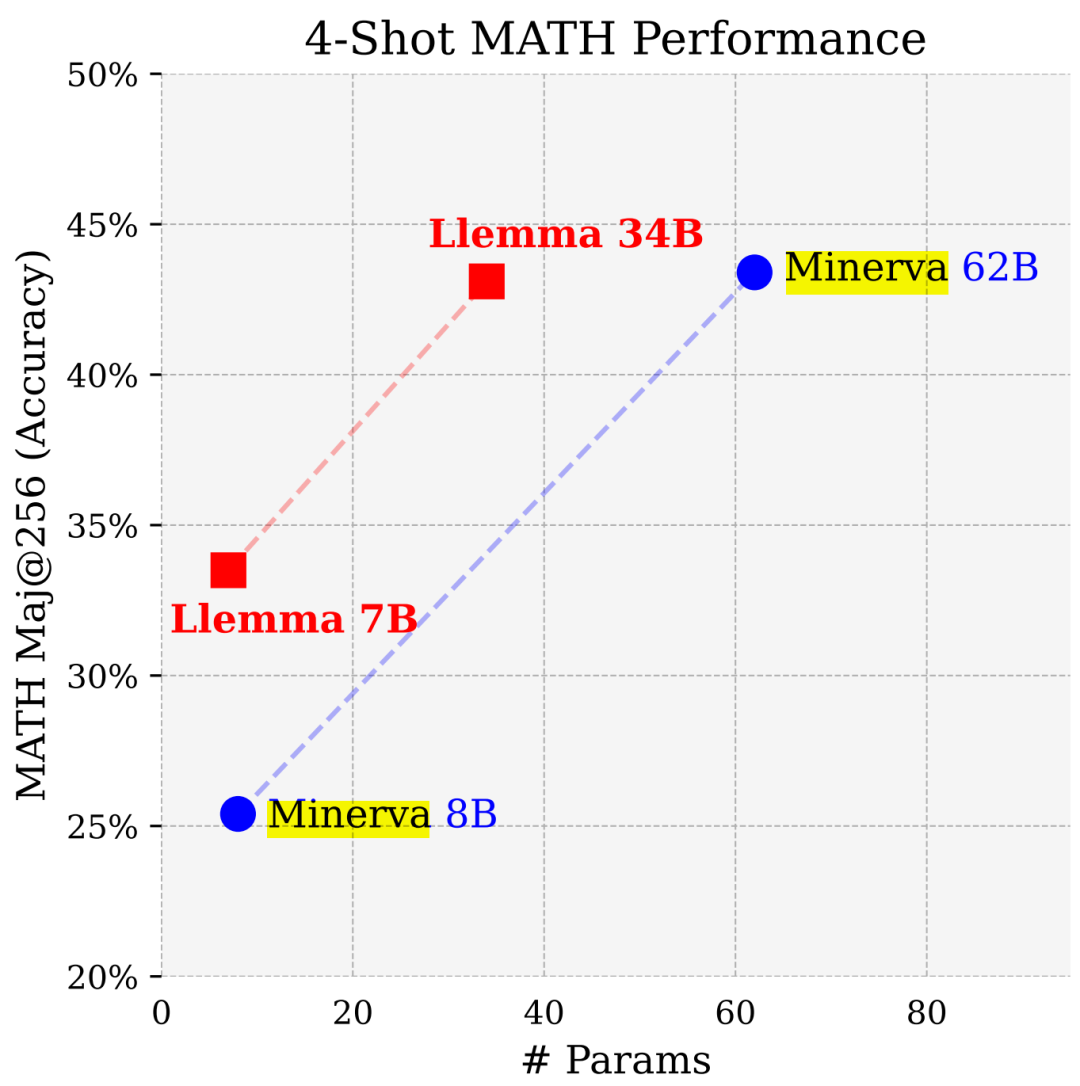
具体来说,本文贡献如下:
-
1. 训练并发布了 LLEMMA 模型:专门用于数学的 7B 和 34B 语言模型。LLEMMA 模型是在 MATH 上公开发布的基础模型的最新水平。 -
2. 发布了代数堆栈(AlgebraicStack),这是一个包含 11B 专门与数学相关的代码 token 的数据集。 -
3. 证明了 LLEMMA 能够使用计算工具来解决数学问题,即 Python 解释器和形式定理证明器。 -
4. 与之前的数学语言模型(如 Minerva)不同,LLEMMA 模型是开放式的。研究者开放了训练数据和代码。这使得 LLEMMA 成为未来数学推理研究的一个平台。
方法概览
LLEMMA 是专门用于数学的 70B 和 34B 语言模型。它由 Proof-Pile-2 上继续对代码 Llama 进行预训练得到的。
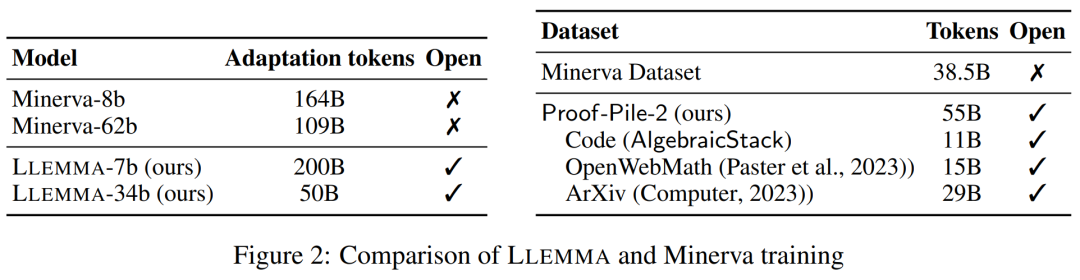
DATA: Proof-Pile-2
研究者创建了 Proof-Pile-2,这是一个 55B token 的科学论文、包含数学的网络数据和数学代码的混合物。除了 Lean proofsteps 子集之外,Proof-Pile-2 的知识截止日期为 2023 年 4 月。
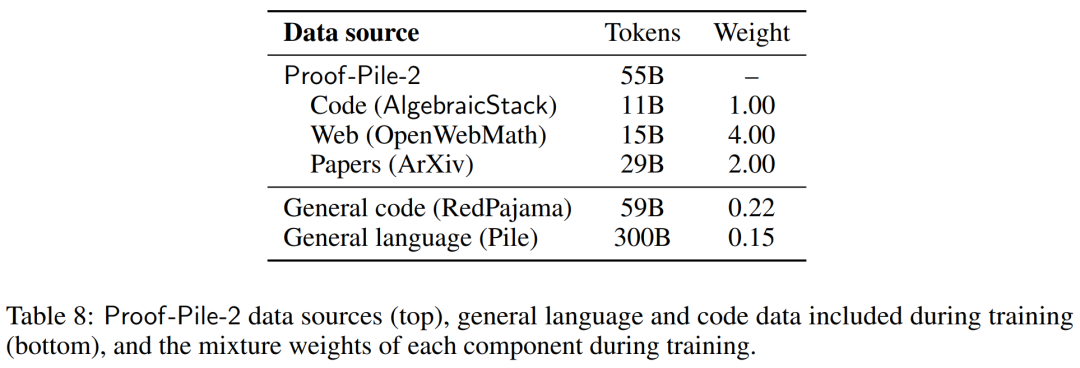
数值模拟、计算机代数系统和形式定理证明器等计算工具对数学家的重要性与日俱增。因此,研究者创建了代数堆栈(AlgebraicStack),这是一个包含 17 种语言源代码的 11B token 数据集,涵盖数值数学、符号数学和形式数学。该数据集由来自 Stack、GitHub 公共资源库和形式证明步骤数据的过滤代码组成。表9显示了AlgebraicStack 中各语言的 token 数量。
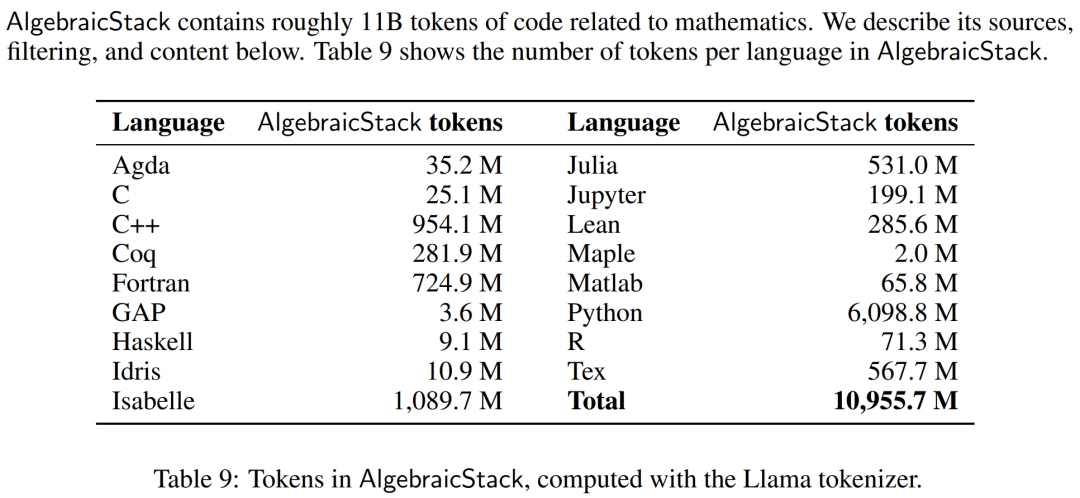
AlgebraicStack 中各语言的 token 数。
研究者了使用 OpenWebMath,这是一个由高质量网页组成的 15B token 数据集,其中过滤了数学内容。OpenWebMath 根据数学相关关键词和基于分类器的数学评分过滤 CommonCrawl 网页,保留数学格式(如 LATEX、AsciiMath),并包含额外的质量过滤器(如 plexity、domain、length)和近似重复。
除此之外,研究者还使用了 RedPajama 的 ArXiv 子集,它是 LLaMA 训练数据集的开放再现。ArXiv 子集包含 29B 个词块。训练混合数据由少量一般领域数据组成,起到了正则化的作用。由于 LLaMA 2 的预训练数据集尚未公开,研究者使用 Pile 作为替代训练数据集。
模型和训练
每个模型都是从 Code Llama 初始化而来,该模型又初始化自 Llama 2,使用仅解码器(deconder only)的 transformer 结构,在 500B 的代码 token 上训练而成。研究者使用标准自回归语言建模目标,在 Proof-Pile-2 上继续训练 Code Llama 模型。这里,LLEMMA 7B 模型有 200B token,LLEMMA 34B 模型有 50B token。
研究者使用 GPT-NeoX 库在 256 个 A100 40GB GPU 上,以 bfloat16 混合精度来训练以上两个模型。他们为 LLEMMA-7B 使用了世界大小为 2 的张量并行,为 34B 使用了世界大小为 8 的张量并行,以及跨数据并行副本的 ZeRO Stage 1 分片优化器状态。此外还使用 Flash Attention 2 来提高吞吐量并进一步降低内存需求。
LLEMMA 7B 经过了 42000 步的训练,全局 batch 大小为 400 万个 token,上下文长度为 4096 个 token。这相当于 23000 个 A100 时。学习率在 500 步后预热到了 1・10^−4,然后在 48000 步后将余弦衰减到最大学习率的 1/30。
LLEMMA 34B 经过了 12000 步的训练,全局 batch 大小同样为 400 万个 token,上下文长度为 4096。这相当于 47000 个 A100 时。学习率在 500 步后预热到了 5・10^−5,然后衰减到峰值学习率的 1/30。
评估结果
在实验部分,研究者旨在评估 LLEMMA 是否可以作为数学文本的基础模型。他们利用少样本评估来比较 LLEMMA 模型,并主要关注没有在数学任务监督样本上进行微调的 SOTA 模型。
研究者首先使用思维链推理和多数投票(majority voting)方法来评估 LLEMMA 求解数学题的能力,评估基准包括了 MATH 和 GSM8k。然后探索使用少样本工具和定理证明。最后研究了内存和数据混合的影响。
使用思维链(CoT)求解数学题
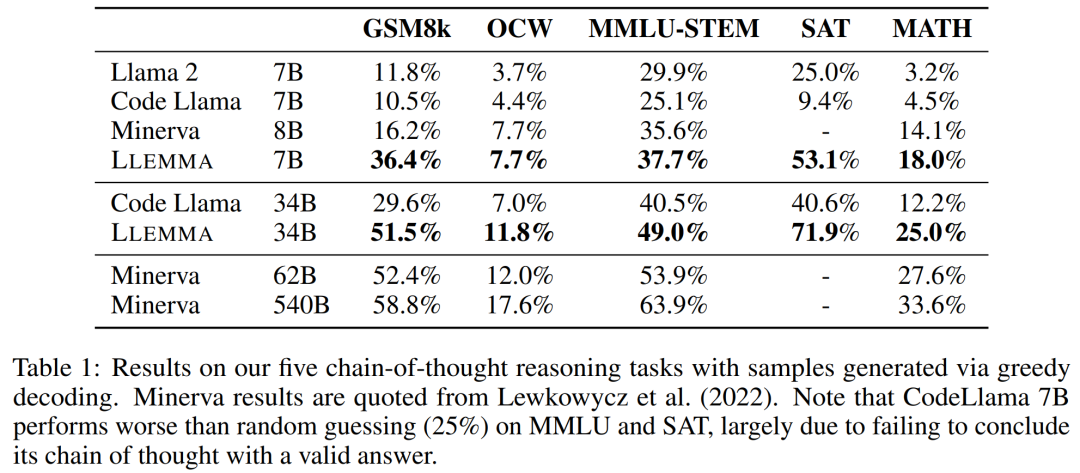
这些任务包括为 LATEX 或自然语言表示的问题生成独立的文本答案,而无需使用外部工具。研究者使用到的评估基准有 MATH、GSM8k、 OCWCourses、SAT 和 MMLU-STEM。
结果如下表 1 所示,LLEMMA 在 Proof-Pile-2 语料库上的持续预训练在 5 个数学基准上均提升了少样本性能,其中 LLEMMA 34B 在 GSM8k 上比 Code Llama 提高了 20 个百分点,在 MATH 上比 Code Llama 提高了 13 个百分点。同时 LLEMMA 7B 优于专有的 Minerva 模型。
因此,研究者得到结论,在 Proof-Pile-2 上进行持续预训练有助于提升预训练模型求解数学题的能力
使用工具求解数学题
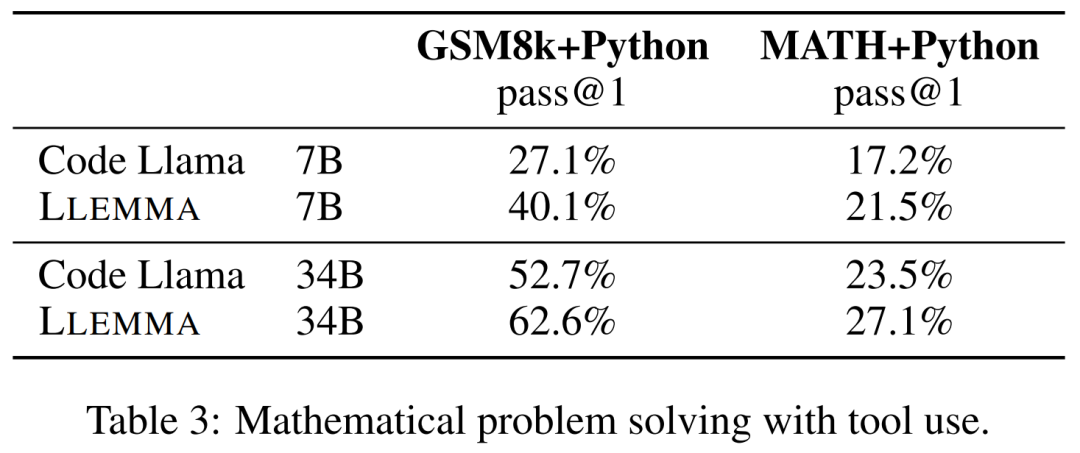
这些任务包括使用计算工具来解题。研究者使用到的评估基准有 MATH+Python 和 GSM8k+Python。
结果如下表 3 所示,LLEMMA 在这两项任务上均优于 Code Llama。同时使用工具后在 MATH 和 GSM8k 上的性能也优于没有工具的情况。
形式数学
Proof-Pile-2 的 AlgebraicStack 数据集拥有 15 亿 token 的形式数学数据,包括提取自 Lean 和 Isabelle 的形式化证明。虽然对形式数学的全面研究超出了本文的探讨范围,但研究者在以下两个任务上评估了 LLEMMA 的少样本性能。

非形式到形式证明任务,即在给定形式命题、非形式 LATEX 命题和非形式 LATEX 证明的情况下,生成一个形式证明;
形式到形式证明任务,即通过生成一系列证明步骤(或策略)来证明一个形式命题。
结果如下表 4 所示,LLEMMA 在 Proof-Pile-2 上的持续预训练在两个形式定理证明任务上提升了少样本性能。
数据混合的影响
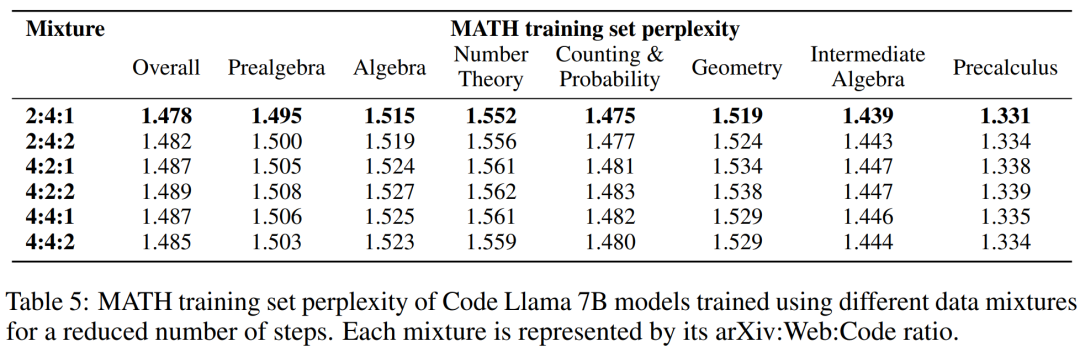
训练语言模型时,一种常见的做法是根据混合权重对训练数据的高质量子集进行上采样。研究者在几个精心挑选的混合权重上进行了短期训练,以此选择混合权重。接着选择了在一组高质量 held-out 文本(这里使用了 MATH 训练集)上能够最小化困惑度的混合权重。
下表 5 显示了使用 arXiv、web 和代码等不同数据混合训练后,模型的 MATH 训练集困惑度。
更多技术细节和评估结果参阅原论文。
本文转自机器之心
