一文看懂开源图化框架中的循环设计逻辑！

作者 Chunel Feng，编程爱好者，阿里巴巴引擎开发工程师。

个人微信：ChunelFeng
个人博客：一面之猿网^[1]
个人项目：CGraph 图计算框架^[2]

大家好，我是不会写代码的纯序员——Chunel Feng。

相信大家在日常工作中，已经精通各种循环逻辑的实现。就拿我来说吧，多年的工作经验，已经让我可以熟练的使用 C++，Python，英语等多种语言，循环多次输出“hello word”。不过大家有没有想过一个这样的问题：如何在一个有向无环图（Directed Acyclic Graph，简称dag）中实现循环呢？

今天，我们就来介绍一下如何实现这个小目标 —— 而且是想怎么循环，就怎么循环哦~~~

功能介绍

为了防止有比我还小白的童鞋，我先几句话介绍一下什么是dag。dag是一种图结构，由多个图节点组成，每个节点可以指向 0 个或 n 个其他的节点，且在图内部不会形成环形指向的结构。

如果觉得定义太枯燥，那看下面的图，哪个是dag、哪个不是dag应该就一目了然了。顺便说一句，tree结构也可以理解成是一种特殊的dag，就好比list可以理解成是一种特殊的tree一样。

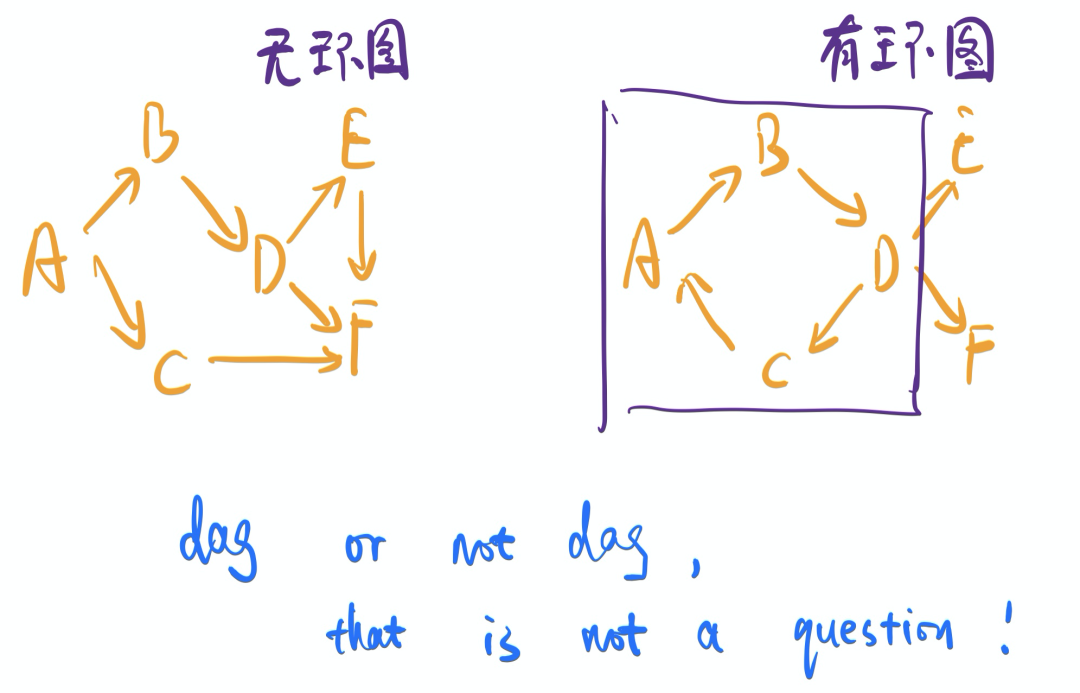
在上一篇文章中，我们介绍了图（以下内容，dag和“图”表示同一概念）中节点是按什么顺序执行的。至于图中循环，举个例子，我们假设每个节点的功能，就是输出字母。这个时候，我们需要整个流图输出一串字母：abcbcd，需要如何实现？

最常规的方法：实现一些算子，功能是输出 a,bcbc,d 即可。 假设我要输出不同的 n 次 bc，还要实现 n 个不同的算子么？有人说，可以实现一个算子，输出 bc 即可，然后循环次数可以当做参数传递进来啊。但是这样的算子，功能不是最细粒度，可重用性并不高——比如下次又需要循环输出 ab 了呢？

还有一种方法：反正可以创建节点的，我们只要实现 4 个算子分别输出 a/b/c/d，然后向图里按照顺序注册 6 个次就好了。 那问题又来了，需要 bc 反复循环 100 次怎么办？又有方法：外部写个 for 循环，注册 100 次进去啊。emmm，好像也行。那如果是需要 bc 反复输出 100 亿次呢？for 循环注册 100 亿次？

注册节点实际上是在程序内部 new 节点的过程，是需要开辟内存和分配资源的。如果你的电脑性能这么给力的话，我不建议你用来写程序。应该直接去挖比特币，用比特币的钱再去买更多的电脑，再来挖更多的比特币——当然了，这又是另一种循环了，不在我们今天的讨论范围之内，哈哈。

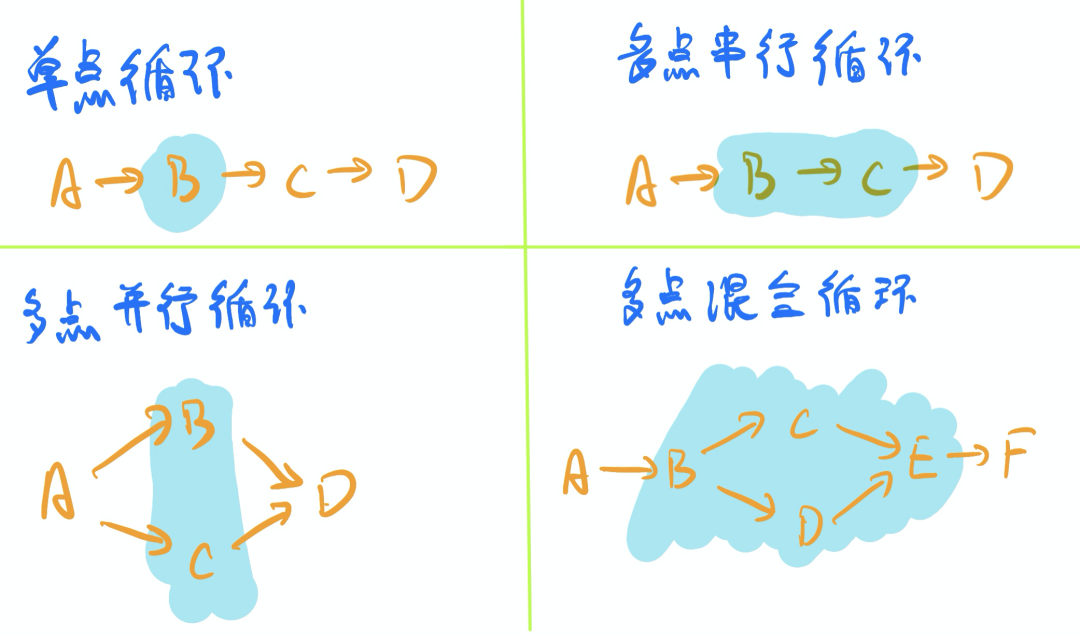
言归正传，上图中，背景为蓝色的区域，表示需要循环执行的区域。可以看出，在dag中循环主要有四种形式：单点循环，多点串行循环，多点并行循环和多点混合循环。

【单点循环】就不多解释了，见名知意。

刚才抛出的问题，实际上是多点（b、c 两个节点）【串行循环】，循环的时候，bc 需要依次顺序执行。

多点【并行循环】，指的是输出的结果 bc 需要循环多次输出，但是可以无序的情况。

至于多点【混合循环】，可以理解成循环的区域又由好几部分组成，其中的部分区域需要串行，有的部分可以并行。如图第四部分所示，循环处执行的顺序是：b->cd(或 dc)->e。

B 节点明明仅依赖 A 节点，如何让程序执行完 C 节点之后，“掉头”回来继续执行 B 呢？如何标记这些信息呢？我们接下来就结合CGraph开源项目的实现逻辑，为大家做一些通用的解释。

需要申明的是，看懂以下内容并不需要你了解 CGraph 工程本身，但需要你已经了解了dag图的执行原理。还不懂执行原理的童鞋，可以先看一下我的上一篇文章：如何实现一个图化框架？代码已开源！

名词解释

我们先梳理几个名词，说到具体流程的时候，会用得到。

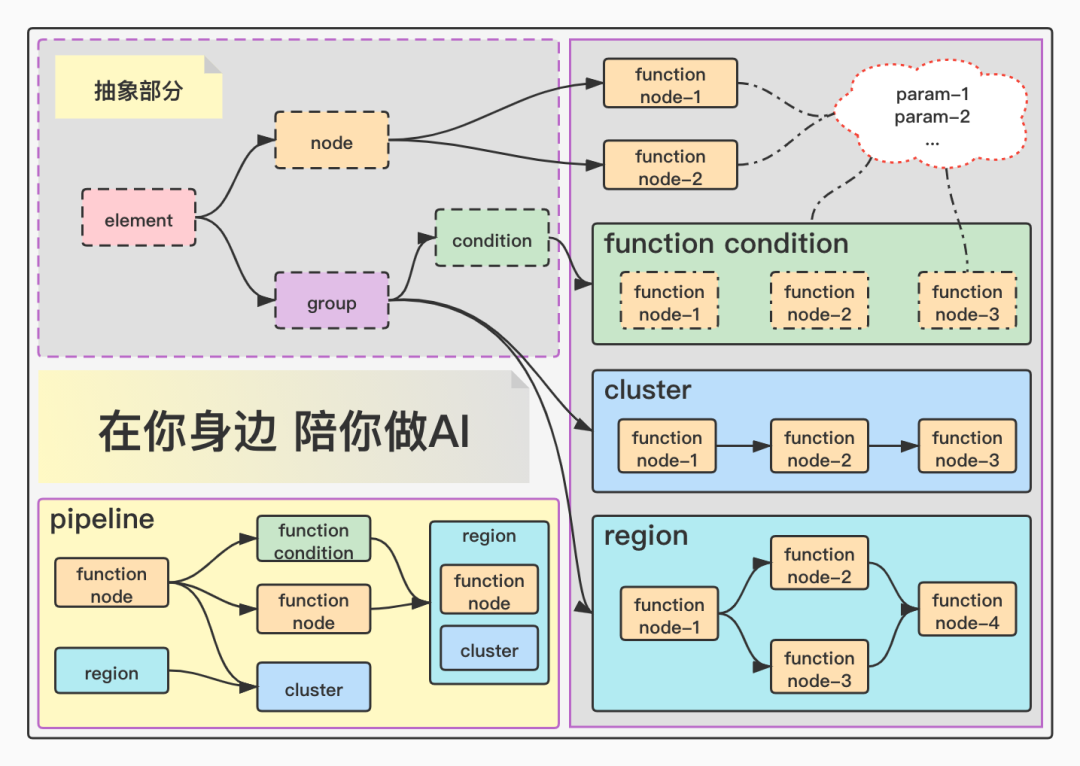
•element（元素）

element 是所有被执行结构的基类，可以派生出node,group两种类型。无实际意义，且不可被执行。

•node（节点）

node 是最小粒度的算子。node本身无法执行，但所有有具体功能的功能节点，都继承自node。

•functionNode（功能节点）

functionNode 是最小粒度的可执行算子，继承自node类，相当于是node的功能实现类。与node不同的是，functionNode有具体功能，且可以被执行。至于具体功能是什么，可以是输出字母 a，也可以是去挖比特币。总之，需要自己去实现。

•group（组）

group 是多个functionNode的组合。自身不可以执行，但可以派生出cluster和region等组合逻辑。

•cluster（簇）

cluster 继承自group，由多个functionNode线性组合而成。执行cluster的时候，内部的node依次顺序执行。简而言之就是可以依次完成多个功能。

•region（区域）

region 继承自group，也是由多个functionNode组合而成。与cluster的区别是，region中的加入的node需要指定相互依赖关系。如果不指定依赖的话，就相当于是并发执行了，因为没有任何需要依赖信息。

•pipeline（流水线）

pipeline是以上信息运行的地方。所有的functionNode、cluster、region信息，都需要注册到pipeline中，并且设定相互依赖关系。注册了以上三种信息的pipeline，实际上就对应了一个dag图，执行pipeline的过程，就是图执行的过程。

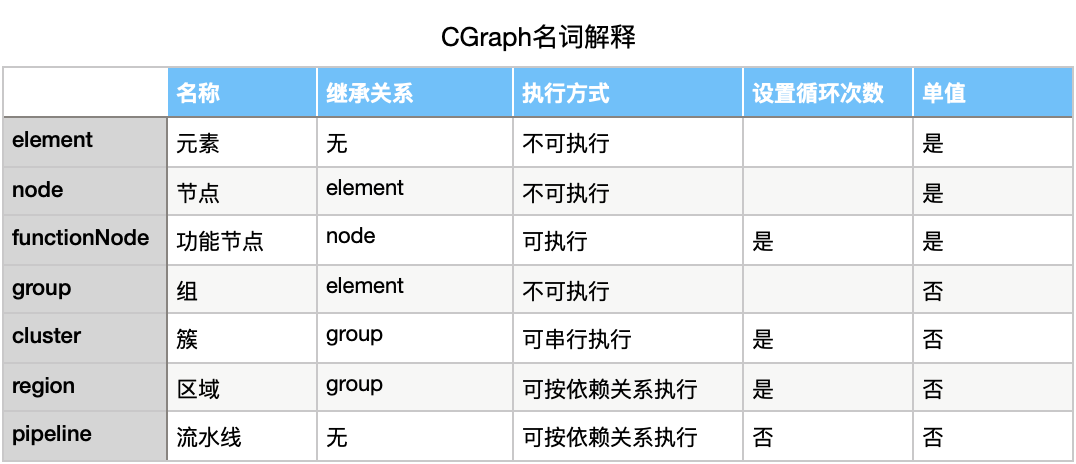
实现思路

一句话：分治！

看了上面介绍的朋友，应该已经能想到，一个图实际上是由多个不同的子模块组成。这些子模块都可以拆解成functionNode、cluster、region这三种形式，而这三种形式都统一派生自element类。在向图中注册element的时候，也可以注册这个element的循环执行次数。而不同的element，又有自己专属的执行方式，比如：functionNode就是简单执行自己的功能，而cluster就是依次执行其中的functionNode。针对cluster的循环执行，就是依次执行其中的functionNode，并且循环 n 次即可。

当然，还有更扫的。functionNode、cluster、region这三个类，实际都继承自element，那相当于是cluster中，不仅可以加入functionNode，也可以加入region甚至是另一个cluster了。而加入的信息中，又可以有自己的循环执行逻辑。region也是同理，这样就可以实现cluster中加入循环 n 次的region，region中再加入循环 m 次的内部的cluster的无限套娃逻辑了。

当然了，针对循环问题，我相信 bfs 或者 dfs 应该也是可以解决的。但是解决的过程，会相对更加吃力一些，而且流程的颗粒度没有使用分治来的清晰。有兴趣的朋友，可以自己尝试一下。

给大家带上几句 CGraph 中具体实现的代码吧。更多的例子，可以去 github 去搜索同名工程，里面还有实现了套娃逻辑的例子哦，哈哈。

#include "MyGNode/MyNode1.h"#include "MyGNode/MyNode2.h"void tutorial_cluster () {    CSTATUS status = STATUS_OK;    GPipelinePtr pipeline = new GPipeline();    GElementPtr a, b_cluster, c, d = nullptr;    b_cluster = pipeline->createGGroup<GCluster>({         pipeline->createGNode<MyNode1>(GNodeInfo("nodeB1", 1)),    // 创建名为nodeB1的node信息，并将其放入b_cluster中         pipeline->createGNode<MyNode1>(GNodeInfo("nodeB2", 3)),    // 创建名为nodeB2且自循环3次的node信息，并将其放入b_cluster中         pipeline->createGNode<MyNode2>(GNodeInfo("nodeB3", 1))    });    // 创建cluster信息，包含了三个node信息    /* 请对所有返回值进行判定 */    status = pipeline->registerGElement<MyNode1>(&a, {}, "nodeA", 1);        // 将名为nodeA的node信息，注册入pipeline中    status = pipeline->registerGElement<GCluster>(&b_cluster, {a}, "clusterB", 2);    // 将名为clusterB，依赖a执行且自循环2次的cluster信息，注册入pipeline中    status = pipeline->registerGElement<MyNode1>(&c, {a}, "nodeC", 1);    status = pipeline->registerGElement<MyNode2>(&d, {b_cluster, c}, "nodeD", 2);    status = pipeline->process();    CGRAPH_ECHO("pipeline process status is : [%d]", status);    delete pipeline;}

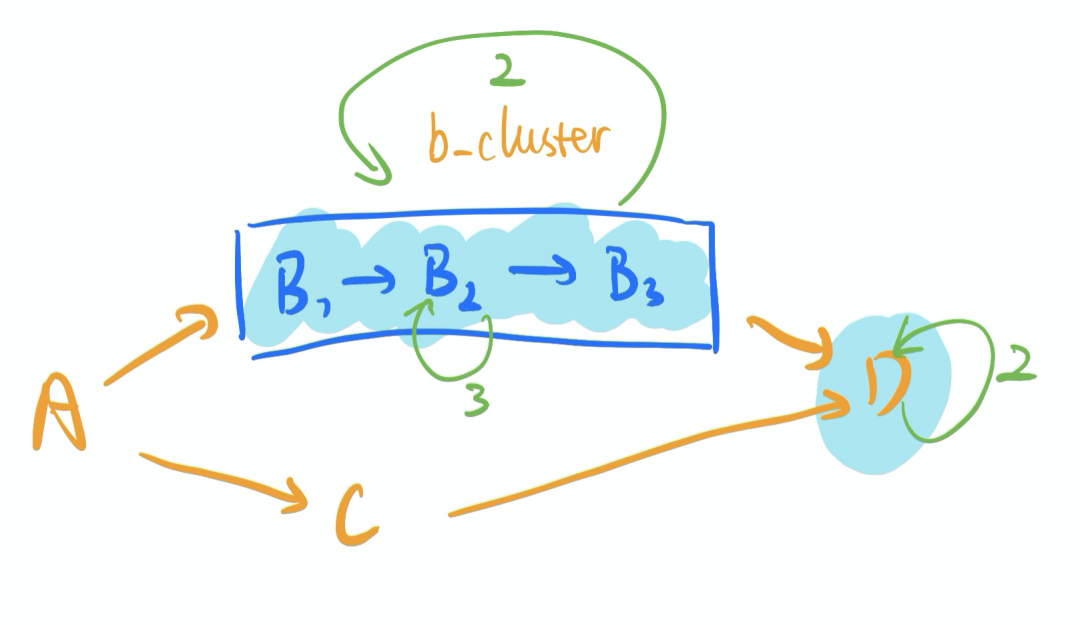
在 CGraph 中，以上几句代码，就实现了图片中描述的循环逻辑。其中，MyNode1和MyNode2是继承于node并且实现了特定功能的子类。A，B1，C等信息，都是一个functionNode。而B1，B2，B3作为一个cluster，被循环执行 2 次。每个循环的过程中，B2又自己单独循环执行 3 次，D自己循环执行 2 次。

假设A、C、D的功能是打印字母 A、C、D，而B1，B2，B3的功能是打印数字 1、2、3。那最终打印出来的结果，就是 A[1C222312223]DD，其中长串数字和 C 的输出顺序（中括号内部）每次可能不同，因为是并行执行。

写在最后

大数据和人工智能当道的时代，图化框架已然成了当下的主流。对这部分知识的了解，是很有必要加入日程的。大家熟悉的 tensorflow，flink 等库，在数据传递和计算的时候，底层都维护了一张“看不见的图”。

CGraph 项目是一个 C++的开源的并行图计算框架，最近也是刚刚起步，还有很多功能没有实现，比如跨模块参数的传递、底层并发优化、当前信息快照和异常恢复处理等等等。也希望有兴趣的朋友可以联系我们，加入我们，一起实现一点小的功能，或者测出几个 bug 啥的。生而为程序员，一起为开（bai）源(piao)社区做一点自己的贡献，提升自己的同时，也可以做到 build together, power another —— 共建，赋能。

引用链接

[1] 一面之猿网: http://www.chunel.cn/
[2] CGraph 图计算框架: https://github.com/ChunelFeng/CGraph

长按识别下图二维码，关注公众号「Doocs 开源社区」，第一时间跟你们分享好玩、实用的技术文章与业内最新资讯。