如何快速找出数组中出现一半以上的数字-轻识

题目：

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。

1 哈希表

用哈希表记录每个元素出现的次数，如果该元素出现次数超过一半，返回该元素。
时间复杂度O（n）
空间复杂度O（n）

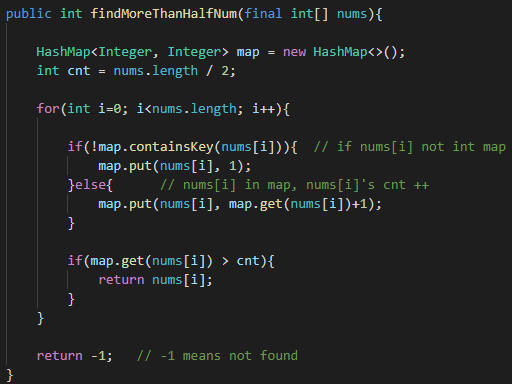
很容易看出来，该算法使用了HashMap作为额外的空间，因此该算法的空间复杂度为O(n)，我们接下来看一种空间复杂度为O(1)的算法。

2 幸存者(候选者)算法

我给这个算法起了一个比较有趣的名字，叫做幸存者(候选者)算法。基本的思路是，在遍历数组过程中，每次找到一对不相等的数，给砍掉，最后活下来的幸存者就是有可能是整个数组中出现的次数超过数组长度的一半的那个数。

例如{1,2,3,2,2,2,5,4,2}

1） 1≠2，砍掉这两个数

2）3≠2，砍掉这两个数

3）2≠5，砍掉这两个数

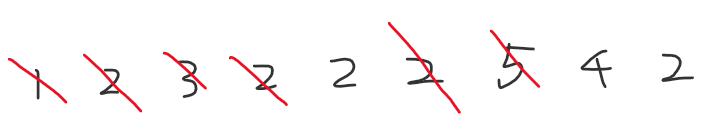
4）4≠2，砍掉这两个数

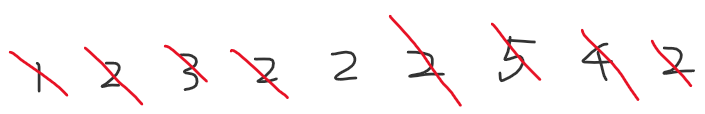
至此，没得砍了，2成为了最后的幸存者，那这个2就有可能是整个数组中出现的次数超过数组长度的一半的那个数，所以我们还要遍历一遍数组，看看2是否是真的出现一半。

那如何实现呢？该算法我觉得实在是太妙了！而且只需要遍历一遍数组就能够知道那个幸存者是哪个数字。

我们准备两个变量，cand和times，cand为候选数字，而times表示候选数字出现的次数。

1）遍历1，把cand置为1，而times也变为1(因为1这个候选人出现了一次)

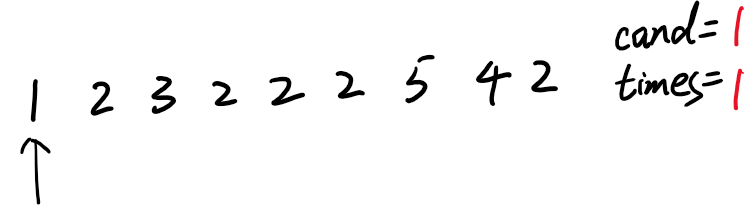
2）遍历2，发现2和cand不相等，那么我们要开砍了，怎么砍呢？只需要把times减1即可，times变为0了。在我们的潜意识里，1和2这一对不相等的数已经被砍掉了，妙吧~

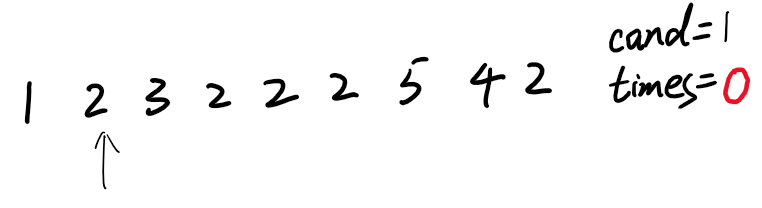
3）上一步已经把times置为0了，说明没有候选人了，当我们遍历3的时候，重新把3立为候选人。

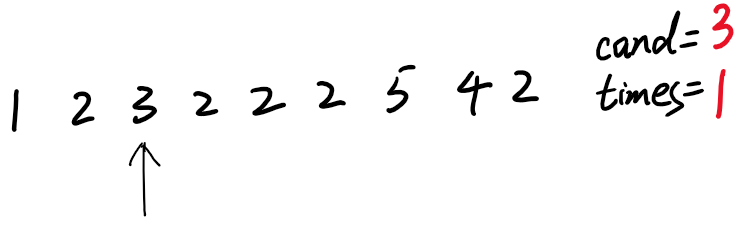
4）2≠cand(3)，砍掉，times减一。

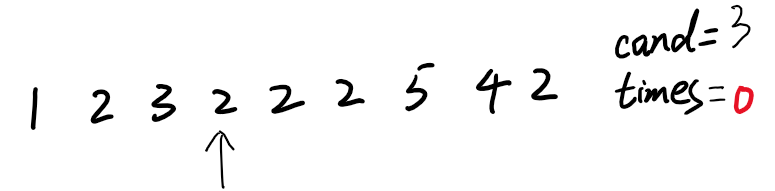
5）2重新立为候选人

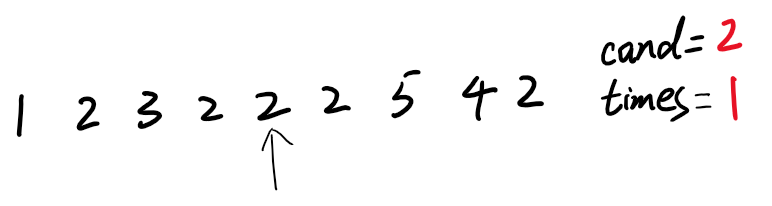
6）2这个候选人出现次数++，times变为2

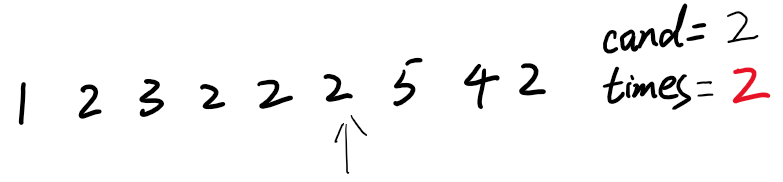
7）5≠2，砍掉，只需要将times减一即可，times变为1了，含义就是5和2都被砍掉了。

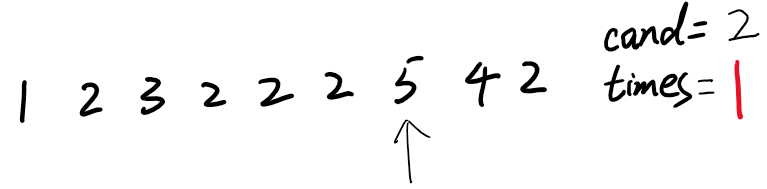
8）4≠2，砍掉，将times减一，times变为0了，候选人又没了，4和2都被砍掉了。

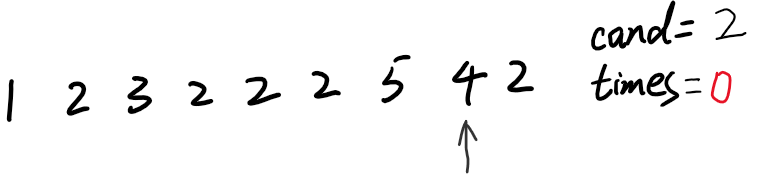
9）2重新立为候选人

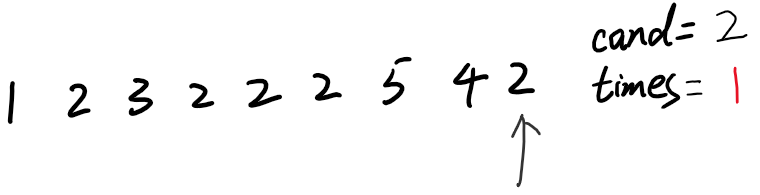
10）最后候选人为2，2就有可能是整个数组中出现的次数超过数组长度的一半的那个数

11）重新遍历一遍数组，看看2是不是真的是整个数组中出现的次数超过数组长度的一半的那个数

很明显，只需要两个变量就能完成这个任务，不需要O(n)的空间复杂度啦。

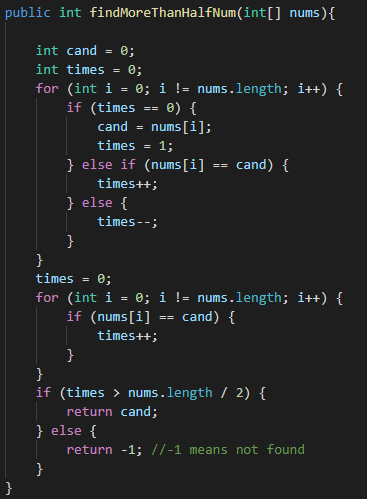
完1