无需深度学习即可提取图像特征-轻识

全网搜集目标检测相关，人工筛选最优价值内容

编者荐语

图像分类是数据科学中最热门的领域之一，文章中分享了一些将图像转换为特征向量的技术，可以推广到每个分类模型中使用。

一、定义

VATbox，作为n一个我们所暗示的，涉及增值税问题（以及更多）的发票世界的问题之一是，我想知道有多少发票是一个形象？为了简化问题，我们将问一个二元问题，图像中是否有一张发票或同一图像中有多张发票？为什么不使用文本（例如TF-IDF）？为什么只使用图像像素作为输入？因此，有时我们没有可靠的OCR，有时OCR花费了我们金钱，我们不确定我们是否要使用它。.当然，对于本文来说，演示经典方法从图像中提取特征的力量。

import cv2gray_image = cv2.imread(image_path, 0)img = image.load_img(image_path, target_size=(self.IMG_SIZE, self.IMG_SIZE))

二、缩小图像

想象一下，你们正在密切注视着图像，可以看到附近的像素。因此，如果我们的图像包含文本，则可以看到单词之间和行之间的白色像素。如果我们的意图是（至少在这种情况下）决定图像中是否有一张发票，我们可以从一定距离看图像-这将有助于忽略图像中的“无聊”空白。

# scale parameter – the relative size of the reduced image after the reduction.image_width = int(gray_image.shape[1] * scale_percent)image_height = int(gray_image.shape[0] * scale_percent)dim = (width, height)gray_reduced_image = cv2.resize(gray_image, dim, interpolation=cv2.INTER_NEAREST)cv2.imshow('image', resized)cv2.waitKey(0)

三、图像的熵

我们可以这样考虑-每个图像的多个发票或单个发票之间的差异可以转换为图像中的信息量，因此，我们可以期望每个类别中的平均熵得分不同。

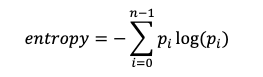
其中n是灰度级的总和（8位图像为256），p是像素具有灰度级i的概率。

from sklearn.metrics.cluster import entropyentropy1 = entropy(gray_image)entropy2 = entropy(gray_reduced_image)

四、数据库扫描

Dbscan算法具有在图像空间中查找密集区域并将其分配给一个群集的能力。它的最大优点是它可以自行确定数据中的类数。我们将从dbscan模型创建3个功能：

类的数量（这里的假设是，类的数量过多将表明图像中的发票数量众多）。
噪声像素的数量。
模型中的轮廓分数（轮廓分数衡量每个像素的分类程度，我们将取所有像素的平均轮廓分数）

from sklearn.cluster import DBSCANfrom sklearn import metricsthr, imgage = cv2.threshold(gray_reduced_image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)img_df = pd.DataFrame(img).unstack().reset_index().rename(columns={'level_0': 'y', 'level_1': 'x'})img_df = img_df[img_df[0] == 0]X = image_df[['y', 'x']]db = DBSCAN(eps=1, min_samples=5).fit(X)# plt.scatter(image_df['y'], image_df['x'], c=db.labels_, s=3)# plt.show(block=False)core_samples_mask = np.zeros_like(db.labels_, dtype=bool)core_samples_mask[db.core_sample_indices_] = Truelabels = db.labels_# Number of clusters in labels, ignoring noise if present.n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)n_noise_ = list(labels).count(-1)image_df['class'] = labels# print('Estimated number of clusters: %d' % n_clusters_)# print('Estimated number of noise points: %d' % n_noise_)# print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(image_df, labels))features = pd.Series([n_clusters_, n_noise_, metrics.silhouette_score(image_df, labels)])

五、计算零点交叉

我们（灰度）图像中的每个像素的值都在0到255之间（在我们的示例中，零被视为白色，而255被视为黑色）。如果要计算“零”交叉，则需要对图像进行阈值处理—即设置一个值，以使较高的值将分类为255（黑色），而较低的值将分类为0（白色）。在我们的案例中，我使用了Otsu阈值。在执行图像阈值处理之后，我们将获得零和一作为像素，我们可以将其视为数据帧并将每一列和每一行相加：

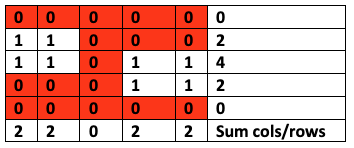
现在，假设1代表文本区域（黑色像素），0代表空白区域（白色像素）。现在，我们可以计算每行/列总和从任何正数变为零的次数。

img = img / 255df = pd.DataFrame(img)pixels_sum_dim1 = (1 - img_df).sum()pixels_sum_dim2 = (1 - img_df).T.sum()zero_corssings1 = pixels_sum_dim1[pixels_sum_dim1 == 0].reset_index()['index'].rolling(2).apply(np.diff).dropna()zero_corssings1 = zero_corssings1[zero_corssings1 != 1]num_zero1 = zero_corssings1.shape[0]zero_corssings2 = pixels_sum_dim2[pixels_sum_dim2 == 0].reset_index()['index'].rolling(2).apply(np.diff).dropna()zero_corssings2 = zero_corssings2[zero_corssings2 != 1]num_zero2 = zero_corssings2.shape[0]features = pd.Series([num_zero1, num_zero2])

六、归一化图像直方图

如果我们将图像视为信号，则可以使用信号处理工具箱中的一些工具。我们将使用重新采样的想法来创建更多功能。

怎么做？首先，我们需要将图像从矩阵转换为一维向量。其次，由于每个图像都有不同的形状，因此我们需要为所有图像设置一个重采样大小-在本例中。

使用插值，我们可以将信号表示为一个连续函数，然后我们将对其进行重新采样，采样之间的间隔为

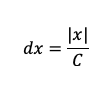
其中x表示图像信号，C表示要重采样的点数。

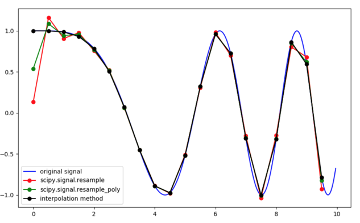
from scipy.signal import resampledim1_normalized_hist = pd.Series(resample(df.sum(), 16))dim2_normalized_hist = pd.Series(resample(df.T.sum(), 16))print(dim1_normalized_hist)print(dim2_normalized_hist)

七、DCT-离散余弦变换

离散余弦变换（DCT）用在不同频率振荡的余弦函数之和表示数据点的有限序列。DCT与DFT（离散傅立叶变换）不同，只有实部。DCT，尤其是DCT-II，通常用于信号和图像处理，尤其是用于有损压缩，因为它具有强大的“能量压缩”特性。在典型的应用中，大多数信号信息倾向于集中在DCT的几个低频分量中。我们可以在图像和转置图像上计算DCT向量，并取前k个元素。

from scipy.fftpack import dctdim1_dct = pd.Series(dct(df.sum())[0:8]).to_frame().Tdim2_dct = pd.Series(dct(df.T.sum())[0:8]).to_frame().T
dim1_normalize_dct = pd.Series(normalize(dim1_dct)[0].tolist())dim2_normalize_dct = pd.Series(normalize(dim2_dct)[0].tolist())
print(dim1_normalize_dct)print(dim2_normalize_dct)

八、结论

如今，CNN的使用正在增长，在本文中，我们试图解释和演示一些以老式方式从图像创建特征的经典方法，了解图像处理的基础是一种很好的做法，因为有时它更容易比将其推入网中更准确。本文是对图像的处理以及如何使用像素并从像素中提取知识的介绍，也许是对大脑的刺激。

END

整理不易，点赞三连↓