蔚来一面:HashMap 的 hash 方法原理是什么?
Warning:这是《Java 程序员进阶之路》专栏的第 55 篇。那天,小二去蔚来面试,面试官老王一上来就问他:HashMap 的 hash 方法的原理是什么?当时就把裸面的小二给蚌埠住了。
回来后小二找到了我,于是我就写下了这篇文章丢给他,并严厉地告诉他:再搞不懂就别来找我。听到这句话,心头一阵酸,小二绷不住差点要哭 😭。
PS:本文 GitHub 上已同步,有 GitHub 账号的小伙伴,记得看完后给二哥安排一波 star 呀!冲一波 GitHub 的 trending 榜单,求求各位了。
GitHub 地址:https://github.com/itwanger/toBeBetterJavaer
在线阅读地址:https://itwanger.gitee.io/tobebetterjavaer
来看一下 hash 方法的源码(JDK 8 中的 HashMap):
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
这段代码究竟是用来干嘛的呢?
我们都知道,key.hashCode() 是用来获取键位的哈希值的,理论上,哈希值是一个 int 类型,范围从-2147483648 到 2147483648。前后加起来大概 40 亿的映射空间,只要哈希值映射得比较均匀松散,一般是不会出现哈希碰撞的。
但问题是一个 40 亿长度的数组,内存是放不下的。HashMap 扩容之前的数组初始大小只有 16,所以这个哈希值是不能直接拿来用的,用之前要和数组的长度做取模运算,用得到的余数来访问数组下标才行。
取模运算有两处。
取模运算(“Modulo Operation”)和取余运算(“Remainder Operation ”)两个概念有重叠的部分但又不完全一致。主要的区别在于对负整数进行除法运算时操作不同。取模主要是用于计算机术语中,取余则更多是数学概念。
一处是往 HashMap 中 put 的时候(putVal 方法中):
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
HashMap.Node<K,V>[] tab; HashMap.Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
}
一处是从 HashMap 中 get 的时候(getNode 方法中):
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {}
}
其中的 (n - 1) & hash 正是取模运算,就是把哈希值和(数组长度-1)做了一个“与”运算。
可能大家在疑惑:取模运算难道不该用 % 吗?为什么要用 & 呢?
这是因为 & 运算比 % 更加高效,并且当 b 为 2 的 n 次方时,存在下面这样一个公式。
a % b = a & (b-1)
用 替换下 b 就是:
a % = a & ( -1)
我们来验证一下,假如 a = 14,b = 8,也就是 ,n=3。
14%8,14 的二进制为 1110,8 的二进制 1000,8-1 = 7 的二进制为 0111,1110&0111=0110,也就是 0*
+1*
+1*
+0*
=0+2+4+0=6,14%8 刚好也等于 6。
这也正好解释了为什么 HashMap 的数组长度要取 2 的整次方。
因为(数组长度-1)正好相当于一个“低位掩码”——这个掩码的低位最好全是 1,这样 & 操作才有意义,否则结果就肯定是 0,那么 & 操作就没有意义了。
a&b 操作的结果是:a、b 中对应位同时为 1,则对应结果位为 1,否则为 0
2 的整次幂刚好是偶数,偶数-1 是奇数,奇数的二进制最后一位是 1,保证了 hash &(length-1) 的最后一位可能为 0,也可能为 1(这取决于 h 的值),即 & 运算后的结果可能为偶数,也可能为奇数,这样便可以保证哈希值的均匀性。
& 操作的结果就是将哈希值的高位全部归零,只保留低位值,用来做数组下标访问。
假设某哈希值为 10100101 11000100 00100101,用它来做取模运算,我们来看一下结果。HashMap 的初始长度为 16(内部是数组),16-1=15,二进制是 00000000 00000000 00001111(高位用 0 来补齐):
10100101 11000100 00100101
& 00000000 00000000 00001111
----------------------------------
00000000 00000000 00000101
因为 15 的高位全部是 0,所以 & 运算后的高位结果肯定是 0,只剩下 4 个低位 0101,也就是十进制的 5,也就是将哈希值为 10100101 11000100 00100101 的键放在数组的第 5 位。
明白了取模运算后,我们再来看 put 方法的源码:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
以及 get 方法的源码:
public V get(Object key) {
HashMap.Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
它们在调用 putVal 和 getNode 之前,都会先调用 hash 方法:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
那为什么取模运算之前要调用 hash 方法呢?
看下面这个图。
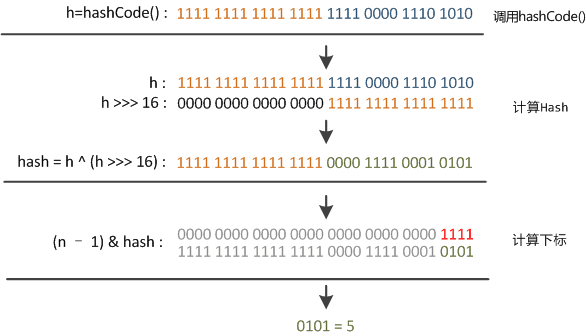
某哈希值为 11111111 11111111 11110000 1110 1010,将它右移 16 位(h >>> 16),刚好是 00000000 00000000 11111111 11111111,再进行异或操作(h ^ (h >>> 16)),结果是 11111111 11111111 00001111 00010101
异或(
^)运算是基于二进制的位运算,采用符号 XOR 或者^来表示,运算规则是:如果是同值取 0、异值取 1
由于混合了原来哈希值的高位和低位,所以低位的随机性加大了(掺杂了部分高位的特征,高位的信息也得到了保留)。
结果再与数组长度-1(00000000 00000000 00000000 00001111)做取模运算,得到的下标就是 00000000 00000000 00000000 00000101,也就是 5。
还记得之前我们假设的某哈希值 10100101 11000100 00100101 吗?在没有调用 hash 方法之前,与 15 做取模运算后的结果也是 5,我们不妨来看看调用 hash 之后的取模运算结果是多少。
某哈希值 00000000 10100101 11000100 00100101(补齐 32 位),将它右移 16 位(h >>> 16),刚好是 00000000 00000000 00000000 10100101,再进行异或操作(h ^ (h >>> 16)),结果是 00000000 10100101 00111011 10000000
结果再与数组长度-1(00000000 00000000 00000000 00001111)做取模运算,得到的下标就是 00000000 00000000 00000000 00000000,也就是 0。
综上所述,hash 方法是用来做哈希值优化的,把哈希值右移 16 位,也就正好是自己长度的一半,之后与原哈希值做异或运算,这样就混合了原哈希值中的高位和低位,增大了随机性。
说白了,hash 方法就是为了增加随机性,让数据元素更加均衡的分布,减少碰撞。
参考链接:
https://blog.csdn.net/lonyw/article/details/80519652 >https://zhuanlan.zhihu.com/p/91636401 >https://www.zhihu.com/question/20733617
点击下方的名片,回复关键字「03」 就可以获取《Java 程序员进阶之路》的 PDF 版了。
点击阅读原文也可以跳转到在线阅读地址,我们下期见(记得给二哥 star 哦)~