2020 年美国大选：一个生动的统计学课堂-轻识

↑↑↑点击上方蓝字，回复资料，10个G的惊喜

作者：杨笛笛

主页：https://www.zhihu.com/people/yang-di-di-62/posts

2016年美国大选，民调机构的预测滑铁卢了
今年大选，民调机构几乎是再次吃瘪，为什么民调数据总会出现偏差呢？
杨笛笛老师这篇文章生动地回答了这个问题

文末赠书福利

先给还没学过统计学的同学再简单讲一讲抽样这个概念。

抽样一般分三步：

1.定义好你想描述的总体。

2. 明确你到底要测量什么。

3. 决定用什么方法从总体中选出样本。

比如说我家在上海开了一家川菜餐厅，我想调研一下现在的口味被不被上海顾客接受。

那么在这个例子里：

我想描述的总体是所有上海顾客。
我要测量的是他们接不接受现在的辣度。
最后得到一个yes or no的答案。
我决定在顾客用餐的时候安排服务员逐一发放问卷。

好了最终我发现10份问卷里面，接受现在辣度的客人达到了9个。于是我得出一个结论：“我们餐厅的口味被上海人接受。”

我这个结论会有什么样的问题？

一共只有10份问卷导致方差（variance）或者说随机性太大。
有可能是服务员运气好刚好找到的都是喜欢辣味的顾客。
如果同样的抽样再做一次，说不定就只有5个人喜欢吃辣了。
就好像你扔一个公平硬币（正面概率0.5）10次，有时候3个正面有时候6个正面，这就是随机性。
那这个问题怎么解决呢？
最粗暴的方法就是增加样本量（sample size），扔10次硬币能得到4-6个正面概率只有65%左右，而扔1000次硬币得到400-600个正面的概率就几乎100%了。
除了增加样本量，还有一些其他的方法降低随机性，比如采用分层抽样等更高级的抽样手段。

2. 在现在这个例子中，总体是所有的上海顾客，样本呢？可以代表所有上海客人吗？不是的，我的样本是“那些愿意来这家新开的餐厅吃饭的上海客人”。这家餐厅开在一家商场的最高层，如果不是想好了要找来的话，很难有人闲逛进店吃饭。因此样本和总体的差异导致了我的结论不准确，因为那些愿意来川菜餐厅吃饭的客人显然平均上是比一个普通上海人更能接受辣味的。换句话说，我的样本不够有“代表性”（representative）。这个总体和样本在本质上的差异，在统计学上叫作偏差（Bias）。

用下面这个图再给大家解释一下方差和偏差的区别。

左上角是低方差低偏差，所有的飞镖都扔中了中间那一环。这时候你瞄对了地方，并且随机性很低。在数据上就是样本随机性小，并且很有代表性。

右上角是高方差低偏差，飞镖散落在了红心周围。这时候表示你瞄准的地方是对的，但是随机性太大了。在数据上就是样本有代表性，但是随机性很高。

左下角是低方差高偏差，飞镖都落在了距离红心一段距离的地方。这时候是你瞄准的地方错了，虽然随机性很低。在数据上就是样本随机性低，但是没有代表性。

右下角是高方差高偏差，说明你既没瞄准，还不会扔。数据上就是随机性又高，还没有代表性。

其实所有的调研都会面临这两个问题：

一是随机性，也就是方差。

二是样本和总体有本质性的区别，也叫作偏差。

在调研里，方差的问题很好解决，钱给够，扩大样本就行。

而偏差的问题往往会复杂很多，需要更细致的抽样设计来尽量避免。

说起偏差这个话题，前年的高考作文中出现的“幸存者偏差”其实就是个很有趣的故事。

二战期间，盟军想要给战斗机加一些装甲增加防御性。但是当时物资有限，他们无法给整架飞机都加上装甲。因此军方的专家就需要研究出飞机上的哪些部位是最脆弱的并给这些部位加上装甲。

为了做出推断，军方专家从那些受伤了并飞回来的飞机中采集数据进行分析。他们最终发现这些飞机上的引擎和机舱都没有中弹（如下图所示）。自然而然地专家们得出结论“应该给给机翼和机身还有机尾增加装甲，驾驶舱和引擎不用管，这两个地方不会中弹。”

这时候有一位叫Abraham Wald的数学家指出了他们推断中的漏洞：军方专家只分析了这些成功飞回基地的飞机。这些飞机之所以能飞回基地，是因为机身机翼中弹并没有对飞机造成致命伤害，不然它们早就被打下去了。他建议给引擎和机舱加装甲，因为并不是说德军的防空炮刻意打机身机翼而漏掉机舱和引擎（那个时候的防空炮扫射基本上就是看运气，不可能说精确地瞄准某个部位），之所以飞回来的飞机这些部位没中弹，是因为这些部位中弹的飞机都没飞回来！

通过分析那些被击落的飞机，Wald孕育出了“幸存者偏差”这个概念。二战时期还有很多统计学概念被提出运用，并且大多得到了比军方智库更好的效果，感兴趣的可以看一下“德军坦克问题”(The German Tank Problem)。

刚才这个故事里，盟军想研究的总体是所有盟军的飞机，而样本是那些可以飞回来的飞机。这些飞回来的飞机显然不具有足够的代表性。那么如果用这些样本来对总体做推断，就会出现偏差。

还有个常见的例子就是那些宣传读书无用论的人。“啊你看看比尔盖茨，乔布斯，扎克伯格他们都没有大学毕业，现在全是亿万富翁。” 这里我们关心的总体是所有高中没毕业的人，而样本是“高中没毕业并且很出名人人都知道的人。”你怎么不想想那些被忽略掉的成千上万的其他辍学的人过得怎么样了？用这样有严重偏差的样本去对总体做推断的人，不是蠢就是坏。

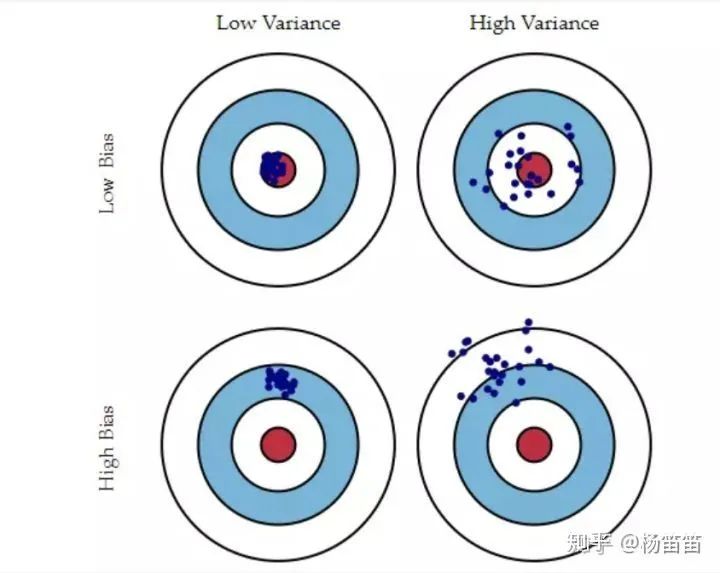
其他的偏差主要来源还有：

覆盖面不全偏差(Undercoverage bias)：发生在当总体中的一部分子集被忽略掉的时候。比如2008年美国大选的调研通过的是电话座机，但是当时很多年轻人已经不用座机只用手机了，那这部分年轻人就被忽略掉了从而产生了undercoverage bias. 再比如某电视节目在结束之后发出问卷，问观众们对节目满意吗？接着得出了95%满意的样本数据。问题是那些不满意的人早就换台了...还能被你采样吗？在这次大选民调里举个例子也许就是一个调研人员跑到BLM的集会去问:"你支持拜登吗？" 那些红脖子们就在这里被忽略掉了，这就会产生undercoverage bias.

无应答偏差（Nonresponse bias）：发生在当总体的某些子集无法被联系上，或者是拒绝回答问题时。在国外居住过的人肯定经常在邮箱里发现调研公司或者广告公司寄来的纸质版调研，而大部分人都会选择拆都不拆直接扔垃圾箱。纸质信件调研可能是最容易发生无应答偏差的调研方法，实际上研究人员根本就不知道是哪部分总体的子集在回他们的信，也就不知道这些样本又可以代表什么。

应答偏差（Response bias）：调研的问题本身可能就会导致误导性结果，或者说回答问题的人刻意歪曲一些事实。比如电视观众肯定不好意思承认自己喜欢看某些栏目或者某些类型的电影，女生倾向把自己的体重写得偏低，男生会把自己的收入写得偏高。之前我在学期中给所有班级发了一次匿名问卷，其中有两个问题是“你觉得考试难度如何？” 还有 “你觉得作业量如何？” 几乎所有人都和我说考试太难了，作业太多了，你们觉得我会信吗？学期刚开始的时候我利用同学们对我的畏惧，做了一次关于我颜值的现场不匿名调研，结果发现我颜值满分，你觉得我能信吗，我难道能以此为据开始靠脸吃饭不靠才华了？结合大选，就像一个调研人员打电话给一个红脖子问：：你选拜登吗？” 红脖子怎么说？是直接和调研人员开骂？还是说“yes yes sure sure"应付了事？（顺便还能误导敌方）

措辞偏差（Wording bias）：可能是最重要的影响调研结果的因素了。非中性或者措辞糟糕的问题可以得到对总体非常缺乏代表性的样本。假如说民主党的调研人员如果打电话给中立选民问："作为上帝虔诚的子民，为了让我们的国家摆脱疫情重振经济，难道你不选我们备受尊敬的拜登先生吗?" 你觉得人家要怎么回答？

自愿应答偏差(Voluntary response bias) ：当回答是非强制时会发生的偏差。最常见的例子是电视节目里接听观众来电，国外的那种访谈节目里很多观众电话一通就开始骂（不管是骂谁）。这是因为，如果我对话题毫不在乎的话，我会打电话给你说"I don't really care”吗？因此这些自愿费时费力打电话参加节目的观众必然都是情绪激动，观点偏激的那部分，而大多数观众很可能和我一样完全就不感兴趣。那么如果在网络舆论都支持拜登的情况下，哪个红脖子会在电视上或者网上发表对川普有利的评论？要是哪个红脖子发一句"川普必胜"，那估计评论区的脏话得把他淹没了，何必自讨没趣呢？

那么同学们，这次大选民调里有可能出现哪些问题？美国的专业民调公司是不会缺钱的，样本不会不够，随机性是可控的。那么在哪里又会出现偏差呢？

我感觉以上提到的每一种偏差都会在民调里体现，并且还有一种最终极的偏差来源，那就是：

那些要投川普的人假装自己要投给拜登，以此来误导民调。

这怎么办？完全无解啊。

我怎么想的凭什么告诉你？

而且你还没办法把这些人给筛选出来，人家就是装得和拜登支持者一模一样。

最后再次强调用假设检验和置信区间写结论的时候一定要用non-deterministic language模糊性用语。

千万不要把话说满了："拜登赢定了"。

要说：

"我们在α=5%的情况下，有足够的证据拒绝掉特朗普有更多支持者的原假设。”

最后结论翻车打脸了也和我没关系，是证据说的结论，不是我说的，证据错了怪我咯？我也是受害者啊！

用置信区间来说也是这样。