什么时候可以用双指针,该咋用?
什么情况可以用双指针,该咋用?
双指针是我们做题中经常用到的思想,所以这个思想在刷题初期是一定要会的。其实我们早就学习过这个方法,那就是我们在学习数据结构的二分查找,下面我们通过二分查找来描述一下这个思想。
二分查找首先定义两个指针,左指针和右指针,分别指向数组的头和尾,然后计算出他俩的中间的索引,其值和目标值进行比较,如果目标值更大则说明目标值在中间索引和右指针中间,则需要移动左指针到中间索引的后一位。如果目标值比中间值小,则需要移动右指针到中间索引的前一位。不断执行,直至找到目标值,若该数组不含有目标值,则左指针和右指针重合时跳出该循环。
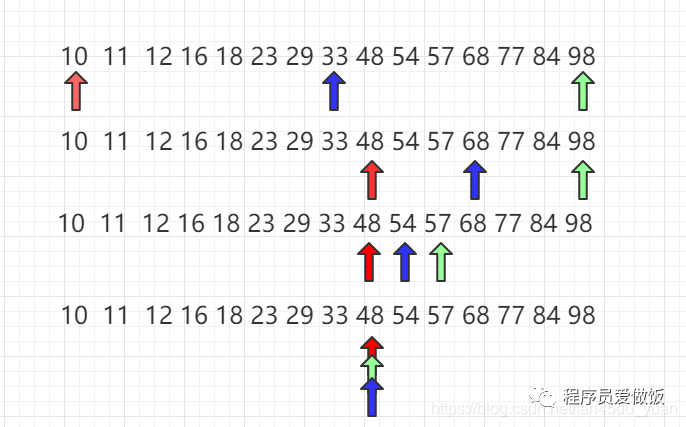
二分查找代码
public static int halfnum(int[] arraynum ,int b){
int hi =arraynum.length-1;
int lo = 0;
//先判断数组是不是空
if (arraynum.length==0){
return -1;
}
while(hi>=lo){
//判断是否等于要猜的数,中间值
if(b==arraynum[(hi+lo)/2]){
return (hi+lo)/2;
}
//大于中间数的情况
else if (b>arraynum[(hi+lo)/2]){
lo= (hi+lo)/2+1;
}
//小于中间数的情况
else{
hi=(hi+lo)/2-1;
}
}
return -1;
}
35.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
题目很好理解,但是我们想要一次AC是不太容易的。我们根据题意可以想到,这样共有四种可能
插入情况无非就这几种
(1)比数组里的任何值都小,插入头部
(2)比数组里的任何值都大,插入尾部
(3)查询到数组元素,返回该处索引值
(4)数组内无该元素,将其插入两元素之间。
所以我们可以通过以下代码实现该题
class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
//中间值,与target对比
int mid = (left + right) / 2;
//第三种情况
if(nums[mid] == target) {
return mid;
//移动左指针
} else if(nums[mid] < target) {
left = mid + 1;
} else {
//移动右指针
right = mid - 1;
}
}
//1,2,4三种情况都在循环内部,我们只需输出左指针即可。
return left;
}
}
刚才我们说了双指针思想的重要性,下面这个题目也是可以完全通过双指针思想实现的,所以说双指针的思想是必须有的。你可以通过下面这个题目完全体会到双指针的重要性
27.移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
给定 nums = [3,2,2,3], val = 3,函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,1,2,2,3,0,4,2], val = 2,函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
注意这五个元素可为任意顺序。
你不需要考虑数组中超出新长度后面的元素。
该题目我们可以创建两个指针,一前一后,前面的负责探路后面的负责填充,当前面查询到需要移除的元素时直接跳过该元素,继续前进。后面的指针只负责往该数组里面填充不需要移除的数字。所以我们可以根据以下代码实现
class Solution {
public int removeElement(int[] nums, int val) {
//特殊情况
if(nums==null){
return 0;
}
int j = 0;//慢指针,i代表快指针
for(int i = 0;i //正常情况直接赋值给i
if(nums[i]!=val){
nums[j]=nums[i];
j++;
}
//如果为需要删除的值时,则快指针移动,慢指针不动。
}
return j;
}
}
刚才我们学习了两个双指针的题目,是不是对这个做题思想有了一些理解了,下面我们来使用一个更加高级的双指针,这个也是经常使用的思想,但是归根结底还是双指针思想。
该题目的思想也是双指针的思想,不过这个代码比较难写一些,用到的情况也是比较多的,所以我们这个题目要用心体会一下。
209,长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组
题目含义比较好理解,则是在数组里面找出长度最小的子数组,子数组的元素和大于等于目标值。这个题目我们就用到了滑动窗口的思想。
滑动窗口:就是通过不断调节子数组的起始位置和终止位置,进而得到我们想要的结果我们也可以看成是双指针的一种。
在该题中,我们可能遇到这种情况 大家思考一下,数组的值是1,2,3,4,5我们的s为5,所以我们第一次的子数组(滑动窗口)长度则为3,1+2+3>5,这时左指针在1的位置,右指针在3的位置,但是2+3=5同样符合,所以我们就需要移动左指针,此时窗口长度则改为2了。然后我们保留该值,继续移动左指针,判断3是否仍符合,此时发现不符合了,则需要移动右指针,移动到下一个符合情况的元素,继续执行刚才的步骤,直到数组的最后。所以整个过程中滑动窗口的长度变化为,3,2,3,2,3,2,1,最小的则为1.
我们可以通过以下代码解决该题。
class Solution {
public int minSubArrayLen(int s, int[] nums) {
int chiledlen = Integer.MAX_VALUE;
int winlen = 0;//窗口大小
int sum = 0;
int i = 0;//起始长度位置
for(int j = 0 ; j < nums.length;j++){
sum += nums[j];
//发现符合条件的情况
//循环内部的代码是精髓所在
while(sum>=s){
winlen = j-i+1;
chiledlen = Math.min(chiledlen,winlen);
//下面两行是滑动窗口的意义所在,改变起点位置,判断是否仍符合条件
sum-=nums[i];
i++;
}
}
return chiledlen == Integer.MAX_VALUE ? 0:chiledlen;
}
}
通过以上三个题目我们是不是对双指针思想有了一些理解了,该思想不仅可以用在数组的题目上,链表同样适用。所以我们要完全掌握,如果觉得题目还不错的话,可以推荐给需要的人。
来个直击灵魂的三连吧!
