通俗理解贝叶斯优化
选自Medium
作者:Andre Ye
机器之心编译
编辑:Panda
贝叶斯优化是机器学习超参数优化的常用技术之一,本文不会使用艰深的数学论证,而是通过简单的术语带你领略贝叶斯优化之美。
计算成本高。理想情况下,只要我们查询函数的次数足够多,我们就能在实质上将它复现出来,但在实际情况下,输入的采样很有限,优化方法必须在这种情况下也能有效工作。
导数未知。在深度学习以及其它一些机器学习算法中,梯度下降及其变体方法依然是最常用的方法,这当然是有原因的。知道了导数,能让优化器获得一定的方向感——我们没有这种方向感。
我们需要找到全局最小值,这个任务即使对于梯度下降这种复杂精细的方法来说也很困难。我们的模型有时需要某种机制来避免被困于局部最小值。

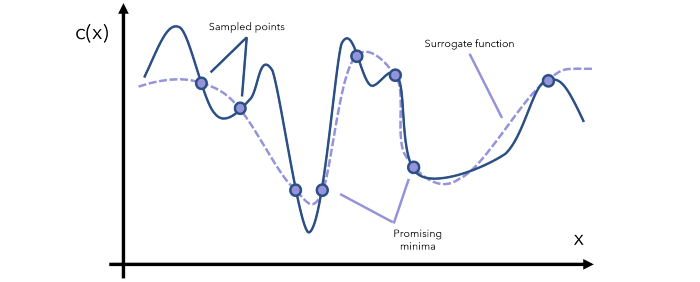

利用的目标是采样代理模型能很好地预测目标函数的地方。这会用到已知的有潜力的位置。但是,如果我们已经充分探索了某个特定的区域,再继续利用已知信息也收益不大了。
探索的目标是采样不确定度较高的位置。这能确保空间中不留下未探索的主要区域——全局最小值可能就藏在此处。
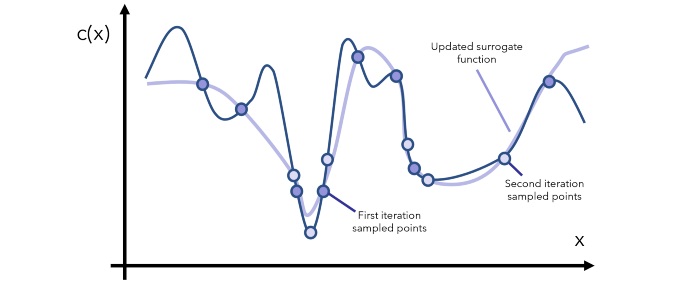
初始化一个高斯过程「代理函数」先验分布。
选择几个数据点 x 使得获取函数 a(x) 在当前先验分布上的结果是最大的。
在目标成本函数 c(x) 中评估数据点 x 并获取其结果 y。
使用新数据更新高斯过程先验分布,得到一个后验分布(这将作为下一步的先验分布)。
重复第 2-5 步并多次迭代。
解读当前的高斯过程分布(成本很低),找到全局最小值。
代理优化是使用一个代理函数或近似函数来通过采样估计目标函数。
贝叶斯优化是通过将代理函数表示成概率分布而将代理优化放入一个概率框架中,然后再使用新信息更新这个分布。
获取函数则是用于基于已知的先验,评估利用空间中的某个特定点得到「好」结果的概率。其关键在于探索与利用的平衡。
贝叶斯优化的主要使用场景是目标函数评估成本高的任务,比如超参数调节。有一些用于该任务的软件库,比如 HyperOpt。
往期精彩:

