黎曼猜想和哥德巴赫猜想有什么联系?
数学算法俱乐部
日期 : 2020年12月28日
正文共 :5347字
作者 : 郁林成森严格上讲黎曼猜想与哥德巴赫猜想并没有特别明显的联系(至少现在应该没有什么神奇的定理表明二者是等价的),不过在对哥德巴赫猜想的研究过程中黎曼猜想确实扮演了类似敲门砖的作用。先讲黎曼猜想(the Riemann Hypothesis):
一、黎曼![]() 函数
函数
所谓的黎曼
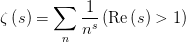 在
在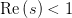 这大半个复平面上的解析延拓(analytic continuation).因为在
这大半个复平面上的解析延拓(analytic continuation).因为在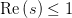 这里上述级数是不收敛的,1859年德国数学家伯恩哈德·黎曼(Bernhard Riemann)于1859年在其文《论小于给定数值的素数个数》中首先找到了如下的解析延拓
这里上述级数是不收敛的,1859年德国数学家伯恩哈德·黎曼(Bernhard Riemann)于1859年在其文《论小于给定数值的素数个数》中首先找到了如下的解析延拓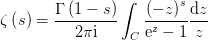 可以证明,在上述解析延拓中除了在
可以证明,在上述解析延拓中除了在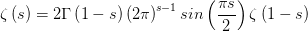 首先可以从上述表达式中看出黎曼
首先可以从上述表达式中看出黎曼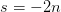 (
(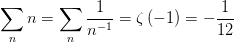 这毕竟是很多民科“引以为豪”的结果).黎曼发现
这毕竟是很多民科“引以为豪”的结果).黎曼发现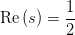 的直线上学界称这条直线为临界线(critical line)我们可以很容易地从上面函数方程中看出来黎曼
的直线上学界称这条直线为临界线(critical line)我们可以很容易地从上面函数方程中看出来黎曼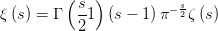 容易发现
容易发现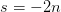 是
是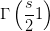 极点,所以也就不是
极点,所以也就不是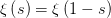 这下子对称性就变得尤为明显了。我们记
这下子对称性就变得尤为明显了。我们记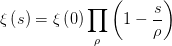 这里
这里猜想一:在
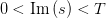 的区域内,
的区域内,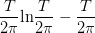 猜想二:在
猜想二:在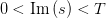 的区域内,
的区域内,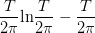 猜想三:
猜想三:二、黎曼![]() 函数与素数分布
函数与素数分布
熟悉初等数论的人都知道欧拉(L.Euler)在1737年发表的一个著名公式
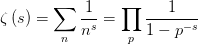 其中
其中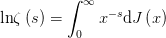 这里
这里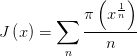 ,其中
,其中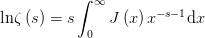 这下子联系就比较露骨了,左边是万能的
这下子联系就比较露骨了,左边是万能的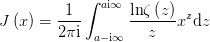 而利用简单的莫比乌斯反演(Mobius inversion)可以得到
而利用简单的莫比乌斯反演(Mobius inversion)可以得到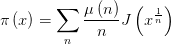 这样我们就把素数分布函数
这样我们就把素数分布函数三、素数定理
对素数规律的探求一直是数论领域的核心问题。对于
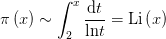 独立于高斯,勒让德(Legendre)也有如下猜测:
独立于高斯,勒让德(Legendre)也有如下猜测: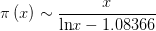 容易看出,这两者是等价的(不过我一直好奇1.08366是怎么找出来的……),共同被称为素数定理. 1896年,阿达马与普桑(de la Valee Poussin,这名一看就是上流社会)分别独立证明了黎曼
容易看出,这两者是等价的(不过我一直好奇1.08366是怎么找出来的……),共同被称为素数定理. 1896年,阿达马与普桑(de la Valee Poussin,这名一看就是上流社会)分别独立证明了黎曼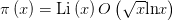 反之,从这个公式也可以推出黎曼假设是对的,也就是说两者是等价的。(黎曼假设还有一个很有意思的等价命题:对所有的
反之,从这个公式也可以推出黎曼假设是对的,也就是说两者是等价的。(黎曼假设还有一个很有意思的等价命题:对所有的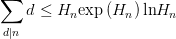 其中
其中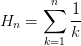 ,等价性由Jeff Lagarias证明)
,等价性由Jeff Lagarias证明)四、广义黎曼假设(GRH)
即使研究黎曼猜想受阻,但依然拦不住数学家们想要高飞的心。所谓的广义黎曼猜想,就是黎曼猜想的2.0版本,不过其研究对象由黎曼
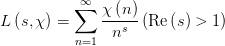 在
在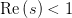 上的解析延拓,其中
上的解析延拓,其中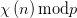 是狄利克雷特征,称此函数为模
是狄利克雷特征,称此函数为模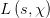 的非平凡零点都位于临界线上显然,这个比黎曼猜想牛b多了,当然也难证多了。现代数论研究中,多以GRH为假设进行讨论,与黎曼假设类似,GRH可以推出:当
的非平凡零点都位于临界线上显然,这个比黎曼猜想牛b多了,当然也难证多了。现代数论研究中,多以GRH为假设进行讨论,与黎曼假设类似,GRH可以推出:当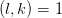 ,令算术序列
,令算术序列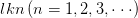 中不超过
中不超过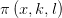 ,则有
,则有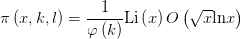 同样的,这个公式反过来也能推出GRH.
同样的,这个公式反过来也能推出GRH.五、研究进展
基本离证明还差得远呢……(好吧好吧,我承认是来凑字数的) 不过有好多有希望的想法,有复变函数论的(黎曼猜想多半是个复变函数问题),有解析数论的,有非对易几何的(代表人物法国大数学家孔涅,不过希望渺茫)还有量子力学的!!!(没错,确实有量子力学的,参见“希尔伯特—波利亚猜想”)但怎么有种有生之年看不到的感觉……
简单介绍一下孔涅的研究:(严格上说孔涅的证明思路是属于量子力学的,但他在研究过程中确实也用了非对易几何,具体效果如何恐怕不容乐观。)孔涅写出了一组方程,用其构造了一个量子力学体系,这个体系的本征值恰好对应着黎曼ζ函数在临界线上的非平凡零点,如果孔涅能证明出了对应本征值的零点外没有其他非平凡零点了,那也就相当于证明了黎曼猜想了,但就目前来看要做到这一点难比登天。
六、哥德巴赫猜想(Goldbach Problem)
在1742年给欧拉的一封信中,哥德巴赫提出了两个猜想,欧拉用稍微简练的语言改下后表述如下:(哥德巴赫猜想)每一偶数
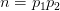 . (弱哥德巴赫猜想)每一奇数
. (弱哥德巴赫猜想)每一奇数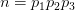 . 很明显,哥德巴赫猜想可以推出弱哥德巴赫猜想。在1900年的第二届国际数学家大会上,大卫·希尔伯特(D.Hilbert)向全世界的数学家们建议了23个问题,其中哥德巴赫猜想便是第八问题的一部分。12年后的第五届国际数学家大会上,兰道又将其作为素数论中未解决的4个难题加以推荐,时至今日,对哥德巴赫猜想的研究极大带动了解析数论的发展,从这个意义上来讲,哥德巴赫猜想可谓是素数论中的核心问题。
. 很明显,哥德巴赫猜想可以推出弱哥德巴赫猜想。在1900年的第二届国际数学家大会上,大卫·希尔伯特(D.Hilbert)向全世界的数学家们建议了23个问题,其中哥德巴赫猜想便是第八问题的一部分。12年后的第五届国际数学家大会上,兰道又将其作为素数论中未解决的4个难题加以推荐,时至今日,对哥德巴赫猜想的研究极大带动了解析数论的发展,从这个意义上来讲,哥德巴赫猜想可谓是素数论中的核心问题。七、弱哥德巴赫猜想与GRH
数学家们首先向弱哥德巴赫猜想发起冲锋。第一次重大突破发生在20年代,哈代(Hardy)和李特尔伍德(Littlewood)在其“算术分拆”的系列文章中创立并发展了“圆法”即把方程
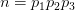 的解数表为积分,并将积分区间
的解数表为积分,并将积分区间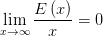 .这一方面表明在GRH的假定下,哥德巴赫猜想基本成立;另一方面有暗示广义黎曼假设与公理体系中的很多定理是相容的,这就增强了GRH的可信度。 直接来说,在哈代和李特尔伍德的证明中用到了GRH导出的有关
.这一方面表明在GRH的假定下,哥德巴赫猜想基本成立;另一方面有暗示广义黎曼假设与公理体系中的很多定理是相容的,这就增强了GRH的可信度。 直接来说,在哈代和李特尔伍德的证明中用到了GRH导出的有关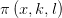 的估计式:对任意的
的估计式:对任意的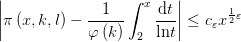 这明显是GRH的算术形式,用素数定理的方法来处理优弧上的积分当然也可以但是不足以推出弱哥德巴赫猜想。 到1936年事情出现了转机,帕奇(A.Page)与西格尔(C.L.Siegel)分别先后独立证明有关
这明显是GRH的算术形式,用素数定理的方法来处理优弧上的积分当然也可以但是不足以推出弱哥德巴赫猜想。 到1936年事情出现了转机,帕奇(A.Page)与西格尔(C.L.Siegel)分别先后独立证明有关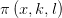 的估计式,他们的结果虽然比GRH要弱很多但是已经比当时已取得的结果要强不少,也足以导出优弧上的积分估计。数学家们意识到哈代和李特尔伍德证明中的GRH是有可能被取消的,稍后维诺格拉多夫(Vinogradov)和埃斯特曼证明了:每一个充分大的奇数
的估计式,他们的结果虽然比GRH要弱很多但是已经比当时已取得的结果要强不少,也足以导出优弧上的积分估计。数学家们意识到哈代和李特尔伍德证明中的GRH是有可能被取消的,稍后维诺格拉多夫(Vinogradov)和埃斯特曼证明了:每一个充分大的奇数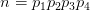 和每一个充分大的整数
和每一个充分大的整数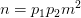 .大多数人认为在不依赖于GRH的传统圆法证明中这已经是很好的结果了,很难被超越了。1937年,维诺格拉多夫改造了传统圆法,将劣弧上的积分化为估计三角和
.大多数人认为在不依赖于GRH的传统圆法证明中这已经是很好的结果了,很难被超越了。1937年,维诺格拉多夫改造了传统圆法,将劣弧上的积分化为估计三角和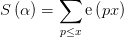 其中
其中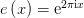 ,他给出了
,他给出了八、哥德巴赫猜想与GRH
对哥德巴赫猜想的研究主要是围绕圆法进行的,以华罗庚为代表的中国解析数论学派在其中发挥着举足轻重的作用。筛法源于公元前250年的Eralosthenes筛法,Eralosthenes用该方法制作出了世上第一张素数表。1919年,布伦对传统筛法进行了大幅度改进,并首先将其应用于哥德巴赫猜想的研究,他证明了 每一个充分大的偶数都是两个素因子个数不超过9的整数之和,简记为“9+9” 我们可以类似定义
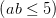 。时间相隔不远,在王元之前其同事潘承洞证明了1+5和1+4。1957年春,王元在假定GRH成立的情况下证明了1+3,在此之前的最好结果是埃斯特曼的在GRH下的1+6和王元、维诺格拉多夫在GRH下的1+4。剩下的事就都知道了……陈景润发表了惊天地泣鬼神的《大偶数表示一个素数及一个不超过2个素数之和》论文,达到了筛法的巅峰远超此前取得的所有结果,不用GRH证明了1+2。陈景润证明1+2后人们普遍认为由于筛法自身的局限性,很有可能1+2便是最好的结果(此前人们认为筛法最多到1+3),因此如果想在陈氏定理上更进一步甚至证明哥德巴赫猜想,就需要引进更加新颖而且强有力的技术。
。时间相隔不远,在王元之前其同事潘承洞证明了1+5和1+4。1957年春,王元在假定GRH成立的情况下证明了1+3,在此之前的最好结果是埃斯特曼的在GRH下的1+6和王元、维诺格拉多夫在GRH下的1+4。剩下的事就都知道了……陈景润发表了惊天地泣鬼神的《大偶数表示一个素数及一个不超过2个素数之和》论文,达到了筛法的巅峰远超此前取得的所有结果,不用GRH证明了1+2。陈景润证明1+2后人们普遍认为由于筛法自身的局限性,很有可能1+2便是最好的结果(此前人们认为筛法最多到1+3),因此如果想在陈氏定理上更进一步甚至证明哥德巴赫猜想,就需要引进更加新颖而且强有力的技术。九.黎曼猜想可能构成哥德巴赫猜想的证明吗?
我的感觉是不太可能,且容我缓缓道来…… 就目前在整个数学上的地位来讲(我从对数学的发展角度出发说一点不成熟的见解),哥德巴赫猜想肯定是无法与黎曼猜想匹敌。因为哥德巴赫猜想横竖就是个数论问题,再牛B也就是个数论问题,而且从目前来看它也并未对除堆垒数论以外的数论分支产生重大影响,在这一点上它连费马大定理(FLT)也比不过。而黎曼猜想则不同,其证明不但对数论领域有深刻影响,而且可以对复变函数论的发展起相当积极的推动作用(前面说过了,黎曼猜想多半是个复分析问题),也就是说黎曼猜想是数学界最重要的问题,而哥德巴赫猜想则更像是某个智力竞赛题。那么,到底黎曼猜想可能构成哥德巴赫猜想的某种证明吗?要回答这一问题,首先就要回顾一下哥德巴赫猜想的历史(翻前文):迄今为止,对哥德巴赫猜想的并未用到黎曼猜想,而是清一色用的是更厉害的广义黎曼猜想。原因很简单,黎曼猜想在这个问题上不够强!!另外,很有可能单从证明上讲黎曼猜想就要比哥德巴赫猜想难得多,更别提广义黎曼猜想。有可能若干年后,出了一位不世出的天才以不世出的方法证明了哥德巴赫猜想,但黎曼猜想仍然悬而未决。
最后说一句,哥德巴赫猜想跟孪生素数猜想有着极为深刻的联系,哥德巴赫猜想的相关结果一般而言是可以转换成孪生素数猜想的相关结果的,比如陈景润也曾证明过这样一个定理:存在无穷对素数
这跟他的1+2很像,也跟孪生素数猜想很接近。
— THE END —
 ☞曲面论
☞曲面论☞大学数学(高数线代)直观理解(一)☞读博期间强烈怀疑自己所在学科的价值是一种什么样的体验?☞罗杰·科恩伯格:基础科学——人类进步的希望☞太巧了!学霸夫妻携手进入武大读博,两人的硕士导师也是一对夫妻☞21岁MIT本科生推动数学重要问题新进展,曾获阿里数学竞赛奖
评论
