Python数学建模系列（七）：差分
1 递推关系-酵母菌生长模型
差分方程建模的关键在于如何得到第n组数据与第n+1组数据之间的关系
如图所示我们用培养基培养细菌时，其数量变化通常会经历这四个时期。
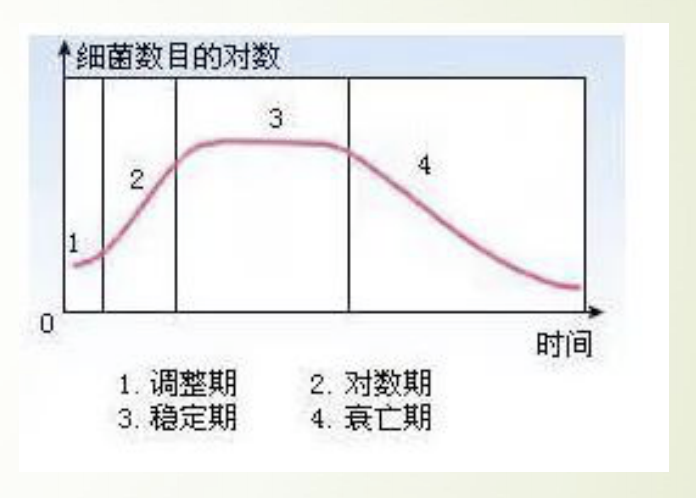这个模型针对前三个时期建一个大致的模型：
调整期 对数期 稳定期
根据已有的数据进行绘图：
import matplotlib.pyplot as plt
time = [i for i in range(0,19)]
number = [9.6,18.3,29,47.2,71.1,119.1,174.6,257.3,
350.7,441.0,513.3,559.7,594.8,629.4,640.8,
651.1,655.9,659.6,661.8]
plt.title('Relationship between time and number')#创建标题
plt.xlabel('time')#X轴标签
plt.ylabel('number')#Y轴标签
plt.plot(time,number)#画图
plt.show()#显示
分析：
酵母菌数量增长有一个这样的规律:当某些资源只能支撑某个最大限度的种群 数量，而不能支持种群数量的无限增长，当接近这个最大值时，种群数量的增 长速度就会慢下来。
两个观测点的值差△p来表征增长速度 △p与目前的种群数量有关，数量越大，增长速度越快 △p还与剩余的未分配的资源量有关，资源越多，增长速度越快 然后以极限总群数量与现有种群数量的差值表征剩余资源量
模型：
「接下来计算模型表达式 求系数k（已知的情况下）」当把该式子看成「二次曲线」进行拟合时：
import numpy as np
import matplotlib.pylab as plt
p_n = [9.6,18.3,29,47.2, 71.1,119.1, 174.6,
257.3, 350.7, 441.0, 513.3, 559.7, 594.8, 629.4,
640.8, 651.1, 655.9, 659.6]
delta_p = [8.7, 10.7,18.2,23.9, 48,55.5,
82.7, 93.4, 90.3, 72.3, 46.4,35.1,
34.6, 11.4, 10.3,4.8,3.7,2.2]
plt.plot(p_n,delta_p)
poly = np.polyfit(p_n, delta_p, 2)
z = np.polyval(poly,p_n)
print(poly)
plt.plot(p_n, z)
plt.show()
# [-8.01975671e-04 5.16054679e-01 6.41123361e+00]
# k = -8.01975671e-04
运行结果
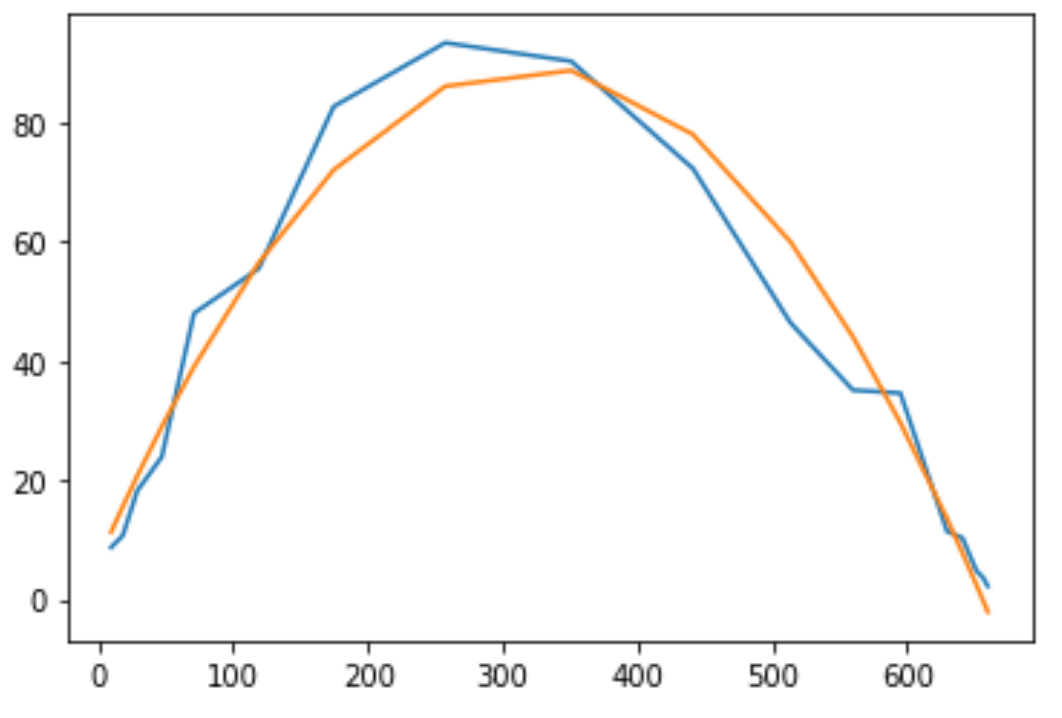
当看成「一次曲线」进行拟合时
❝将 (665 - pn) * pn 看出一个整体 那么整个式子就是一个一次函数
❞
import numpy as np
import matplotlib.pylab as plt
p_n = [9.6,18.3,29,47.2, 71.1,119.1, 174.6,
257.3, 350.7, 441.0, 513.3, 559.7, 594.8, 629.4,
640.8, 651.1, 655.9, 659.6]
delta_p = [8.7, 10.7,18.2,23.9, 48,55.5,
82.7, 93.4, 90.3, 72.3, 46.4,35.1,
34.6, 11.4, 10.3,4.8,3.7,2.2]
p_n = np.array(p_n)
x= (665 - p_n) * p_n
plt.plot(x,delta_p)
ploy = np.polyfit(x,delta_p,1)
print(ploy)
z = np.polyval(ploy,x)
plt.plot(x,z)
plt.show()
# [ 0.00081448 -0.30791574]
# k = 0.00081448
运行结果
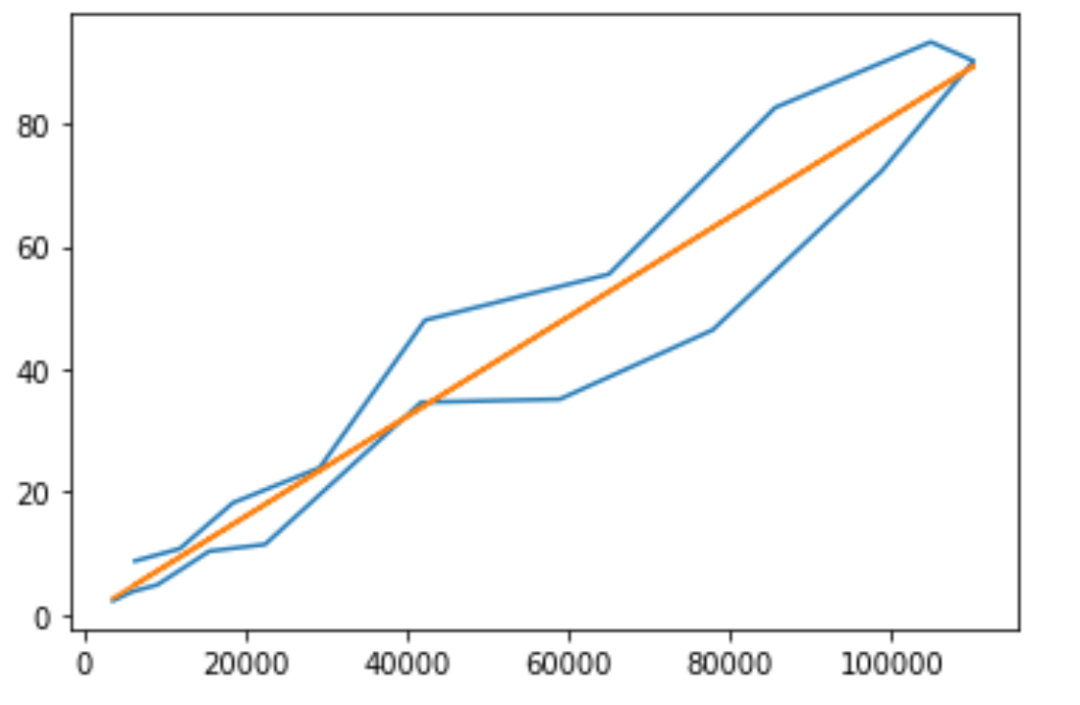
预测曲线：
import matplotlib.pyplot as plt
p0 = 9.6
p_list = []
for i in range(20):
p_list.append(p0)
p0 = 0.00081448*(665-p0)*p0+p0
plt.plot(p_list)
plt.show()
运行结果：
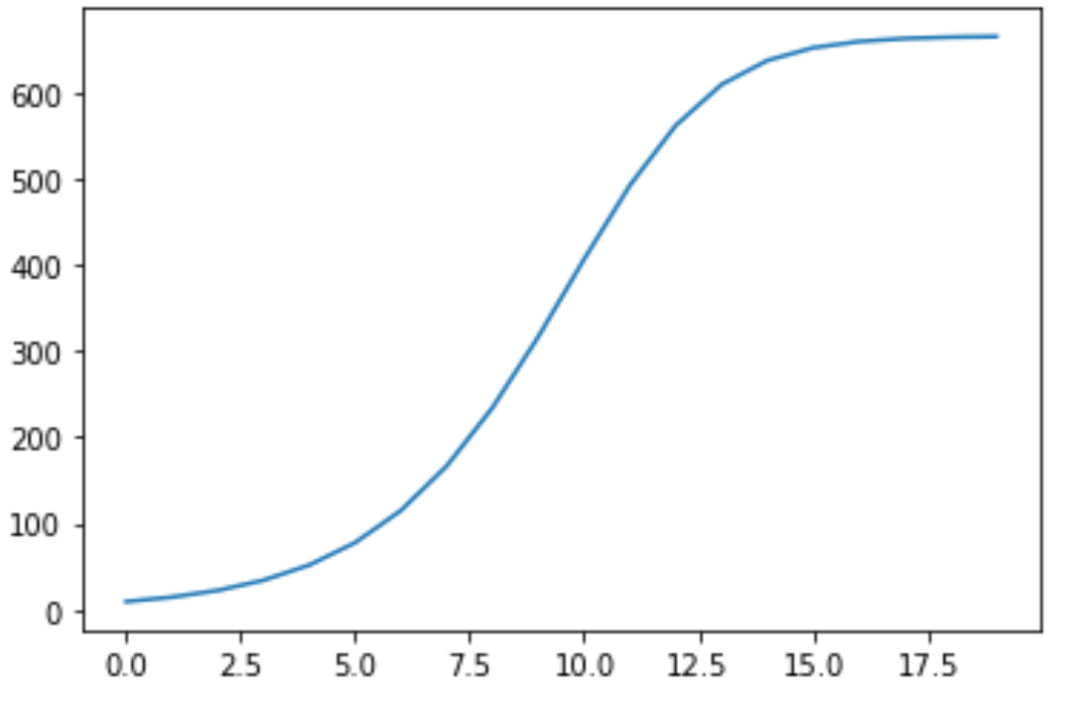
2 显示差分-热传导方程
一维热传导方程为：
❝其中，k为热传导系数，「第2式是方程的初值条件」，第3、4式是边值条件,热传导方程如下：
❞
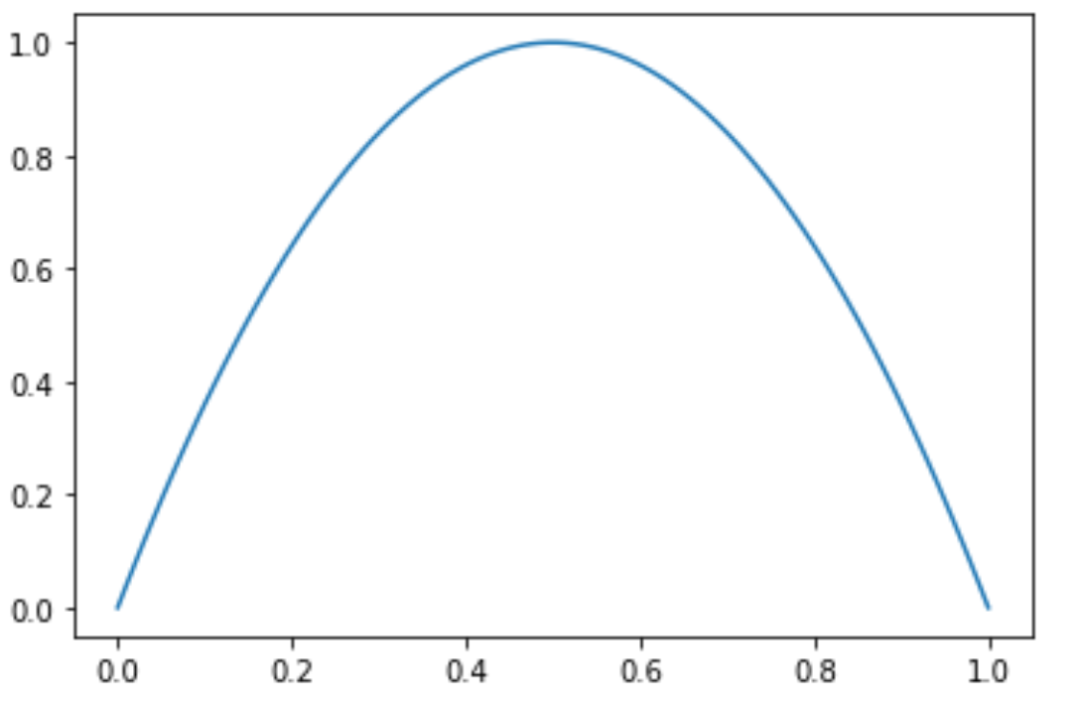
绘制初值条件函数图像（第二个式子）
import numpy as np
import matplotlib.pylab as plt
x = np.linspace(0,1,100)
y = 4 * x * (1 - x)
plt.plot(x,y)
plt.show()
运行结果
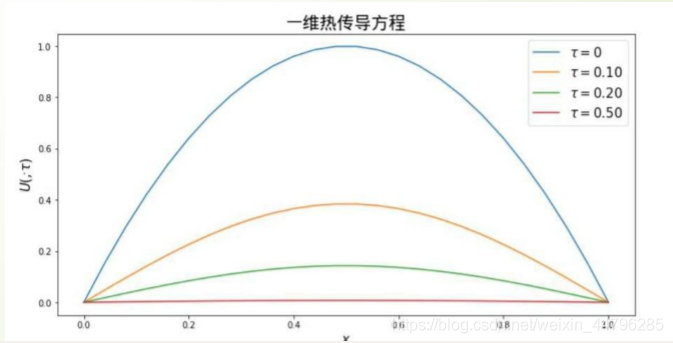
注：CAL库没有安装上，以下代码未运行，照着PPT写了一遍（安装了一天 装上了 但是运行一直报错）
N = 25
M = 2500
T = 1.0
X = 1.0
xArray = np.linspace(0,1.0,50)
yArray = map(initialCondition, xArray)
starValues = yArray
U = np.zeros((N+1,M+1))
U[:,0]=starValues
dx=X/N
dt=T/N
kappa=1.0
rho=kappa*dt/dx/dx
for k in range(0,N):
for j in range(1,N):
U[j][k+1]=rho*U[j-1][k]+ (1.-2*rho)*U[j][k]+ rho*U[j+1][k]
U[0][k+1]=0.
U[N][k+1]=0.
pylab.figure(figsize=(12,6))
pylab.plot(xArray, U[:,0])
pylab.plot(xArray, U[:,int(0.10/dt)])
pylab.plot(xArray, U[:,int(0.20/dt)])
pylab.plot(xArray, U[:,int(0.50/dt)])
pylab.xlabel(‘$x$’, fontsize=15)
pylab.ylabel(r‘$U(\dot,\tau)$’,fontsize=15)
pylab.title(u’一维热传导方程’，fontproperties=font)
pylab.legend([r’$\tau=0.$’, r’$\tau=0.10$’, r’$\tau=0.20$’, r’$\tau=0.50$’],fontsize=15)
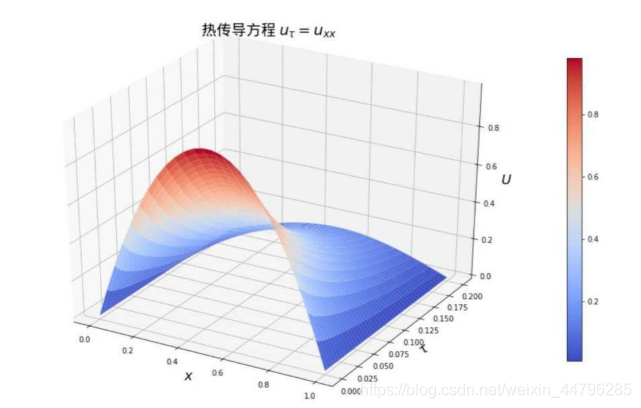
三维立体图查看整体热传导过程 ：
tArray = np.linspace(0, 0.2, int(0.2/dt)+1)
xGride, tGride = np.meshgrid(xArray, tArray)
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = pylab.figure(figsize=(16,10))
ax = fig.add_subplot(1,1,1,projection=‘3d’)
surface = ax.plot_surface(xGride, tGride, U[:,:int(0.2/dt)+1].T, cmap=cm.coolwarm)
ax.set_xlabel(“$x$”, fontdict={“size”:18})
ax.set_ylabel(r“$\tau$”, fontdict={“size”:18})
ax.set_zlabel(r”$U$”, fontdict={“size”:18})
ax.set_title(u”热传导方程 $u_\\tau = u_{xx}$”, fontproperties=font)
fig.colorbar(surface, shrink=0.75)
3 马尔科夫链-选举投票预测
马尔科夫链是由具有以下性质的一系列事件构成的过程：
一个事件有有限多个结果，称为状态，该过程总是这些状态中的一个； 在过程的每个阶段或者时段，一个特定的结果可以从它现在的状态转移到任 何状态，或者保持原状； 每个阶段从一个状态转移到其他状态的概率用一个转移矩阵表示，矩阵每行 的各元素在0到1之间，每行的和为1。
实例：选举投票预测 以美国大选为例，首先取得过去十次选举的历史数据，然后根据历史数据得到 选民意向的转移矩阵。
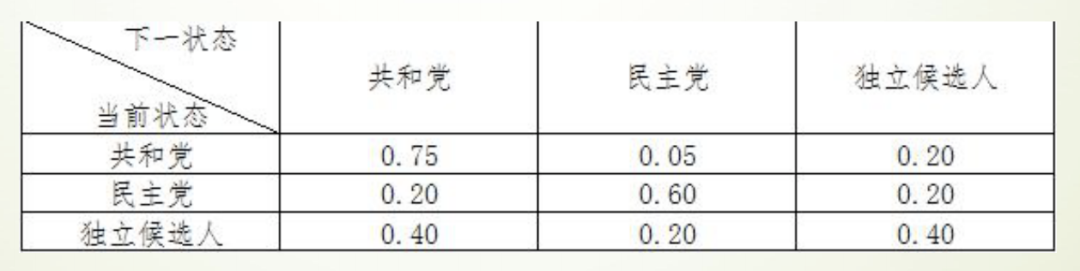
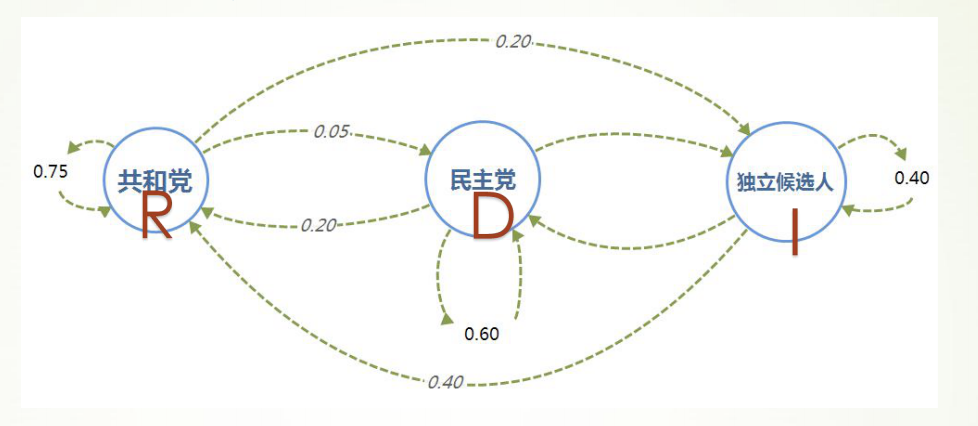
构建差分方程：
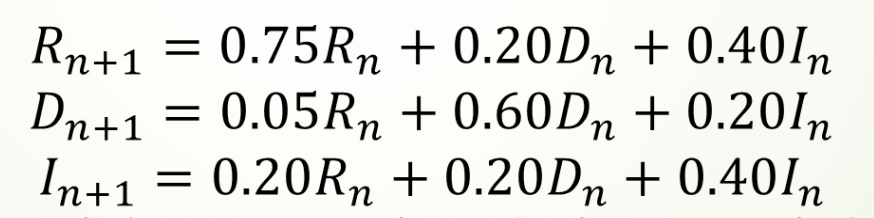
于是可以通过求解差分方程组，推测出选民投票意向的长期趋势
import matplotlib.pyplot as plt
RLIST = [0.33333]
DLIST = [0.33333]
ILIST = [0.33333]
for i in range(40):
R = RLIST[i]*0.75+DLIST[i]*0.20+ILIST[i]*0.40
RLIST.append(R)
D = RLIST[i]*0.05+DLIST[i]*0.60+ILIST[i]*0.20
DLIST.append(D)
I = RLIST[i]*0.20+DLIST[i]*0.20+ILIST[i]*0.40
ILIST.append(I)
plt.plot(RLIST)
plt.plot(DLIST)
plt.plot(ILIST)
plt.xlabel('Time')
plt.ylabel('Voting percent')
plt.annotate('DemocraticParty',xy = (5,0.2))
plt.annotate('RepublicanParty',xy = (5,0.5))
plt.annotate('IndependentCandidate',xy = (5,0.25))
plt.show()
print(RLIST,DLIST,ILIST)
运行结果
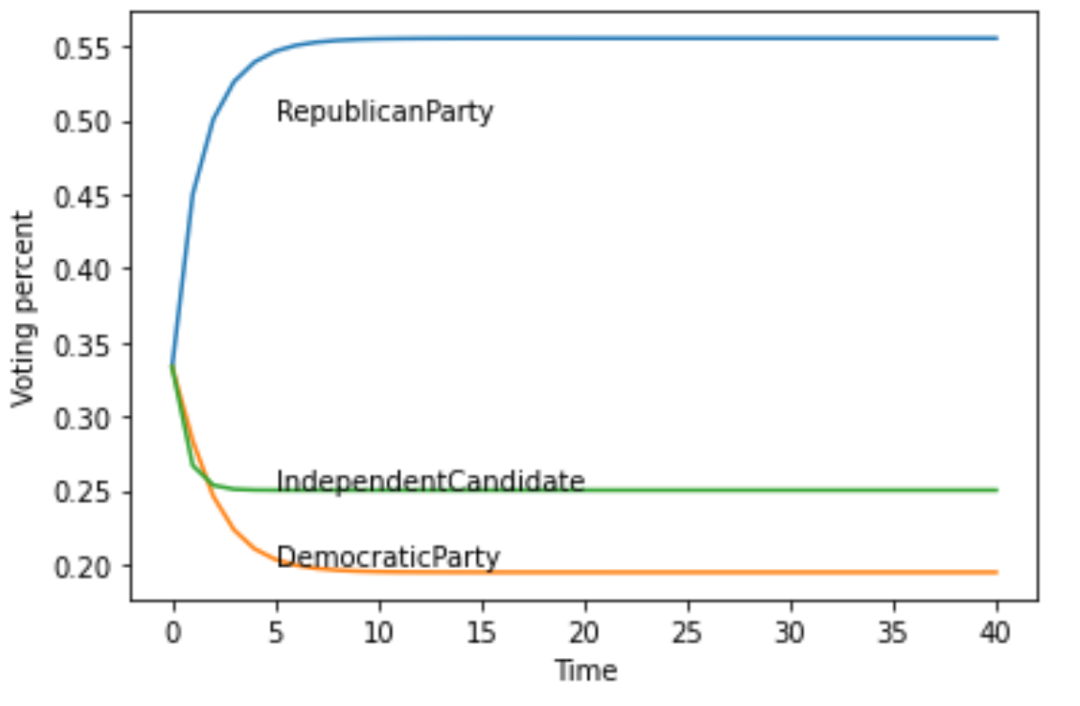
最后得到的长期趋势是：
56%的人选共和党 19%的人选民主党 25%的人选独立候选人
这个问题还可以用「C-K方程」来解
import numpy as np
a = np.array([[0.75,0.05,0.20],[0.20,0.60,0.20],[0.40,0.20,0.40]])
p = np.mat(a)
for i in range(40):
p = p*p
print(p)
运行结果：
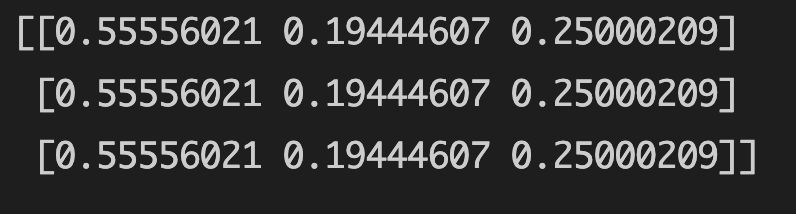
结语
参考：
https://www.bilibili.com/video/BV12h411d7Dm https://www.jianshu.com/p/aa477a3ebf08
学习来源：B站及其课堂PPT，对其中代码进行了复现
「文章仅作为学习笔记，记录从0到1的一个过程」
希望对您有所帮助，如有错误欢迎小伙伴指正～
评论