01trie 在面试中的妙用
简介
就是把整数的二进制表达式当作字符串,之前写过一篇字典树,按照从高位到低位的顺序,挂载在字典树上,每个节点有两个孩子,分别是 ,从而形成一棵二叉树,常用来处理异或问题
例如将一个数组 挂在 上,便得到如下所示的一棵二叉树
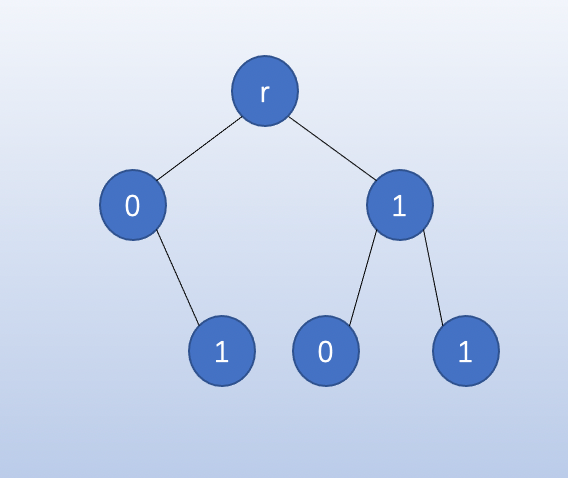
性质
由于 是一棵二叉树,且最大深度取决于挂载值的大小,设挂载最大值为 ,那么一次查询前缀的过程便可以在 时间完成
例题
力扣 421. 数组中两个数的最大异或值
给定 个正整数的数组 ,计算 的最大值
数据规定
题解
将数组中所有正整数的二进制表示,按照从高位到低位的顺序,当作字符串挂载在字典树上,形成 字典树,该字典树为一棵二叉树
对于正整数 ,为了寻找数组中的 ,使得 最大,我们只要每次贪心走与当前位相反的路即可
具体来讲,如果当前位为 ,我们走 子树,反之走 子树,当然,如果不存在对应的子树,我们还是得走存在的子树
这样可以保证异或后的高位尽可能为 ,在二进制表示中,高位为 ,即使剩下的全 ,结果也要比高位为 ,剩下的全 结果大,直观的感受,,这便证明了贪心的正确性
时间复杂度为 ,其中
// cpp
const int N = 2e4;
const int M = 31;
class Solution {
public:
int node[N * M][2], cnt = 0;
void insert(int x)
{
int p = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
if (!node[p][idx]) node[p][idx] = ++cnt;
p = node[p][idx];
}
}
int query(int x)
{
int p = 0;
int ans = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
if (node[p][idx ^ 1]) {
ans *= 2, ans += 1;
p = node[p][idx ^ 1];
}
else {
ans *= 2, ans += 0;
p = node[p][idx];
}
}
return ans;
}
int findMaximumXOR(vector<int>& nums) {
for (auto &i: nums) insert(i);
int ans = 0;
for (auto &i: nums) ans = max(ans, query(i));
return ans;
}
};
力扣 1707. 与数组中元素的最大异或值
给定 个正整数的数组 ,给定 个询问,每个询问包含两个正整数
对于每一个询问,在 中所有不大于 的数中选一个 ,使得 最大,返回这个最大值
数据规定
题解
离线查询,对 从小到大排序,对 按照 从小到大排序
根据单调性,使用双指针,将 中符合条件的正整数 挂载到字典树上,进行查询即可
时间复杂度为 ,其中
// cpp
#define pb push_back
const int N = 1e5;
const int M = 30;
class Solution {
public:
int node[N * M][2], cnt = 0;
void insert(int x)
{
int p = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
if (!node[p][idx]) node[p][idx] = ++cnt;
p = node[p][idx];
}
}
int query(int x)
{
int p = 0;
int ans = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
if (node[p][idx ^ 1]) {
ans *= 2, ans += 1;
p = node[p][idx ^ 1];
}
else {
ans *= 2, ans += 0;
p = node[p][idx];
}
}
return ans;
}
vector<int> maximizeXor(vector<int>& nums, vector<vector<int>>& q) {
int idx = 0;
for (auto &i: q) i.pb(idx++);
sort(q.begin(), q.end(), [&](const vector<int> &x, const vector<int> &y){
return x[1] < y[1];
});
sort(nums.begin(), nums.end());
int n = q.size();
vector<int> ans(n);
for (int i = 0, j = 0; i < n; ++i) {
while (j < nums.size() && nums[j] <= q[i][1])
insert(nums[j++]);
if (!j) ans[q[i][2]] = -1;
else ans[q[i][2]] = query(q[i][0]);
}
return ans;
}
};
力扣 1938. 查询最大基因差
给定一棵 个节点的树,每个节点的编号 即为其权值
给定 个查询,每个查询包含树上一个点的编号 和目标值
对于每一个查询,你需要选一个从根到 的节点 ,要求使得 值最大,返回这个最大值
数据规定
题解
离线查询,维护每个节点的所有查询
我们需要维护一个从根到当前节点的路径,因此考虑 dfs
具体来讲,深搜到当前点 时,将 挂载在 01 trie 上,同时进行一次查询,计算出最大的异或值,继续向下深搜,等到回溯的时候,将当前节点的权值从字典树上删除
计算最大异或值时,每次贪心选择与当前位相反的节点即可
时间复杂度为 ,其中
// cpp
#define pii pair< int, int >
#define fi first
#define se second
#define pb push_back
const int N = 2e5;
const int M = 18;
int node[N * M][2], bucket[N * M][2], cnt = 0;
void insert(int x)
{
int p = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
if (!node[p][idx]) node[p][idx] = ++cnt;
bucket[p][idx]++;
p = node[p][idx];
}
}
void del(int x)
{
int p = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
int next = node[p][idx];
if (bucket[p][idx] == 1) node[p][idx] = 0;
bucket[p][idx]--;
p = next;
}
}
int query(int x)
{
int p = 0;
int ans = 0;
for (int i = M; i >= 0; --i) {
int idx = 1 & (x >> i);
if (node[p][idx ^ 1]) {
ans *= 2, ans += 1;
p = node[p][idx ^ 1];
}
else {
ans *= 2, ans += 0;
p = node[p][idx];
}
}
return ans;
}
class Solution {
public:
unordered_map< int, vector< pii > > mp;
vector< int > son[N];
void dfs(int u, vector< int > &ans)
{
insert(u);
for (auto &i : mp[u]) ans[i.se] = query(i.fi);
for (auto &i : son[u]) dfs(i, ans);
del(u);
}
vector< int > maxGeneticDifference(vector< int > &p, vector< vector< int > > &q)
{
int root = 0;
for (int i = 0; i < p.size(); ++i) {
if (p[i] != -1)
son[p[i]].push_back(i);
else
root = i;
}
int n = q.size();
for (int i = 0; i < n; ++i) {
q[i].pb(i);
mp[q[i][0]].pb({ q[i][1], q[i][2] });
}
vector< int > ans(n);
dfs(root, ans);
return ans;
}
};
