计算机是如何起源的?

人类的历史可以看做一部关于解放的历史。也有这样的说法,懒惰是人类进步的动力。为了偷懒,人类不断的做着各种努力,发明了各种机器工具,将自己从繁重的劳动解放出来,另一方面,每一次大的进步,都需要解放思想,同时也带来了全人类思想的大解放。在这样的历程中,计算机的出现无疑将人类从很多繁重的作业中解放了出来。与此同时,有些人开始思考能否制造出可以像人类一样进行思考的机器,以将人类从创造性的劳动和逻辑思考中解放出来,交给机器去完成。
>>>>

虽然计算机的出现,不到百年,然而为了它的出现,所进行的探索和研究,早已经历经数百年的历史。当然准确的说,这些探索和研究在当时实际并不是为了计算机产生而进行的,绝大多数只是做了一个无意的铺垫。或许我们并不熟悉这样的一个过程,老实说现代的大学教育中也很少提及计算机出现之前的那些历史。实际上,了解这样的一个过程,更有助于我们理解一个事物是如何产生出来,它背后的科学原理又是如何,让我们可以透过复杂的电路外表,接触到最本质的东西。可以让我们除了对科学家们的工作表示赞叹之外,也可以深入他们当初的思想过程,近距离地进行跨越时间和空间的沟通。这对于我们自己应该如何思考问题,创造性地提出自己的想法也是有所帮助的。
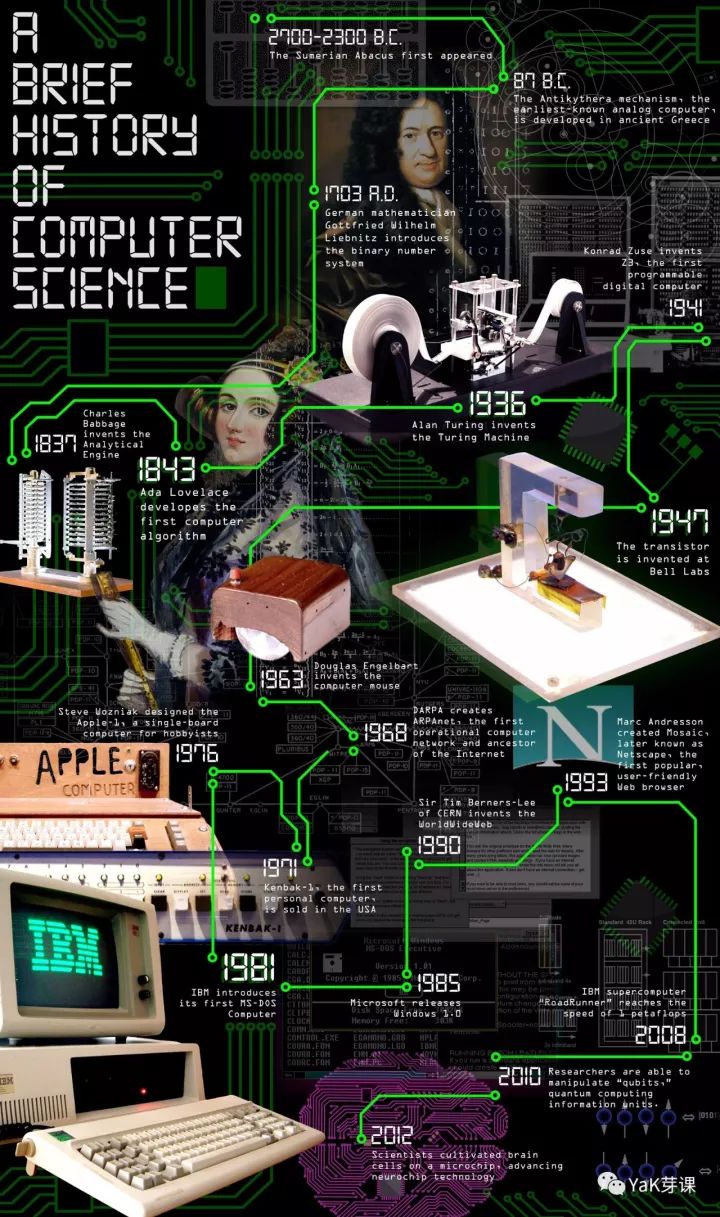
我们已经了解到这样的一些人物,乔治.布尔,康托,哥德尔,图灵,冯诺依曼。而我们的离散数学的教学中,本身太注重于知识本身的学习,而忽略了知识是如何被发现产生出来,以及不同的知识之间曾经的渊源和启发关系。而对于启迪思想来说,后者显然更为有力。

莱布尼茨之梦
布尔的逻辑代数

现在我们以逻辑代数的观点看这个式子,它体现了这样一个含义:没有任何东西可以同时属于又不属于某个类。这点让布尔十分振奋,因为这刚好体现了亚里士多德的排中律,这就使他确信自己找对了路子。
所有y都是z y=yz
------------ ?
所有x都是z x=xz
x=xy
y=yz => x = xy = x(yz) = (xy)z = xz

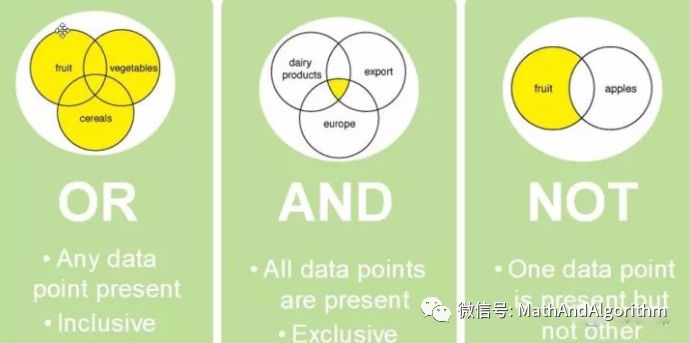
今天的布尔代数
AND | 1 0 ----------------------- 1 | 1 0 0 | 0 0
OR | 1 0 ----------------------- 1 | 1 1 0 | 1 0
NOT | -------------- 1 | 0 0 | 1

弗雷格的突破与绝望

康托尔,对无限的探索

大卫希尔伯特

哥德尔完备性定理
U说某个特殊命题在PM中不可证。
那个特殊的命题就是U本身。
因此,U说"U在PM中不可证"
图灵和图灵机
找到一种算法,判定一个给定的自然数是否属于集合D。
- END -
评论
