谈谈神经网络的大规模训练优化-轻识

文 | 立交桥跳水冠军

源 | 知乎

大规模神经网络训练一般会涉及到几百个分布式节点同时工作，模型的参数量以及运算量往往很大，作者认为在这个task下当前的工作主要归结为以下三种：对通信本身的优化，神经网络训练通信的优化，大规模下如何保持精度。

之前一段时间接触了大规模神经网络训练，看了不少优秀的工作，在这里当做笔记记下来。同时也希望可以抛砖引玉，和各位大佬交流一下这方面的现有工作以及未来的方向（1）大规模训练工作的几种类型大规模训练和普通分布式训练还是有区别的，主要体现在大这个字上面。一般来说会涉及到几百个分布式节点同时工作，模型的参数量以及运算量往往很大（比如BERT，GPT3等等）我认为在这个task下当前的工作主要归结为以下三种：

对通信本身的优化
神经网络训练通信的优化
大规模下如何保持精度

其中1主要是通信库的优化，严格来说和神经网络本身并没有关系，这里面比较优秀的工作有经典的ring-base all-reduce（最先在百度的工作中被用于神经网络训练baidu-research/baidu-allreduce：

https://github.com/baidu-research/baidu-allreduce

腾讯的分层通信：

https://arxiv.org/abs/1807.11205

以及sony的2D all-reduce（Massively Distributed SGD: ImageNet/ResNet-50 Training in a Flash：

https://arxiv.org/abs/1811.05233

而第2部分的工作都针对于如何在神经网络这个训练模式下做通信优化。这方面的思路很广，比如商汤提出的稀疏通信：

https://arxiv.org/abs/1902.06855

杜克大学提出的TernGrad (TernGrad: Ternary Gradients to Reduce Communication in Distributed Deep Learning：

https://arxiv.org/abs/1705.07878

第三部分和前两个不同，主要关注点在于精度而非性能。在大规模训练的情况下，一种常见的做法是做数据并行，即把batch size设的很大，那么原来跑90个epoch需要迭代1000次的话，把batch size扩大10倍，就只需要迭代100次，即参数的更新次数减少了很多。如何在这种情况下收敛到小batch size也是一个棘手的问题。在这个领域比较好的工作有face book的线性倍增学习率（https://arxiv.org/pdf/1706.02677.pdf）以及伯克利尤洋的LAR算法（https://arxiv.org/pdf/1709.05011.pdf）。

对通信本身的优化

（懒得写了，偷个懒）我对这方面了解十分有限，推荐大家读腾讯团队写的介绍（兰瑞Frank：腾讯机智团队分享--AllReduce算法的前世今生：
https://zhuanlan.zhihu.com/p/79030485

神经网络的通信优化

分布式神经网络训练目前主要有两种模式：数据并行和模型并行。

数据并行比较简单，下面这张图是经典的数据并行的同步训练的场景：所有节点（即图中的GPU0-GPU3）都保存整个模型(粉色的Params)，每次迭代，不同的节点会得到不同的数据，每个节点用得到的数据做正向和反向计算，得到每个参数的梯度。之后整个分布式系统会同步所有节点的梯度，即每个节点的local gradient做一次all reduce操作，得到全局的global gradient（最下面蓝色的Gradients）。每个节点用这个global gradient更新参数。

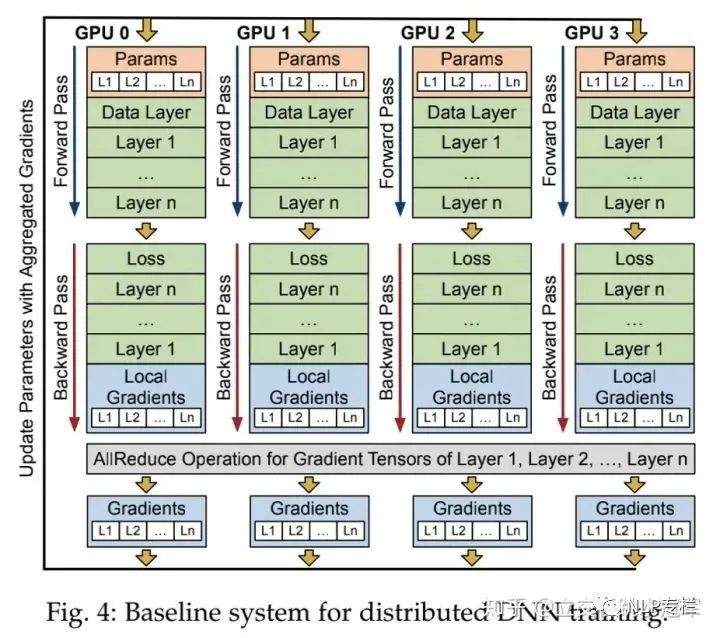
显而易见，数据并行基于一个假设：每个节点都可以放下整个模型。这个假设在如今某些模型上（说的就是你，GPT3！！！）是不合理的，因此我们还需要模型并行，即不同节点负责计算神经网络模型的不同部分（比如有一个100层的网络，那么我们可以让第一个节点存储前50层的参数，并负责计算前50层，另一个网络则负责后面50层）。

下面这张图摘自英伟达的Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism:
https://arxiv.org/abs/1909.08053

在这里演示了如何用两个节点去算连续的两个矩阵乘法。

我们要做的操作是首先算出Y=GeLU(XA)，再算Z=Dropoug(YB)。其中，X，A，B都是矩阵，而且矩阵规模都很大。

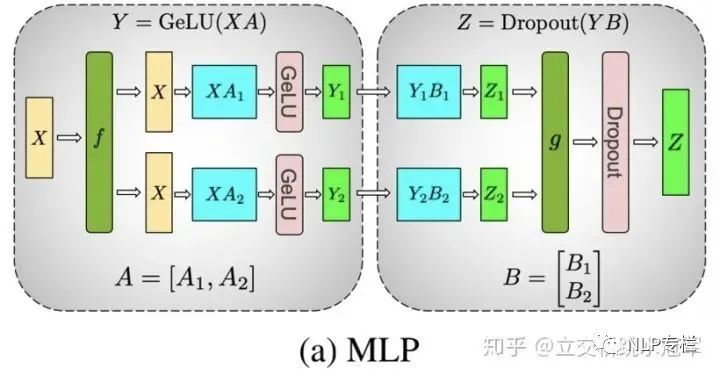
假设我们希望用两个分布式节点完成这个计算，那么我们可以把矩阵A按colum切成A1，A2两份，分别存到节点0和节点1中。同时我们也把矩阵B按行切成B1，B2两份，分别存到节点0和节点1中。然后我们将X做一个broadcast（图中f部分），分别发送到两个节点上，算得Z1和Z2，在做一次all reduce（图中g部）将Z1和Z2相加，得到最终的Z。

这里面有一个很巧（也很绕）的地方，那就是为什么A要按列切，B要按行切？我们可不可以把它们反过来？答案是：最好不要，因为如果反过来，的确计算上可行，但是我们就会增加一次通信（即算Y=XA的时候我们就要做一次通信），这样显然速度会变慢。

展开来讲，数据并行和模型并行也可以细分。数据并行可以分为：

同步式数据并行
异步式数据并行

同步式比较简单，就是我最上面那张图演示的。

异步式复杂一些：我们很容易发现，最后全局all reduce gradient的时候会耗时比较多，分布式系统越大，消耗越大，而且这样做还有一个隐藏的假设：分布式系统是homogeneous的，即每个分布式节点不会差的很多。举个例子，如果每个节点实力相当，那么都会算10s就可以结束一个iteration，那么我们10s之后就可以开始一次通信。然而如果有一个节点（害群之马）需要算100s，那么其他节点算完之后就得干等它90s才能做通信，那么是对资源的极大浪费。

想想看，你的老板绝对不允许你（打工人）干坐着什么事都不干，只因为你的进度被别的同事block了。研究员也是如此，于是为了解决上面的问题，引入了异步式通信。简单来说就是如果遭遇了上面的情况，快的节点等一会儿就不等了，他们之间做一次通信然后接着算下一轮。这个节点什么时候算好什么时候再和其他人一起all reduce梯度。

这样做快是快了，但引入了另一个问题，那就是每个人的参数都不一样了，那么他们根据不同的参数算得的梯度再去做all reduce就有一些不合理，就会导致神经网络精度受损。

有很多工作尝试解决异步并行带来的精度损失，不过据我所知并没有特别general的方法，因此异步并行如今也很少被使用了。模型并行可以分为：

粗粒度并行
细粒度并行

它们的区别在于并行的层级：粗粒度每个节点会算不同的layer，而细粒度会将layer也做拆。

分粗粒度并行比较优秀的工作有google的GPipe(https://arxiv.org/pdf/1811.06965.pdf)

在粗粒度并行中，每个节点负责不同的layer，但是layer之间是存在数据依赖的，这就导致在之前的节点算的时候，后面的节点干等着。GPipe提出把数据按照batch纬度做切分得到多个micro batch，这样第一个节点先算第一个micro batch（图中F[0,0]），把算到的结果发给第二个节点去算，于是下一个时刻第二个节点在算第一个micro batch(F[1,0])，而第一个节点开始算第二个micro batch(F[0,1])。

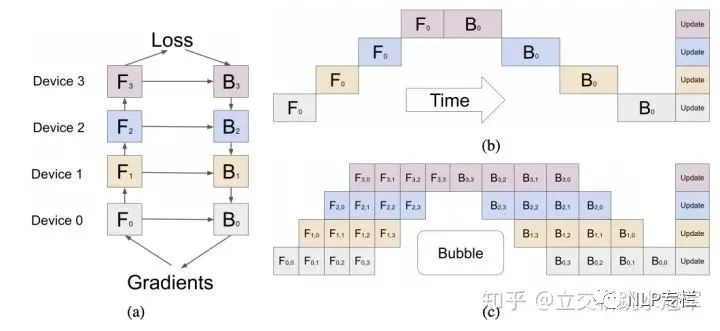
细粒度并行比较好的工作除了我之前介绍的Megatron之外，还有GShard(GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding（https://arxiv.org/abs/2006.16668)

这个工作主要的贡献在于提供了一套原语，允许最高层的开发者（写python的人）通过简单的方式指导代码生成（即编译器）生成对应的模型并行的代码。