时间序列的平稳性检验方法
当我们有一个新的时间序列数据时,怎么判断它是否是平稳的呢?
时间序列平稳性检验方法,可分为三类:
图形分析方法 简单统计方法 假设检验方法
一、图形分析方法
图形分析方法是一种最基本、最简单直接的方法,即绘制图形,肉眼判断。
可直接可视化时间序列数据,也可以可视化时间序列的统计特征。
可视化数据
可视化数据即绘制时间序列的折线图,看曲线是否围绕某一数值上下波动(判断均值是否稳定),看曲线上下波动幅度变化大不大(判断方差是否稳定),看曲线不同时间段波动的频率[~紧凑程度]变化大不大(判断协方差是否稳定),以此来判断时间序列是否是平稳的。
以下绘制几张图,大家来直观判断一下哪些是平稳的,哪些是非平稳的。
import numpy as np
import pandas as pd
import akshare as ak
from matplotlib import pyplot as plt
np.random.seed(123)
# -------------- 准备数据 --------------
# 白噪声
white_noise = np.random.standard_normal(size=1000)
# 随机游走
x = np.random.standard_normal(size=1000)
random_walk = np.cumsum(x)
# GDP
df = ak.macro_china_gdp()
df = df.set_index('季度')
df.index = pd.to_datetime(df.index)
gdp = df['国内生产总值-绝对值'][::-1].astype('float')
# GDP DIFF
gdp_diff = gdp.diff(4).dropna()
# -------------- 绘制图形 --------------
fig, ax = plt.subplots(2, 2)
ax[0][0].plot(white_noise)
ax[0][0].set_title('white_noise')
ax[0][1].plot(random_walk)
ax[0][1].set_title('random_walk')
ax[1][0].plot(gdp)
ax[1][0].set_title('gdp')
ax[1][1].plot(gdp_diff)
ax[1][1].set_title('gdp_diff')
plt.show()
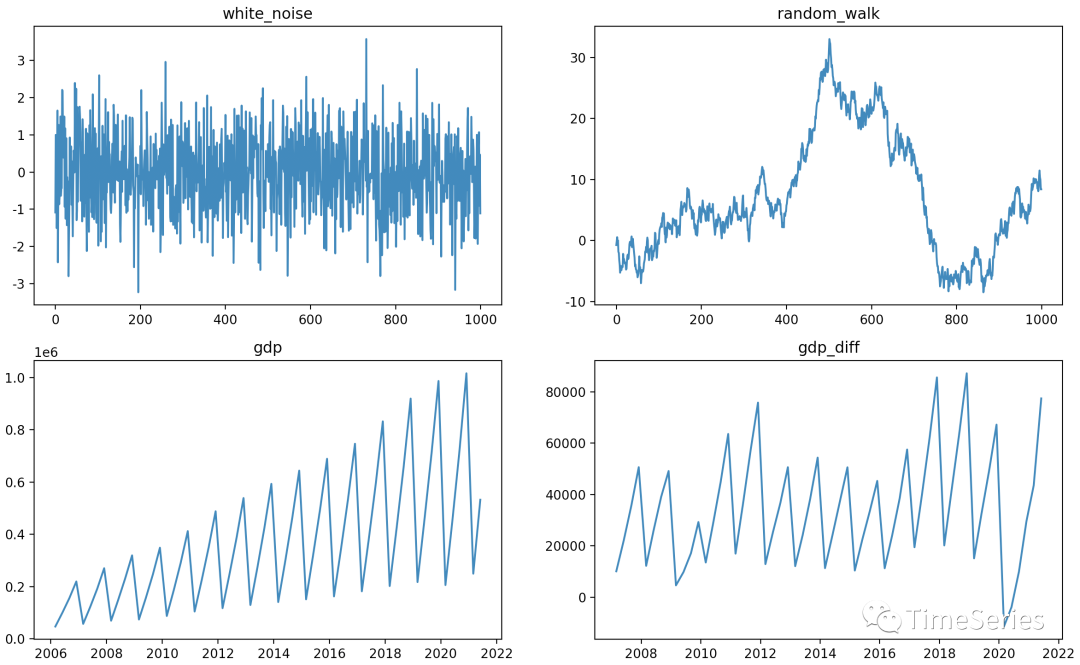 a. 白噪声,曲线围绕0值上下波动,波动幅度前后、上下一致,为平稳序列。
a. 白噪声,曲线围绕0值上下波动,波动幅度前后、上下一致,为平稳序列。
b. 随机游走,曲线无确定趋势,均值、方差波动较大,非平稳序列。
c. GDP数据趋势上升,均值随时间增加,非平稳序列。
d. GDP季节差分后数据,曲线大致在一条水平线上上下波动,波动幅度前后变化较小,可认为是平稳的。
可视化统计特征
可视化统计特征,是指绘制时间序列的自相关图和偏自相关图,根据自相关图的表现来判断序列是否平稳。
自相关,也叫序列相关,是一个信号与自身不同时间点的相关度,或者说与自身的延迟拷贝--或滞后--的相关性,是延迟的函数。不同滞后期得到的自相关系数,叫自相关图。
(这里有一个默认假设,即序列是平稳的,平稳序列的自相关性只和时间间隔k有关,不随时间t的变化而变化,因而可以称自相关函数是延迟(k)的函数)
平稳序列通常具有短期相关性,对于平稳的时间序列,自相关系数往往会迅速退化到零(滞后期越短相关性越高,滞后期为0时,相关性为1);而对于非平稳的数据,退化会发生得更慢,或存在先减后增或者周期性的波动等变动。

自相关的计算公式为根据滞后期k将序列拆成等长的两个序列,计算这两个序列的相关性得到滞后期为k时的自相关性。举例:
import statsmodels.api as sm
X = [2,3,4,3,8,7]
print(sm.tsa.stattools.acf(X, nlags=1, adjusted=True))
> [1, 0.3559322]
其中第一个元素为滞后期为0时的自相关性,第二个元素为滞后期为1时的自相关性
根据ACF求出滞后k自相关系数时,实际上得到并不是X(t)与X(t-k)之间单纯的相关关系。
因为X(t)同时还会受到中间k-1个随机变量X(t-1)、X(t-2)、……、X(t-k+1)的影响,而这k-1个随机变量又都和X(t-k)具有相关关系,所以自相关系数里面实际掺杂了其他变量对X(t)与X(t-k)的影响。
在剔除了中间k-1个随机变量X(t-1)、X(t-2)、……、X(t-k+1)的干扰之后,X(t-k)对X(t)影响的相关程度,叫偏自相关系数。不同滞后期得到的偏自相关系数,叫偏自相关图。(偏自相关系数计算较复杂,后期再来具体介绍)
下面我们就来看看几个实战案例(上图中的数据再来看一下它们的自相关图和偏自相关图):
# 数据生成过程在第一个代码块中
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
fig, ax = plt.subplots(4, 2)
fig.subplots_adjust(hspace=0.5)
plot_acf(white_noise, ax=ax[0][0])
ax[0][0].set_title('ACF(white_noise)')
plot_pacf(white_noise, ax=ax[0][1])
ax[0][1].set_title('PACF(white_noise)')
plot_acf(random_walk, ax=ax[1][0])
ax[1][0].set_title('ACF(random_walk)')
plot_pacf(random_walk, ax=ax[1][1])
ax[1][1].set_title('PACF(random_walk)')
plot_acf(gdp, ax=ax[2][0])
ax[2][0].set_title('ACF(gdp)')
plot_pacf(gdp, ax=ax[2][1])
ax[2][1].set_title('PACF(gdp)')
plot_acf(gdp_diff, ax=ax[3][0])
ax[3][0].set_title('ACF(gdp_diff)')
plot_pacf(gdp_diff, ax=ax[3][1])
ax[3][1].set_title('PACF(gdp_diff)')
plt.show()
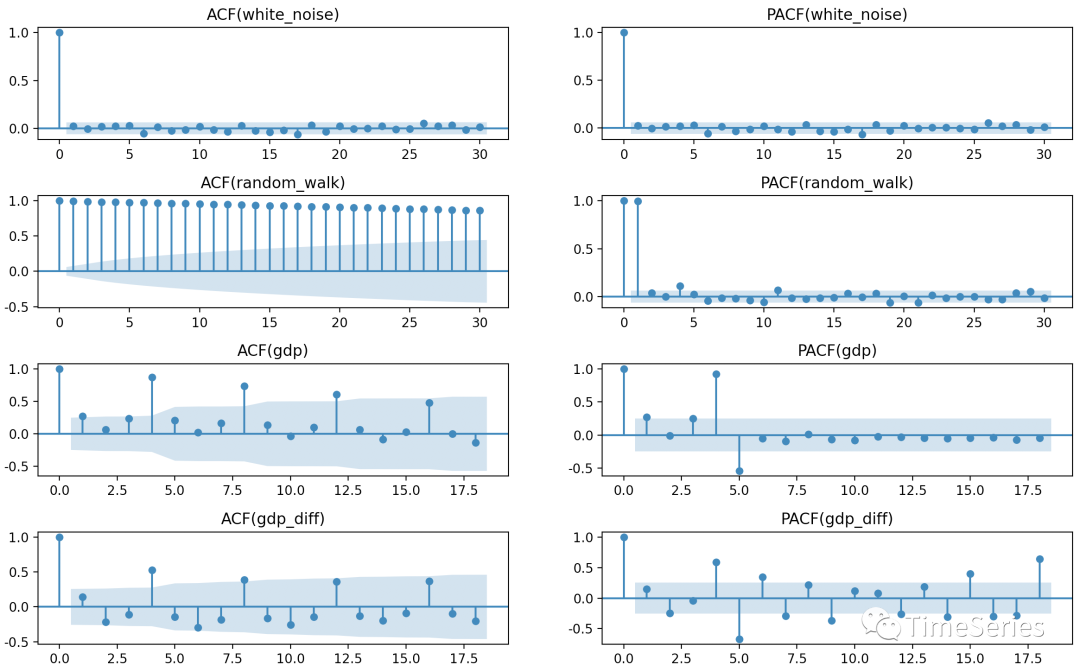 (1) 白噪声的自相关系数很快就衰减到0附近,是明显的平稳序列。滞后期为0时自相关系数和偏自相关系数其实就是序列自己和自己的相关性,故为1;滞后期为1时,自相关系数为0,表示白噪声无自相关性。
(1) 白噪声的自相关系数很快就衰减到0附近,是明显的平稳序列。滞后期为0时自相关系数和偏自相关系数其实就是序列自己和自己的相关性,故为1;滞后期为1时,自相关系数为0,表示白噪声无自相关性。
(2) 随机游走,自相关系数下降非常缓慢,故为非平稳序列;另从偏自相关系数中可以看到随机游走只和前一项有关。
(3) GDP数据的自相关图中也可以看到存在一定的周期性,滞后4、8、12等自相关系数较大下降较慢,差分后下降多一些起到一定效果,认为差分后序列是平稳的。同可视化数据一样,直观判断带有较强主观性,但能让我们对数据有更直观的认识。
二、简单统计方法
计算统计量的方法只是作为一个补充,了解即可。宽平稳中有两个条件是均值不变和方差不变,可视化数据中我们可以直观看出来,其实还可以具体计算一下看看。
很有意思的逻辑,直接将序列前后拆分成2个序列,分别计算这2个序列的均值、方差,对比看是否差异明显。(其实很多时序异常检验也是基于这种思想,前后分布一致则无异常,否则存在异常或突变)
我们来算白噪声和随机游走序列不同时间段的均值、方差:
import numpy as np
np.random.seed(123)
white_noise = np.random.standard_normal(size=1000)
x = np.random.standard_normal(size=1000)
random_walk = np.cumsum(x)
def describe(X):
split = int(len(X) / 2)
X1, X2 = X[0:split], X[split:]
mean1, mean2 = X1.mean(), X2.mean()
var1, var2 = X1.var(), X2.var()
print('mean1=%f, mean2=%f' % (mean1, mean2))
print('variance1=%f, variance2=%f' % (var1, var2))
print('white noise sample')
describe(white_noise)
print('random walk sample')
describe(random_walk)
white noise sample:
mean1=-0.038644, mean2=-0.040484
variance1=1.006416, variance2=0.996734
random walk sample:
mean1=5.506570, mean2=8.490356
variance1=53.911003, variance2=126.866920
白噪声序列均值和方差略有不同,但大致在同一水平线上;
随机游走序列的均值和方差差异就比较大,因此为非平稳序列。
三、假设检验方法
平稳性的假设检验方法当前主流为单位根检验,检验序列中是否存在单位根,若存在,则为非平稳序列,不存在则为平稳序列。
在介绍检验方法之前,有必要了解一些相关补充知识,这样对后面的检验方法理解上就会更清晰一些。
确定趋势
如果时间序列有“确定趋势”,比如
其中, 即为确定趋势。
期望中有时间变量,随时间变化,所以不是平稳时间序列。
含有确定趋势的序列的差分过程是过度差分:
过度差分不但会使序列样本容量减少,还会使序列的方差变大。差分后的序列会存在自相关性,但这种自相关性是毫无意义的。
所以应该使用“退势”的方法获得平稳序列,如下:
但是 如何确定,趋势拟合。消除序列中的时间趋势后,即为平稳序列,所以称这样的序列为“趋势平稳”序列或“退势平稳”序列。
随机趋势
另一种导致时间序列非平稳的因素为“随机趋势”。比如随机游走模型:
,其中 为白噪声
来自 的任何波动对 都具有永久性的冲击,最主要的是其影响力不随时间而衰减,称 为这个模型的“随机趋势”。
带漂移项的随机游走模型:
, 其中 为常数
除持续受到来自随机趋势 的影响外,还受一个常数项 的影响。
以上对随机游走或带漂移项的随机游走进行一阶差分,均可消除随机趋势的影响,得到一个平稳序列,故称“差分平稳”序列。
d阶单整
称平稳的时间序列为“零阶单整”(Integrated of order zero),记为 。
如果时间序列的一阶差分是平稳的,则称为“一阶单整”(Integrated of order one),记为 ,也称为“单位根过程”(unit root process)。
更一般地,如果时间序列的 阶差分为平稳过程,则称为“d阶单整”(Integrated of order d),记为 。
什么是单位根
考虑如下基础模型:
,其中 为白噪声
和随机游走模型很像,只不过多了个系数 。
我们知道随机游走是非平稳的,但是当 时,这个序列就变成平稳的了。
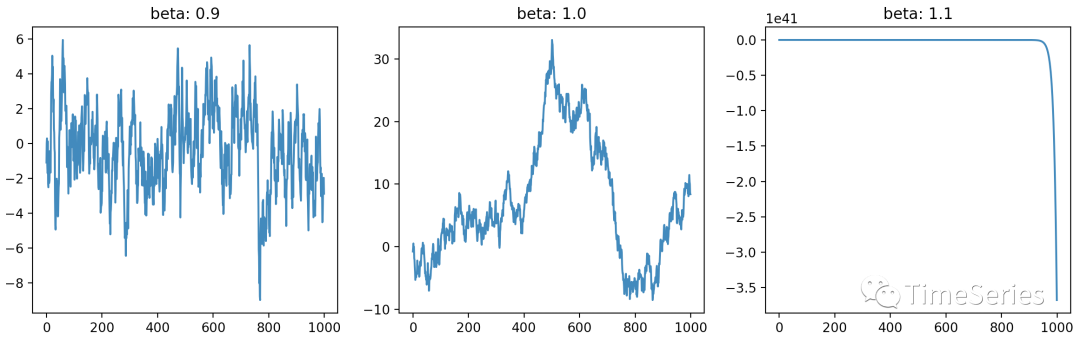
当 时,随着 的增大, 最终会收敛,长期来看 是平稳的。
当 时, 为无规律非平稳的随机游走过程;
当 时, 为爆炸式增长的非平稳过程。
等于1时 就是我们所说的单位根。
画图对比以下可能会更清晰一些
import numpy as np
from matplotlib import pyplot as plt
np.random.seed(123)
def simulate(beta):
y = np.random.standard_normal(size=1000)
for i in range(1, len(y)):
y[i] = beta * y[i - 1] + y[i]
return y
plt.figure(figsize=(20, 4))
for i, beta in enumerate([0.9, 1.0, 1.1]):
plt.subplot(1, 3, i+1)
plt.plot(simulate(beta))
plt.title('beta: {}'.format(beta))
plt.show()
一阶差分方程
为一阶随机差分方程(因为含有随机项)
无随机项为确定性差分方程(但非齐次,因为含常数项 )
为对应的齐次差分方程
根据差分方程理论, 的稳定性和 的稳定性是一样的,而 是否稳定取决于 是否稳定,所以判断一个差分方程是否稳定,只要看它对应的齐次差分方程是否有稳定的通解即可。
以上齐次差分方程对应的特征方程为:, 称为差分方程的特征根。
只有 ,即特征方程的根落在复平面的单位圆以内的时候,过程才会平稳。若果根正好落在圆上,称为单位根,为非平稳过程,比如随机游走的情形。如果落在圆外,则为爆炸式增长的非平稳过程。
差分方程写成滞后算子的形式是这样的
, 为滞后算子
对应特征方程(逆特征方程)为:
, 称为自回归滞后算子多项式的特征根。
显然,差分方程的特征值λ与自回归滞后算子多项式的特征根z是互为倒数。
均小于1(特征方程的根都在单位圆内)时是平稳的,对应的 均大于1(逆特征方程的根都在圆外)时是平稳的。
更一般的n阶差分方程
对应的齐次差分方程为:
该齐次差分方程的特征方程为:
根均在单位圆内是平稳的。
滞后算子形式(逆特征方程)为:
根均在单位圆外是平稳的。
一般直接计算高阶差分方程的根比较复杂,有些简单规则可以用来检验高阶差分方程的稳定性。
n阶差分方程中,所有特征根均位于单位圆内的充分条件为:
n阶差分方程中,所有特征根均位于单位圆内的必要条件为:
如果 ,至少有一个特征根等于1。
一个或多个特征根等于1的时间序列,称为单位根过程。
单位根(unit root)检验就是检验该差分方程的特征方程(characteristic equation)的各个特征根(characteristic root)是均小于1,还是存在等于1的情况。没有检验均大于1的情况,是因为当根均大于1时为爆炸型发散序列,日常数据中基本不存在。
DF检验
ADF检验(Augmented Dickey-Fuller Testing)是最常用的单位根检验方法之一,通过检验序列是否存在单位根来判断序列是否是平稳的。ADF检验是DF检验的增强版,在介绍ADF之前,我们先来看一下DF检验。
迪基(Dickey)和弗勒(Fuller)1979年基于非平稳序列的基本特征将其大致归为三类并提出DF检验:
(1) 当序列基本走势呈现无规则上升或下降并反复时,将其归为无漂移项自回归过程;
(2) 当序列基本走势呈现明显的随时间递增或递减且趋势并不太陡峭时,将其归为带漂移项自回归过程;
(3) 当序列基本走势随时间快速递增时,则将其归为带趋势项回归过程。
对应检验回归式为:
(i) 无漂移项自回归过程:
(ii) 带漂移项自回归过程:
(iii) 带漂移项和趋势项自回归过程:
其中 是常数项, 是时间趋势项, 为白噪声无自相关性。
原假设 (存在单位根,时间序列是非平稳的) 备择假设 (不存在单位根,时间序列是平稳的--不含截距项和趋势项平稳/含截距项平稳/含截距项和趋势平稳)
若检验统计量大于临界值(p值大于显著性水平 ),不能拒绝原假设,序列是非平稳的;
若检验统计量小于临界值(p值小于显著性水平 ),拒绝原假设,认为序列是平稳的。
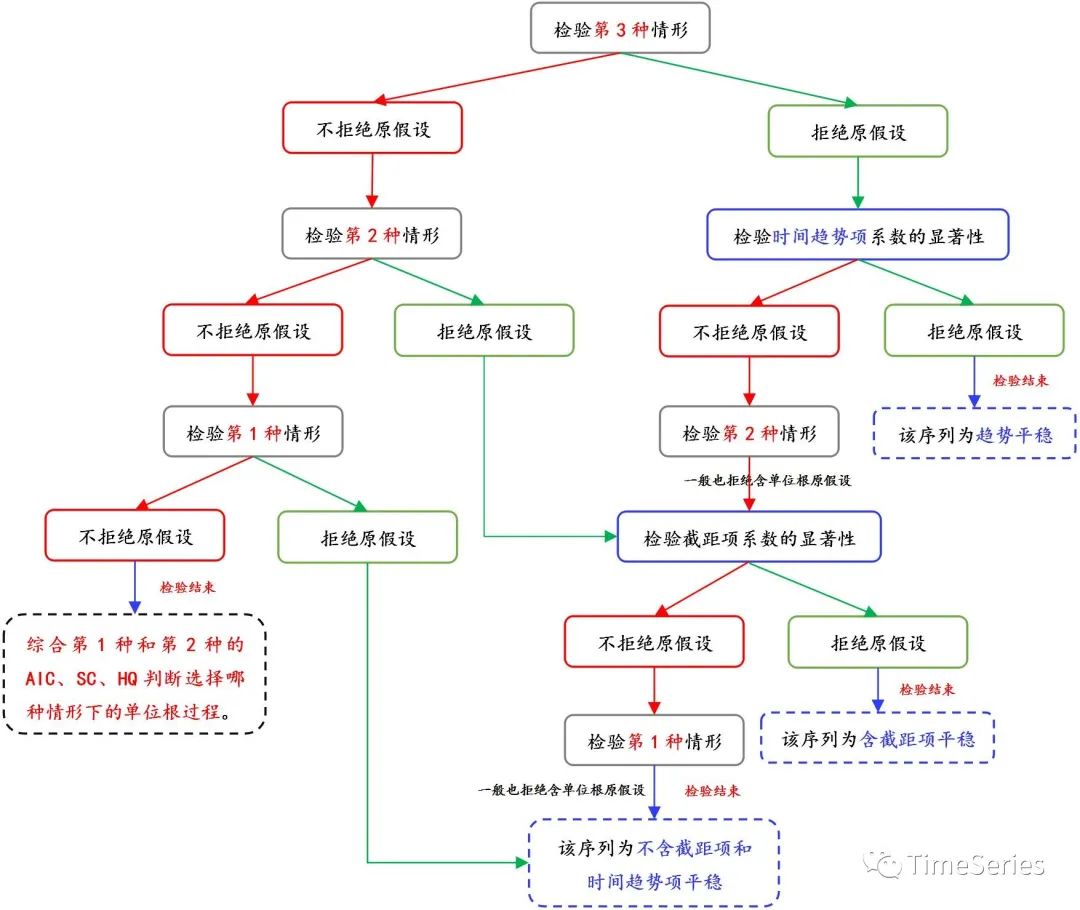
下图是网络中看到的单位根检验流程图以供参考(根据该流程可以确定序列是何种类型下的平稳,即便非平稳也可知道是何种类型下的非平稳序列):
ADF检验
DF的检验公式为一阶自回归过程,为了能适用于高阶自回归过程的平稳性检验,迪基等1984年对DF检验进行了一定的修正,引入了更高阶的滞后项,ADF的检验回归式修正为:

假设条件不变:
原假设 (存在单位根,时间序列是非平稳的) 备择假设 (不存在单位根,时间序列是平稳的--不含截距项和趋势项平稳/含截距项平稳/含截距项和趋势平稳)
检验流程同DF检验一致。若要严格判断序列是否是宽平稳的,可以直接检验是否不含截距项和趋势项平稳;若不能拒绝原假设(如p>0.05),序列非平稳,其实仍有必要检验序列是否是趋势平稳的。非平稳且非趋势平稳,可以使用一阶差分等平稳化方法处理后再做检验,若是趋势平稳,困于过度差分则不宜使用差分方式平稳化。
生成一个趋势平稳序列:
import numpy as np
from matplotlib import pyplot as plt
np.random.seed(123)
y = np.random.standard_normal(size=100)
for i in range(1, len(y)):
y[i] = 1 + 0.1*i + y[i]
plt.figure(figsize=(12, 6))
plt.plot(y)
plt.show()
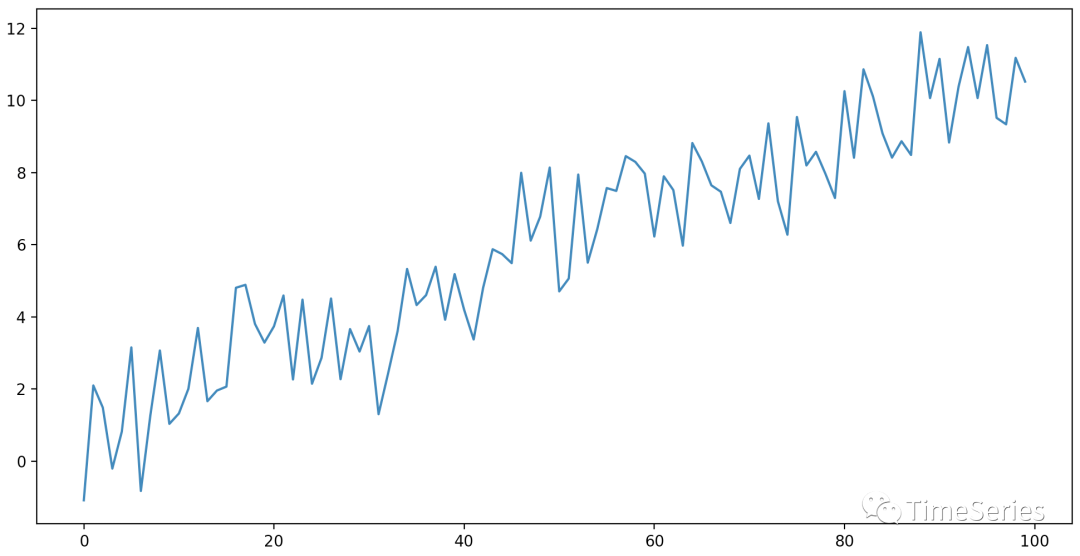
检验是否平稳:
from arch.unitroot import ADF
adf = ADF(y)
# print(adf.pvalue)
print(adf.summary().as_text())
adf = ADF(y)
adf.trend = 'ct'
print(adf.summary().as_text())

说明:
arch包中ADF检验可指定trend为
'n'(不含截距项和时间趋势项)
'c'(含截距项)
'ct'(含截距项和时间趋势项)
'ctt'(含截距项和时间趋势项和二次型时间趋势项)
分别对应不同平稳类型的检验。(滞后期lags默认为AIC最小)
以上第一个文本输出中,不指定trend默认为检验是否含截距项平稳,显著性水平p=0.836>0.05,不拒绝原假设,非平稳;
以上第二个文本输出中,指定trend为检验是否含截距项和时间趋势项平稳,显著性水平p=0.000<0.05,拒绝原假设,故为趋势项平稳。
我们再来看看GDP季节差分前后数据是否为平稳的:
# 数据在第一个代码块中
from arch.unitroot import ADF
adf = ADF(gdp)
print(adf.summary().as_text())
adf = ADF(gdp_diff)
print(adf.summary().as_text())

可以看到差分前p值为0.998>0.05,不能拒绝原假设,数据非平稳;差分后p值为0.003<0.05,故在5%的显著性水平下可拒绝原假设,差分后的数据是平稳的。
# 数据在第一个代码块中
from arch.unitroot import ADF
adf = ADF(gdp)
adf.trend = 'ct'
print(adf.summary().as_text())

指定检验平稳类型为含截距项和时间趋势项平稳,p值为0.693>0.05,同样不能拒绝原假设,故差分前亦非趋势平稳。
PP检验
Phillips和Perron(1988) 提出一种非参数检验方法,主要是为了解决残差项中潜在的序列相关和异方差问题,其检验统计量的渐进分布和临界值与 ADF检验相同。同样出现较早,假设条件一样,用法相似,可作为ADF检验的补充。
原假设 (存在单位根,时间序列是非平稳的) 备择假设 (不存在单位根,时间序列是平稳的--不含截距项和趋势项平稳/含截距项平稳/含截距项和趋势平稳)
同样构造一个趋势平稳序列,看下PP检验结果:
import numpy as np
from arch.unitroot import PhillipsPerron
np.random.seed(123)
y = np.random.standard_normal(size=100)
for i in range(1, len(y)):
y[i] = 1 + 0.1*i + y[i]
pp = PhillipsPerron(y)
print(pp.summary().as_text())
pp = PhillipsPerron(y)
pp.trend = 'ct'
print(pp.summary().as_text())

不指定trend为默认检验是否为带截距项的平稳过程,检验结果p值为0.055>0.05,对应检验统计量为-2.825大于5%显著性水平下的临界值-2.89,所以5%显著性水平下不拒绝原假设,为非平稳序列;但是检验统计量小于10%显著性水平下的临界值-2.58,故在10%的显著性水平下可拒绝原假设,认为是平稳序列。
指定trend=‘ct’为检验是否为带截距项和时间趋势项的平稳过程,检验结果p值为0.000<0.05,故为趋势平稳;其实检验统计量为-10.009小于1%显著性水平下的临界值-4.05,所以即便在1%显著性水平下也是平稳的。
基于以上检验结果,可以判定序列是趋势平稳的。
DF-GLS检验
DF-GLS检验,是Elliott, Rothenberg, and Stock 1996年提出的一种单位根检验方法,全称Dickey-Fuller Test with GLS Detredding,即“使用广义最小二乘法去除趋势的检验”,是目前最有功效的单位根检验。
DF-GLS检验利用广义最小二乘法,首先对要检验的数据进行一次“准差分”,然后利用准差分的数据对原序列进行去除趋势处理,再利用ADF检验的模型形式对去除趋势后的数据进行单位根检验,但此时ADF检验模型中不再包含常数项或者时间趋势变量。
原假设:序列存在单位根(时间序列是非平稳的) 备择假设:序列不存在单位根(时间序列是平稳的或趋势平稳的)
同样构造一个趋势平稳序列看下检验效果:
import numpy as np
from arch.unitroot import DFGLS
np.random.seed(123)
y = np.random.standard_normal(size=100)
for i in range(1, len(y)):
y[i] = 1 + 0.1*i + y[i]
dfgls = DFGLS(y)
print(dfgls.summary().as_text())
dfgls = DFGLS(y)
dfgls.trend = 'ct'
print(dfgls.summary().as_text())

不指定trend情况下不能拒绝原假设,非平稳;指定trend='ct'时p值小于0.05,拒绝原假设,带截距项和时间趋势平稳。
再来构造一个含单位根的非平稳序列看一下检验结果:
import numpy as np
from arch.unitroot import DFGLS
np.random.seed(123)
y = np.random.standard_normal(size=100)
for i in range(1, len(y)):
y[i] = 0.1 + y[i-1] + y[i]
dfgls = DFGLS(y)
print(dfgls.summary().as_text())
dfgls = DFGLS(y)
dfgls.trend = 'ct'
print(dfgls.summary().as_text())

p值一个为0.645,一个为0.347,均大于0.05/0.1。指不指定检验类型,均未能通过检验,故该序列为非平稳序列。(DF-GLS检验trend只能指定为'c'或者'ct')
KPSS检验
另一个著名的单位根存在的检验是Kwiatkowski, Phillips, and Shin 1992年提出的KPSS检验。与以上三种检验方法相比,最大的不同点就是它的原假设是平稳序列或趋势平稳序列,而备择假设是存在单位根。
原假设:序列不存在单位根(时间序列是平稳的或趋势平稳的) 备择假设:序列存在单位根(时间序列是非平稳的)
import numpy as np
from arch.unitroot import KPSS
np.random.seed(123)
y = np.random.standard_normal(size=100)
for i in range(1, len(y)):
y[i] = 0.1 + y[i-1] + y[i]
kpss = KPSS(y)
print(kpss.summary().as_text())
kpss = KPSS(y)
kpss.trend = 'ct'
print(kpss.summary().as_text())

注意KPSS检验中原假设为不存在单位根。默认检验趋势类型下p值为0.000,拒绝原假设,存在单位根,序列非平稳。指定trend='ct'后,p值0.115>0.05,不拒绝原假设,认为序列趋势平稳,检验错误。以上几种检验中均不能100%保证检验正确,PP检验可认为是ADF检验的补充,KPSS检验同样也可和其他检验一同使用,当均认为是平稳或趋势平稳时方判定为平稳。
除以上检验方法外,还有Zivot-Andrews检验、Variance Ratio检验等检验方法。
以上代码实现中使用的是Python中的arch包,另外还有一个常用的包statsmodels中也实现了单位根检验方法,结果是一样的。
| Method/Model | Package/Module (function/class) |
|---|---|
| Augmented Dickey-Fuller test | statsmodels.tsa.stattools (adfuller) arch.unitroot (ADF) |
| Phillip-Perron test | arch.unitroot (PhillipsPerron) |
| Dickey-Fuller GLS Test | arch.unitroot (DFGLS) |
| KPSS test | statsmodels.tsa.stattools (kpss) arch.unitroot (KPSS) |
| Zivot-Andrew test | statsmodels.tsa.stattools (zivot_andrews) arch.unitroot (ZivotAndrews) |
| Variance Ratio test | arch.unitroot (VarianceRatio) |
[1] http://course.sdu.edu.cn/G2S/eWebEditor/uploadfile/20140525165255371.pdf
[2] https://max.book118.com/html/2016/0518/43276093.shtm
[3] https://doc.mbalib.com/view/ef1783f2fa1892f6ad016281ed743d78.html
[4] https://www.stata.com/manuals13/tsdfgls.pdf
[5] https://zhuanlan.zhihu.com/p/50553021
[6] https://arch.readthedocs.io/en/latest/index.html

E N D

