搞定笔试!猿辅导2021笔试真题攻略(上)
共 2562字,需浏览 6分钟
·
2021-04-27 02:20
点击上方蓝字,关注并星标,和我一起学技术。
大家好,最近春招刚过,眼看着实习生招聘和暑期的招聘近在眼前,所以特地选了一些笔试题给大家做个简单的分享。希望可以帮助到有招聘需求的同学们取得好结果。
这次选择的题目是猿辅导今年的春招笔试题中的六道选择题,虽然是选择题,但我做了一下,这套题目挺有意思,难度也不低,挺有区分度的。
好了废话不多说,我们来看题吧。
第一题

这题言简意赅,很多信息都融合在了一句话里。有几个重点,首先是有序,其次是链表,最后是合并。也就是说这是一个N个有序链表的合并问题。
那有序链表如何合并呢?其实如果大家对归并排序熟悉的话,其实归并排序中的合并部分就可以看做是有序链表合并。所以我们只需要根据归并排序复杂度的计算方式来计算即可,那归并排序的复杂度又是如何计算的呢?我们可以先来看图,着重看下下图当中合并的部分。
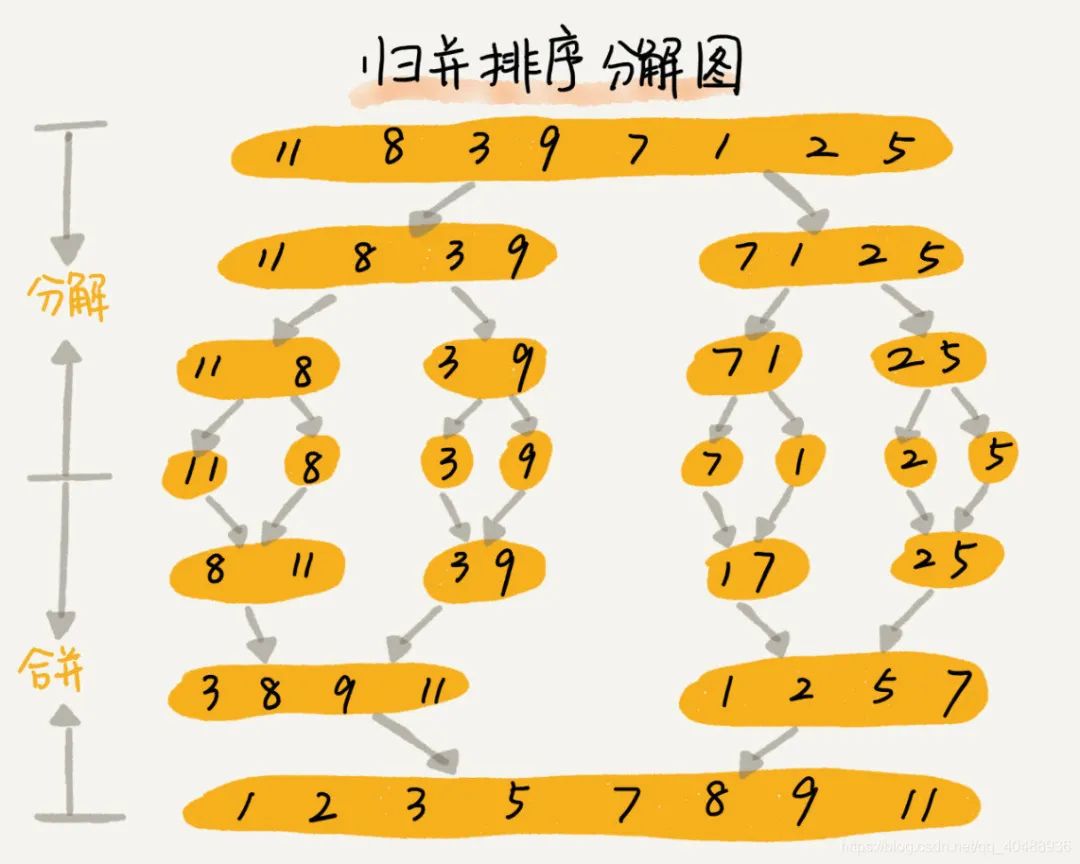
归并排序的合并部分其实可以等价看成是N个长度为1的有序链表的合并,我们先纵向看,每次合并都可以将待归并的链表的数量减少一半。因为一共有N个链表,所以一共需要次归并才能得到一个完整的链表。接着我们再横向来看,每次归并的时候,我们都需要把这些链表遍历一遍,虽然链表的数量是一个变量,但是遍历的元素总和是确定的,也就是所有元素的数量,在这道题当中元素的数量是N x M。
所以最后我们把每一层遍历的元素数量乘上层数,得到的就是最终的复杂度了,所以答案是,所以应该选A。
第二题

题目比较仁慈问的是4个节点组成的二叉树的数量,所以还是可以通过纸上一个一个罗列来计算的,但如果问的是5个或者是6个节点,就很难通过罗列得到了。
其实这题我们有数学的方法来解决,我们假设f(n)代表n个节点组成的二叉树的种数。显然f(0) = 1, f(1) = 1, f(2) = 2,只要我们能写出f这个函数的通项公式或者是递推式,我们就可以推算出来每一个f的值。显然相比于通项公式,递推式来的更简单一些。
怎么递推呢?其实很简单,二叉树是可以拆分的,我们可以按照根节点将它分成左边部分以及右边部分。我们假设左边部分一共有k个节点,那么通过计算可以得到右边部分一共有n-1-k个节点。这样我们只要枚举所有的k,就可以得到f(n)。
表达式也就不难写出了:。
通过这个式子不难算出f(4) = 14,故选B。
第三题

根据题目中的描述我们可以知道,小明和小红出现在车站等车的时间段是一样的,他们两人能相遇只有他们都在等车的时候。其中小明的车次更多,每五分钟一班,我们画出时间轴,将九点到十点这个时间段内可以分成12段。如果我们把小明等车的时刻看成是一个点的话,那么这个点落在其中每一段当中的概率都是一样的,都是1/12。
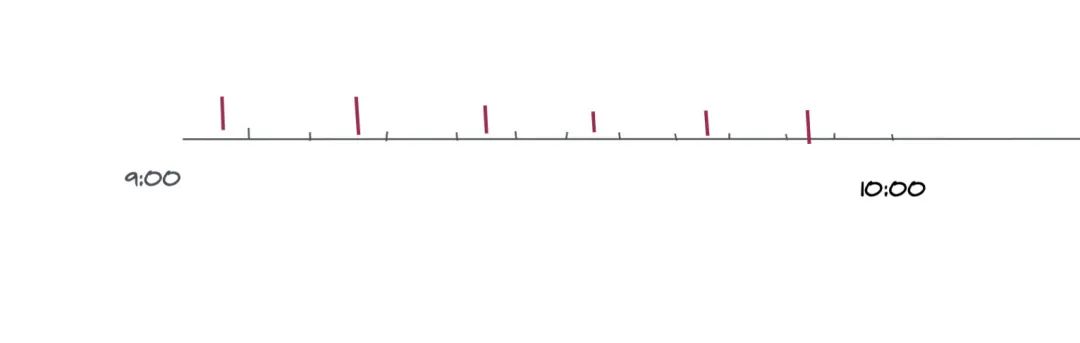
剩下的我们就只需要考虑小红,这个时候有两种情况,第一种情况就是小红也落在同样的时间段内,那么他们两人相遇。第二种情况是由于小红的车次等待的时间更长,小红额外多等了一个区间和小明相遇。对于第一种情况很好算,概率就是1/12,对于第二种情况其实也不复杂。我们观察一下可以发现,小红只有出现在上图当中标了红线的区间内才有可能额外多等5分钟。对于这种情况,它的概率是小红出现在标红的格子中的概率1/2,乘上小明出现在标红格子之后的格子里的概率1/12。
所以最终的答案是1/12 + 1/2 * 1/12 = 3/24 = 1/8,选A。
第四题

这题很简单,就是一个简单的条件概率,我们把发现一个bug看成是事件B,小明写出bug为事件A,根据贝叶斯公式可以写出:
所以本题选A。
第五题

第五题同样是条件概率。
我们简单肉眼评估一下就可以排除掉前面两个选项,所以正确答案就在C和D当中。同样简单算一下就可以发现C不对,因为准时到是坐地铁还是骑自行车来的概率是一个条件概率,不能通过简单的0.3 + 0.2进行计算,所以多半是错的。通过排除法也可以确定答案D是正确选项。
当然我们要进行验证也不难,我们把骑电动车看成事件A,准时到看成事件B。那么骑电动车准时到的概率就是,简单评估一下也可以看出来它大于0.5。
第六题

这题乍一看比较难算,因为语文书和数学书都有两本, 它们都有可能相邻,并且既可能只相邻一个也可能两个同时相邻。所以需要我们理清思路一点点计算,首先,5本书各不相同,它的全排列是5! = 120种。
其次考虑相邻,相邻一共有三种情况,分别是语文书相邻但数学书不相邻,以及数学书相邻语文书不相邻,以及它们都相邻。对于前两种情况来说是一样的,我们计算其中一种乘二即可,第三种情况也很好算,我们只需要把语文书和数学书捆绑看成是一本即可。
对于语文书相邻数学书不相邻的情况,我们可以先把两本语文书捆绑看成是一体,之后强行给数学书分开。数学书要分开只有三种情况,第一种是中间隔着一本英语书,第二种是中间隔着两本语文书,第三种是两本语文和一本英语都夹在中间。我们先来看中间隔着英语书的情况,我们把数学书和英语书捆绑之后,可以看成是数学书和语文书的排列,即种,再加上语文书本身有两种排列,和数学书的两种排列,相乘是8种。同理,两本数学书中间隔着两本语文书的情况一共也有4种,再加上和英语书的排列,一共也是8种。最后一种情况是两本数学书在最外侧,把其他所有书都包含在内,不难算出这种情况也一共有8种。以上的情况全部相加一共有24种,与之对应的数学书相邻语文书不相邻的情况同样也就是24种。
最后我们再来看语文和数学都相邻的情况,我们一样可以采用打包策略,把语文书和数学书都分别打包看成一个整体。这样的话全排列是3 * 2 * 1 = 6种,再乘上打包的4种情况,也就是一共也是24种。
所以最终的答案就是,这里得多说一句牛客网里这道题给的答案有误,大家做题的时候注意一下。
总结
这题猿辅导的题目一共有14题,由于题量不小,我做了一些拆分没有放在一篇文章当中。大家对原题感兴趣想要亲自试验的话可以点击阅读原文进行跳转,剩余的题目会在之后的文章当中继续分享。
今天的文章就到这里,感谢大家的阅读,喜欢的话不要忘了三连和星标。
