搜索

头条高级面试题：请谈谈Redis 9种数据结构以及它们的内部编码实现

Java技术驿站

共 12845字，需浏览 26分钟

 ·

2021-08-30 04:56

90%的人知道Redis 5种最基本的数据结构，只有不到10%的人知道8种基本数据结构（5种基本+bitmap+GeoHash+HyperLogLog），只有不到5%的人知道9种基本数据结构（5.0最新版本数据结构Streams），只有不到1%的人掌握了所有9种基本数据结构以及8种内部编码，掌握这篇文章的知识点，让你成为面试官眼中Redis方面最靓的仔！

说明：本文基于Redis-3.2.11版本源码进行分析。

5种普通数据结构

这个没什么好说的，对Redis稍微有点了解的都知道5种最基本的数据结构：String，List，Hash，Set，Sorted Set。不过，需要注意的是，这里依然有几个高频面试题。

  • Set和Hash的关系

答案就是Set是一个特殊的value为空的Hash。Set类型操作的源码在t_set.c中。以新增一个元素为例（int setTypeAdd(robj *subject, sds value)），如果编码类型是OBJ_ENCODING_HT，那么新增源码的源码如下，事实上就是对dict即Hash数据结构进行操作，并且dictSetVal时value是NULL：

dictEntry *de = dictAddRaw(ht,value,NULL);
if (de) {
    dictSetKey(ht,de,sdsdup(value));
    dictSetVal(ht,de,NULL);
    return 1;
}

同样的，我们在t_hash.c中看到Hash类型新增元素时，当判断编码类型是OBJ_ENCODING_HT时，也是调用dict的方法：dictAdd(o->ptr,f,v)，dictAdd最终也是调用dictSetVal()方法，只不过v即value不为NULL：

/* Add an element to the target hash table */
int dictAdd(dict *d, void *key, void *val)
{
    dictEntry *entry = dictAddRaw(d,key,NULL);

    if (!entry) return DICT_ERR;
    dictSetVal(d, entry, val);
    return DICT_OK;
}

所以，Redis中Set和Hash的关系就很清楚了，当编码是OBJ_ENCODING_HT时，两者都是dict数据类型，只不过Set是value为NULL的特殊的dict。

  • 谈谈你对Sorted Set的理解

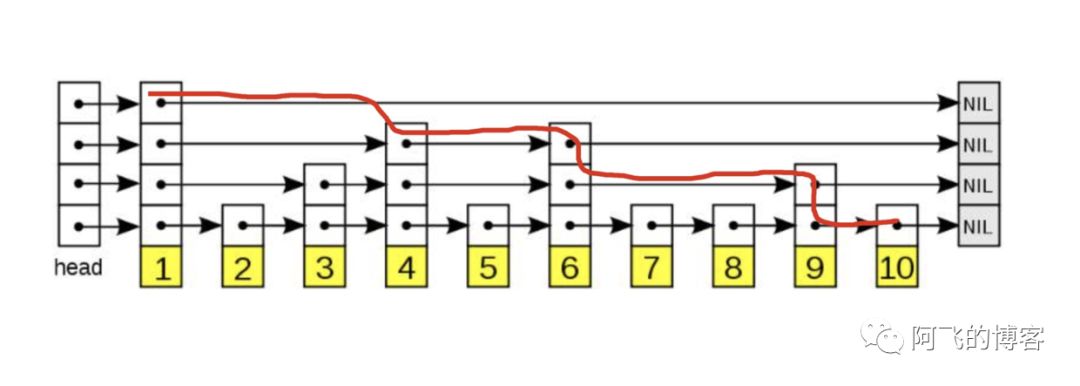
Sorted Set的数据结构是一种跳表，即SkipList，如下图所示，红线是查找10的过程：

SkipList

  • 如何借助Sorted set实现多维排序

Sorted Set默认情况下只能根据一个因子score进行排序。如此一来，局限性就很大，举个栗子：热门排行榜需要按照下载量&最近更新时间排序，即类似数据库中的ORDER BY download_count, update_time DESC。那这样的需求如果用Redis的Sorted Set实现呢？

事实上很简单，思路就是将涉及排序的多个维度的列通过一定的方式转换成一个特殊的列，即result = function(x, y, z)，即x，y，z是三个排序因子，例如下载量、时间等，通过自定义函数function()计算得到result，将result作为Sorted Set中的score的值，就能实现任意维度的排序需求了。可以参考笔者之前的文章：《Redis高级玩法：如何利用SortedSet实现多维度排序》。

Redis内部编码

我们常说的String，List，Hash，Set，Sorted Set只是对外的编码，实际上每种数据结构都有自己底层的内部编码实现，而且是多种实现，这样Redis可以在合适的场景选择更合适的内部编码。

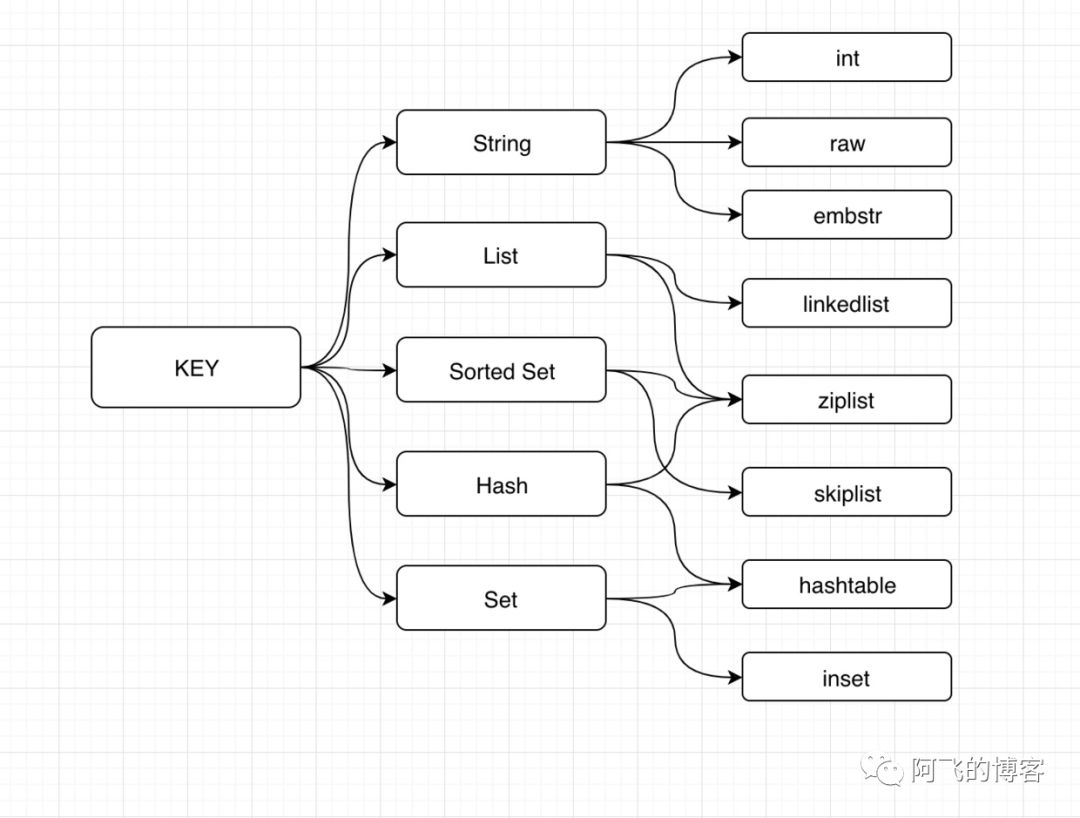
如下图所示（图片纠正：intset编码，而不是inset编码），可以看到每种数据结构都有2种以上的内部编码实现，例如String数据结构就包含了raw、int和embstr三种内部编码。同时，有些内部编码可以作为多种外部数据结构的内部实现，例如ziplist就是hash、list和zset共有的内部编码，而set的内部编码可能是hashtable或者intset：

Redis内部编码

Redis这样设计有两个好处：

  1. 可以偷偷的改进内部编码，而对外的数据结构和命令没有影响，这样一旦开发出更优秀的内部编码，无需改动对外数据结构和命令。

  2. 多种内部编码实现可以在不同场景下发挥各自的优势。例如ziplist比较节省内存，但是在列表元素比较多的情况下，性能会有所下降。这时候Redis会根据配置选项将列表类型的内部实现转换为linkedlist。

String的3种内部编码

由上图可知，String的3种内部编码分别是：int、embstr、raw。int类型很好理解，当一个key的value是整型时，Redis就将其编码为int类型（另外还有一个条件：把这个value当作字符串来看，它的长度不能超过20）。如下所示。这种编码类型为了节省内存。Redis默认会缓存10000个整型值（#define OBJ_SHARED_INTEGERS 10000），这就意味着，如果有10个不同的KEY，其value都是10000以内的值，事实上全部都是共享同一个对象：

127.0.0.1:6379> set number "7890"
OK
127.0.0.1:6379> object encoding number
"int"

接下来就是ebmstr和raw两种内部编码的长度界限，请看下面的源码：

#define OBJ_ENCODING_EMBSTR_SIZE_LIMIT 44
robj *createStringObject(const char *ptr, size_t len) {
    if (len <= OBJ_ENCODING_EMBSTR_SIZE_LIMIT)
        return createEmbeddedStringObject(ptr,len);
    else
        return createRawStringObject(ptr,len);
}

也就是说，embstr和raw编码的长度界限是44，我们可以做如下验证。长度超过44以后，就是raw编码类型，不会有任何优化，是多长，就要消耗多少内存：

127.0.0.1:6379> set name "a1234567890123456789012345678901234567890123"
OK
127.0.0.1:6379> object encoding name
"embstr"
127.0.0.1:6379> set name "a12345678901234567890123456789012345678901234"
OK
127.0.0.1:6379> object encoding name
"raw"

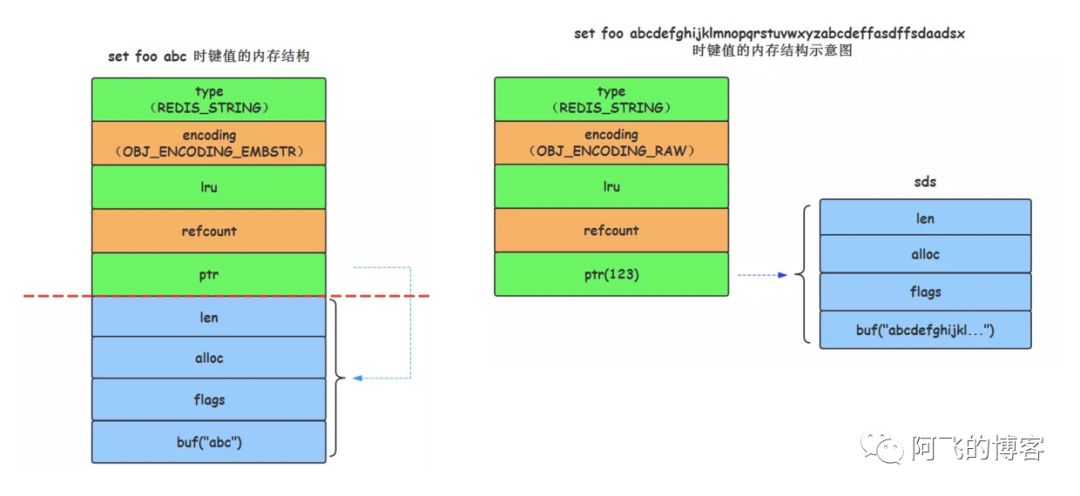
那么为什么有embstr编码呢？它相比raw的优势在哪里？embstr编码将创建字符串对象所需的空间分配的次数从raw编码的两次降低为一次。因为embstr编码的字符串对象的所有数据都保存在一块连续的内存里面，所以这种编码的字符串对象比起raw编码的字符串对象能更好地利用缓存带来的优势。并且释放embstr编码的字符串对象只需要调用一次内存释放函数，而释放raw编码对象的字符串对象需要调用两次内存释放函数。如下图所示，左边是embstr编码，右边是raw编码：

embstr V.S. raw

ziplist

由前面的图可知，List，Hash，Sorted Set三种对外结构，在特殊情况下的内部编码都是ziplist，那么这个ziplist有什么神奇之处呢？

以Hash为例，我们首先看一下什么条件下它的内部编码是ziplist：

  1. 当哈希类型元素个数小于hash-max-ziplist-entries配置（默认512个）；

  2. 所有值都小于hash-max-ziplist-value配置（默认64个字节）；

如果是sorted set的话，同样需要满足两个条件：

  1. 元素个数小于zset-max-ziplist-entries配置，默认128；

  2. 所有值都小于zset-max-ziplist-value配置，默认64。

实际上，ziplist充分体现了Redis对于存储效率的追求。一个普通的双向链表，链表中每一项都占用独立的一块内存，各项之间用地址指针（或引用）连接起来。这种方式会带来大量的内存碎片，而且地址指针也会占用额外的内存。而ziplist却是将表中每一项存放在前后连续的地址空间内，一个ziplist整体占用一大块内存。它是一个表（list），但其实不是一个链表（linked list）。

ziplist的源码在ziplist.c这个文件中，其中有一段这样的描述 -- The general layout of the ziplist is as follows:：

<zlbytes> <zltail> <zllen> <entry> <entry> ... <entry> <zlend>

  • zlbytes：表示这个ziplist占用了多少空间，或者说占了多少字节，这其中包括了zlbytes本身占用的4个字节；

  • zltail：表示到ziplist中最后一个元素的偏移量，有了这个值，pop操作的时间复杂度就是O(1)了，即不需要遍历整个ziplist；

  • zllen：表示ziplist中有多少个entry，即保存了多少个元素。由于这个字段占用16个字节，所以最大值是2^16-1，也就意味着，如果entry的数量超过2^16-1时，需要遍历整个ziplist才知道entry的数量；

  • entry：真正保存的数据，有它自己的编码；

  • zlend：专门用来表示ziplist尾部的特殊字符，占用8个字节，值固定为255，即8个字节每一位都是1。

如下就是一个真实的ziplist编码，包含了2和5两个元素：

 [0f 00 00 00] [0c 00 00 00] [02 00] [00 f3] [02 f6] [ff]
       |             |          |       |       |     |
    zlbytes        zltail    entries   "2"     "5"   end

linkedlist

这是List的一种编码数据结构非常简单，就是我们非常熟悉的双向链表，对应Java中的LinkedList。

skiplist

这个前面也已经提及，就是经典的跳表数据结构。

hashtable

这个也很容易，对应Java中的HashMap。

intset

Set特殊内部编码，当满足下面的条件时Set的内部编码就是intset而不是hashtable：

  1. Set集合中必须是64位有符号的十进制整型；

  2. 元素个数不能超过set-max-intset-entries配置，默认512；

验证如下：

127.0.0.1:6379> sadd scores 135
(integer) 0
127.0.0.1:6379> sadd scores 128
(integer) 1
127.0.0.1:6379> object encoding scores
"intset"

那么intset编码到底是个什么东西呢？看它的源码定义如下，很明显，就是整型数组，并且是一个有序的整型数组。它在内存分配上与ziplist有些类似，是连续的一整块内存空间，而且对于大整数和小整数采取了不同的编码，尽量对内存的使用进行了优化。这样的数据结构，如果执行SISMEMBER命令，即查看某个元素是否在集合中时，事实上使用的是二分查找法：

typedef struct intset {
    uint32_t encoding;
    uint32_t length;
    int8_t contents[];
} intset;

// intset编码查找方法源码（人为简化），标准的二分查找法：
static uint8_t intsetSearch(intset *is, int64_t value, uint32_t *pos) {
    int min = 0, max = intrev32ifbe(is->length)-1, mid = -1;
    int64_t cur = -1;

    while(max >= min) {
        mid = ((unsigned int)min + (unsigned int)max) >> 1;
        cur = _intsetGet(is,mid);
        if (value > cur) {
            min = mid+1;
        } else if (value < cur) {
            max = mid-1;
        } else {
            break;
        }
    }

    if (value == cur) {
        if (pos) *pos = mid;
        return 1;
    } else {
        if (pos) *pos = min;
        return 0;
    }
}

#define INTSET_ENC_INT16 (sizeof(int16_t))
#define INTSET_ENC_INT32 (sizeof(int32_t))
#define INTSET_ENC_INT64 (sizeof(int64_t))


3种高级数据结构

Redis中3种高级数据结构分别是bitmap、GEO、HyperLogLog，针对这3种数据结构，笔者之前也有文章介绍过。其中，最重要的就是bitmap。

bitmap

这个就是Redis实现的BloomFilter，BloomFilter非常简单，如下图所示，假设已经有3个元素a、b和c，分别通过3个hash算法h1()、h2()和h2()计算然后对一个bit进行赋值，接下来假设需要判断d是否已经存在，那么也需要使用3个hash算法h1()、h2()和h2()对d进行计算，然后得到3个bit的值，恰好这3个bit的值为1，这就能够说明：d可能存在集合中。再判断e，由于h1(e)算出来的bit之前的值是0，那么说明：e一定不存在集合中：

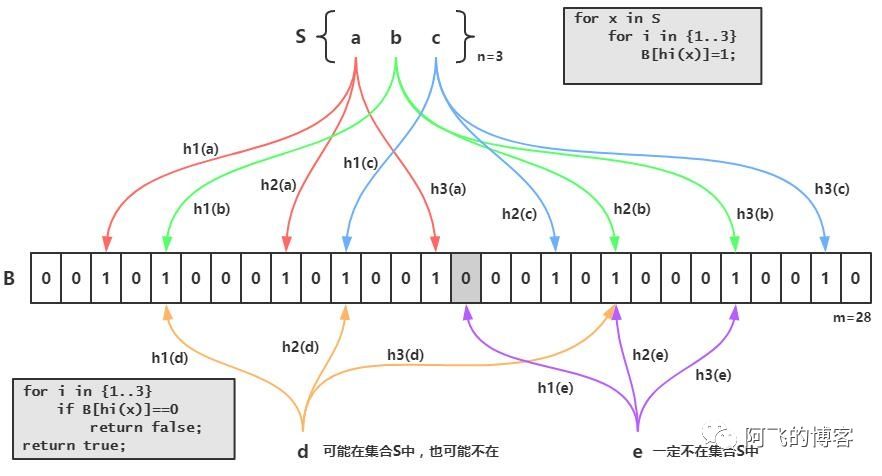
BloomFilter

需要说明的是，bitmap并不是一种真实的数据结构，它本质上是String数据结构，只不过操作的粒度变成了位，即bit。因为String类型最大长度为512MB，所以bitmap最多可以存储2^32个bit。

GEO

GEO数据结构可以在Redis中存储地理坐标，并且坐标有限制，由EPSG:900913 / EPSG:3785 / OSGEO:41001 规定如下：

  1. 有效的经度从-180度到180度。

  2. 有效的纬度从-85.05112878度到85.05112878度。

当坐标位置超出上述指定范围时，该命令将会返回一个错误。添加地理位置命令如下：

redis> GEOADD city 114.031040 22.324386 "shenzhen" 112.572154 22.267832 "guangzhou"
(integer) 2
redis> GEODIST city shenzhen guangzhou
"150265.8106"

但是，需要说明的是，Geo本身不是一种数据结构，它本质上还是借助于Sorted Set（ZSET），并且使用GeoHash技术进行填充。Redis中将经纬度使用52位的整数进行编码，放进zset中，score就是GeoHash的52位整数值。在使用Redis进行Geo查询时，其内部对应的操作其实就是zset(skiplist)的操作。通过zset的score进行排序就可以得到坐标附近的其它元素，通过将score还原成坐标值就可以得到元素的原始坐标。

总之，Redis中处理这些地理位置坐标点的思想是：二维平面坐标点 --> 一维整数编码值 --> zset(score为编码值) --> zrangebyrank(获取score相近的元素)、zrangebyscore --> 通过score(整数编码值)反解坐标点 --> 附近点的地理位置坐标。

  • GEOHASH原理

使用wiki上的例子，纬度为42.6，经度为-5.6的点，转化为base32的话要如何转呢？
首先拿纬度来进行说明，纬度的范围为-90到90，将这个范围划为两段，则为[-90,0]、[0,90]，然后看给定的纬度在哪个范围，在前面的范围的话，就设当前位为0，后面的话值便为1.然后继续将确定的范围1分为2，继续以确定值在前段还是后段来确定bit的值。就这样慢慢的缩小范围，一般最多缩小13次就可以了(经纬度的二进制位相加最多25位，经度13位，纬度12位)。这时的中间值，将跟给定的值最相近。如下图所示：

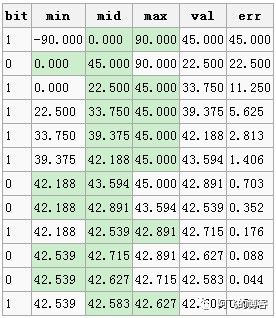
Geohash

第1行，纬度42.6位于[0, 90]之间，所以bit=1；第2行，纬度42.6位于[0, 45]之间，所以bit=0；第3行，纬度42.6位于[22.5, 45]之间，所以bit=1，以此类推。这样，取出图中的bit位：1011 1100 1001，同样的方法，将经度(范围-180到180)算出来为 ：0111 1100 0000 0。结果对其如下：

# 经度
0111 1100 0000 0
# 纬度
1011 1100 1001

得到了经纬度的二进制位后，下面需要将两者进行结合：从经度、纬度的循环，每次取其二进制的一位(不足位取0)，合并为新的二进制数：01101111 11110000 01000001 0。每5位为一个十进制数，结合base32对应表映射为base32值为：ezs42。这样就完成了encode的过程。

Streams

这是Redis5.0引入的全新数据结构，这种数据结构笔者之前也有文章对其进行详细解读，链接地址：《Streams：深入剖析Redis5.0全新数据结构》，用一句话概括Streams就是Redis实现的内存版kafka。而且，Streams也有Consumer Groups的概念。通过Redis源码中对stream的定义我们可知，streams底层的数据结构是radix tree：

typedef struct stream {
    rax *rax;               /* The radix tree holding the stream. */
    uint64_t length;        /* Number of elements inside this stream. */
    streamID last_id;       /* Zero if there are yet no items. */
    rax *cgroups;           /* Consumer groups dictionary: name -> streamCG */
} stream;

那么这个radix tree长啥样呢？在Redis源码的rax.h文件中有一段这样的描述，这样看起来是不是就比较直观了：

 *                    (f) ""
 *                    /
 *                 (i o) "f"
 *                 /   \
 *    "firs"  ("rst")  (o) "fo"
 *              /        \
 *    "first" []       [t   b] "foo"
 *                     /     \
 *           "foot" ("er")    ("ar") "foob"
 *                    /          \
 *          "footer" []          [] "foobar"

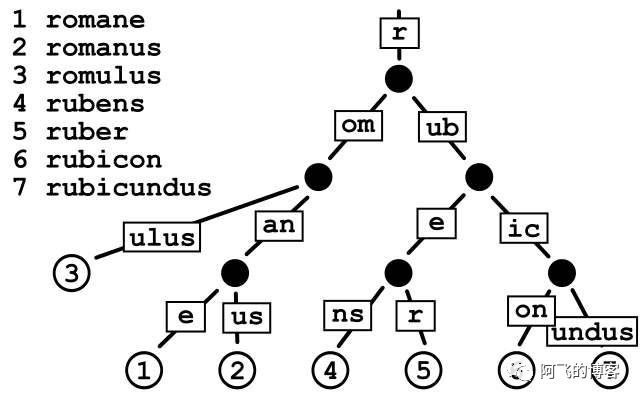
Radix Tree(基数树) 事实上就几乎相同是传统的二叉树。仅仅是在寻找方式上，以一个unsigned int类型数为例，利用这个数的每个比特位作为树节点的推断。能够这样说，比方一个数10001010101010110101010，那么依照Radix 树的插入就是在根节点，假设遇到0，就指向左节点，假设遇到1就指向右节点，在插入过程中构造树节点，在删除过程中删除树节点。如下是一个保存了7个单词的Radix Tree：

radix tree



浏览 20
点赞
评论
收藏
分享

手机扫一扫分享

分享
举报
评论
图片
表情
推荐
面试官：Redis数据结构与内部编码，你知道多少？
码农沉思录
0
Redis 数据结构与对象编码 (Object Encoding)
java1234
0
图解 Redis 五种数据结构底层实现
武培轩
0
Redis的常用淘汰策略以及算法实现
java1234
0
Redis面试题!
python爬虫人工智能大数据
0
【面试题】2055- 谈谈前端路由的实现原理【hash＆history】
前端自习课
0
面试题：Redis如何实现分布式锁！
月伴飞鱼
0
springboot整合redis以及实现分布式锁
java1234
0
Redis 数据结构扩展
JAVA乐园
0
面试官：请你谈谈用Redis实现一个轻量级的搜索引擎！
Java技术迷
0
点赞
评论
收藏
分享

手机扫一扫分享

分享
举报