Python时间序列分析--ARIMA模型实战案例
共 2939字,需浏览 6分钟
·
2021-11-12 15:23
本文将介绍使用Python来完成时间序列分析ARIMA模型的完整步骤与流程,绘制时序图,平稳性检验,单位根检验,白噪声检验,模型定阶,模型有啊,参数估计,模型检验等完整步骤。Python建立时间序列分析–ARIMA模型实战案例
时间序列分析概念

时间序列分析 是统计学中的一个非常重要的分支,是以概率论与数理统计为基础、计算机应用为技术支撑,迅速发展起来的一种应用性很强的科学方法。时间序列是变量按时间间隔的顺序而下形成的随机变量序列,大量自然界、社会经济等领域的统计指标都依年、季、月或日统计其指标值,随着时间的推移,形成了统计指标的时间序列,例如,股价指数、物价指数、GDP和产品销售量等等都属于时间序列。原文链接:https://blog.csdn.net/qq_45176548/article/details/111504846
建立模型基本步骤
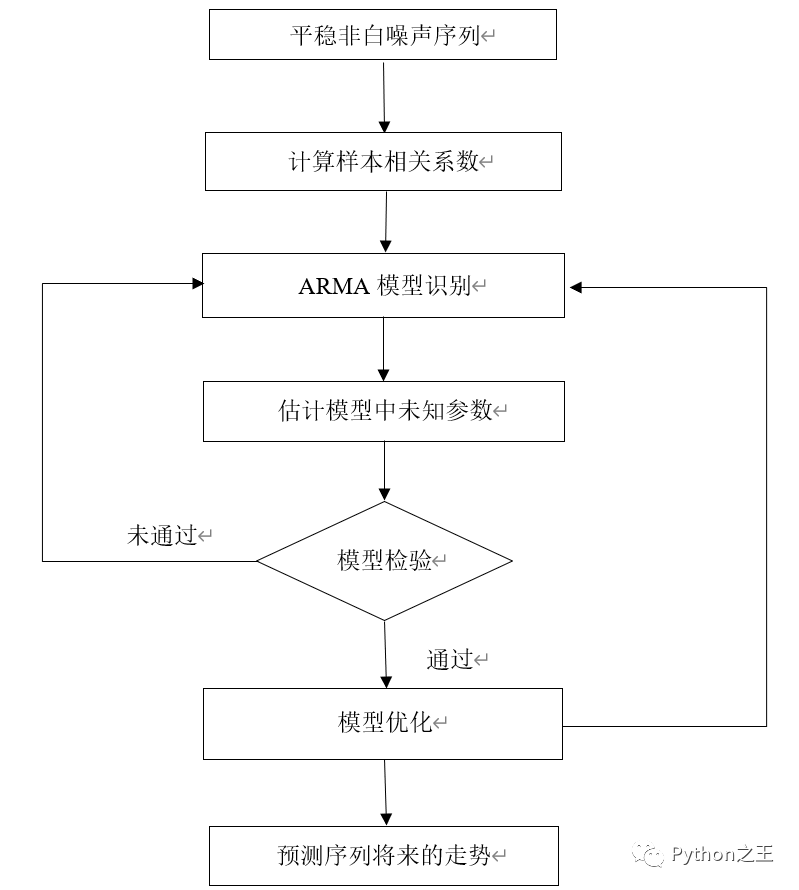
ARIMA模型建模实战
导入模块
import sys
import os
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
from arch.unitroot import ADF
import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import style
style.use('ggplot')
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.api import qqplot
pd.set_option('display.float_format', lambda x: '%.5f' % x)
np.set_printoptions(precision=5, suppress=True)
"""中文显示问题"""
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
加载数据
data = pd.read_excel("data.xlsx",index_col="年份",parse_dates=True)
data.head()
| 年份 |
|---|
| 1952-01-01 |
| 1953-01-01 |
| 1954-01-01 |
| 1955-01-01 |
| 1956-01-01 |
平稳性检验
时序图
data["diff1"] = data["xt"].diff(1).dropna()
data["diff2"] = data["diff1"].diff(1).dropna()
data1 = data.loc[:,["xt","diff1","diff2"]]
data1.plot(subplots=True, figsize=(18, 12),title="差分图")
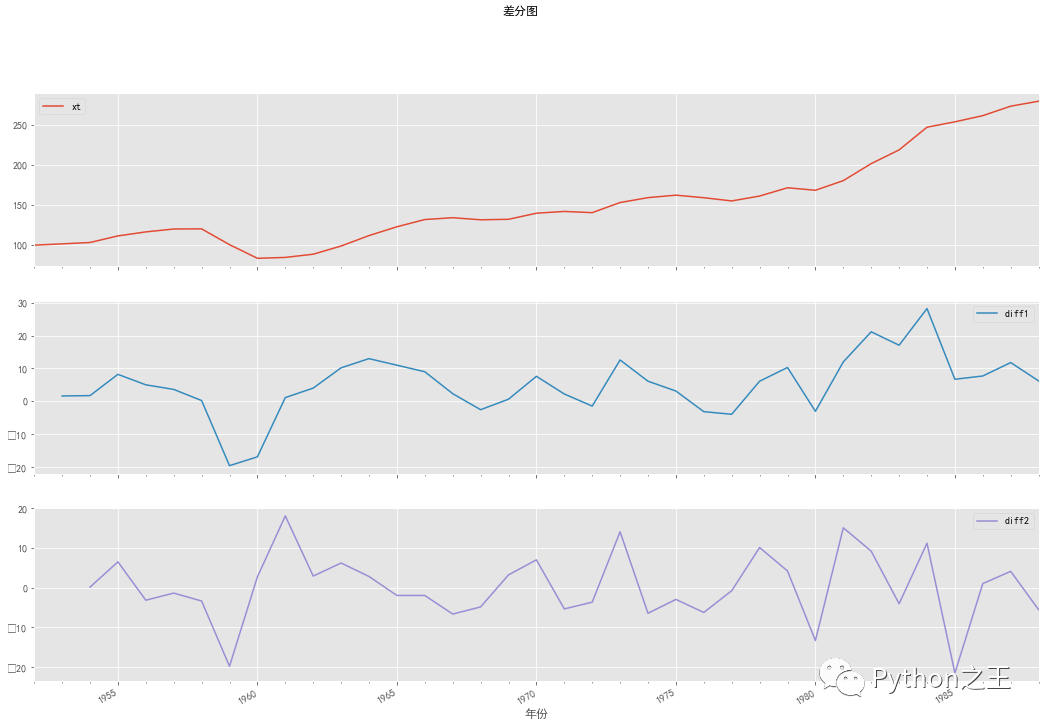
时序图检验 - - 全靠肉眼的判断和判断人的经验,不同的人看到同样的图形,很可能会给出不同的判断。因此我们需要一个更有说服力、更加客观的统计方法来帮助我们检验时间序列的平稳性,这种方法,就是单位根检验。原文链接:https://blog.csdn.net/qq_45176548/article/details/111504846
单位根检验
print("单位根检验:\n")
print(ADF(data.diff1.dropna()))
单位根检验:
Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.156
P-value 0.023
Lags 0
-------------------------------------
Trend: Constant
Critical Values: -3.63 (1%), -2.95 (5%), -2.61 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
单位根检验:对其一阶差分进行单位根检验,得到:1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,本数据中,P-value 为 0.023,接近0,ADF Test result同时小于5%、10%即说明很好地拒绝该假设,本数据中,ADF结果为-3.156,拒绝原假设,即一阶差分后数据是平稳的。
白噪声检验
判断序列是否为非白噪声序列
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(data.diff1.dropna(), lags = [i for i in range(1,12)],boxpierce=True)
(array([11.30402, 13.03896, 13.37637, 14.24184, 14.6937 , 15.33042,
16.36099, 16.76433, 18.15565, 18.16275, 18.21663]),
array([0.00077, 0.00147, 0.00389, 0.00656, 0.01175, 0.01784, 0.02202,
0.03266, 0.03341, 0.05228, 0.07669]),
array([10.4116 , 11.96391, 12.25693, 12.98574, 13.35437, 13.85704,
14.64353, 14.94072, 15.92929, 15.93415, 15.9696 ]),
array([0.00125, 0.00252, 0.00655, 0.01135, 0.02027, 0.03127, 0.04085,
0.06031, 0.06837, 0.10153, 0.14226]))
通过P<α,拒绝原假设,故差分后的序列是平稳的非白噪声序列,可以进行下一步建模
模型定阶
现在我们已经得到一个平稳的时间序列,接来下就是选择合适的ARIMA模型,即ARIMA模型中合适的p,q。第一步我们要先检查平稳时间序列的自相关图和偏自相关图。通过sm.graphics.tsa.plot_acf和sm.graphics.tsa.plot_pacf得到图形
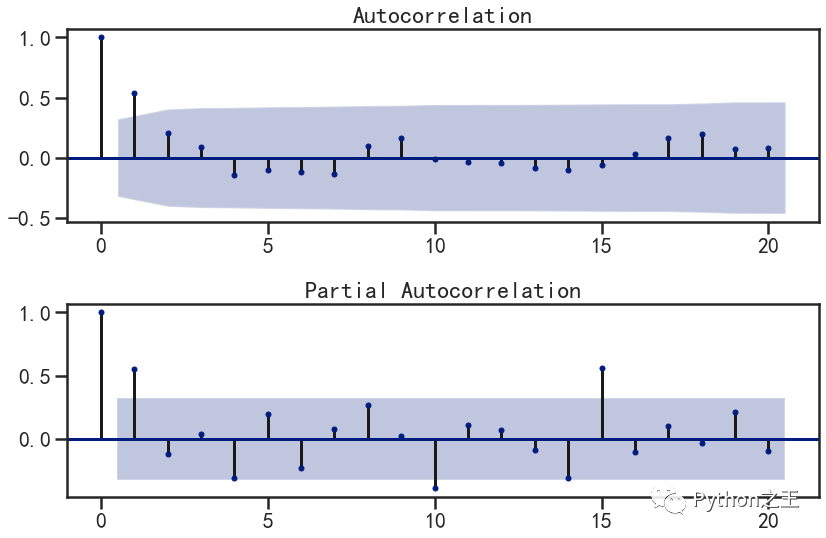
从一阶差分序列的自相关图和偏自相关图可以发现:
自相关图拖尾或一阶截尾1. 偏自相关图一阶截尾,- 所以我们可以建立ARIMA(1,1,0)、ARIMA(1,1,1)、ARIMA(0,1,1)模型。
模型优化

其中L是在该模型下的最大似然,n是数据数量,k是模型的变量个数。python代码如下:
arma_mod20 = sm.tsa.ARIMA(data["xt"],(1,1,0)).fit()
arma_mod30 = sm.tsa.ARIMA(data["xt"],(0,1,1)).fit()
arma_mod40 = sm.tsa.ARIMA(data["xt"],(1,1,1)).fit()
values = [[arma_mod20.aic,arma_mod20.bic,arma_mod20.hqic],[arma_mod30.aic,arma_mod30.bic,arma_mod30.hqic],[arma_mod40.aic,arma_mod40.bic,arma_mod40.hqic]]
df = pd.DataFrame(values,index=["AR(1,1,0)","MA(0,1,1)","ARMA(1,1,1)"],columns=["AIC","BIC","hqic"])
df
AIC|BIC|hqic| AR(1,1,0)|253.09159|257.84215|254.74966 MA(0,1,1)|251.97340|256.72396|253.63147 ARMA(1,1,1)|254.09159|258.84535|259.74966
构造这些统计量所遵循的统计思想是一致的,就是在考虑拟合残差的同时,依自变量个数施加“惩罚”。但要注意的是,这些准则不能说明某一个模型的精确度,也即是说,对于三个模型A,B,C,我们能够判断出B模型是最好的,但不能保证B模型能够很好地刻画数据
参数估计
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(data["xt"], order=(0,1,1))
result = model.fit()
print(result.summary())
ARIMA Model Results
==============================================================================
Dep. Variable: D.xt No. Observations: 36
Model: ARIMA(0, 1, 1) Log Likelihood -122.987
Method: css-mle S.D. of innovations 7.309
Date: Tue, 22 Dec 2020 AIC 251.973
Time: 09:11:55 BIC 256.724
Sample: 01-01-1953 HQIC 253.631
- 01-01-1988
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 4.9956 2.014 2.481 0.013 1.048 8.943
ma.L1.D.xt 0.6710 0.165 4.071 0.000 0.348 0.994
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
MA.1 -1.4902 +0.0000j 1.4902 0.5000
-----------------------------------------------------------------------------
模型检验

参数的显著性检验


P<α,拒绝原假设,认为该参数显著非零MA(2)模型拟合该序列,残差序列已实现白噪声
模型的显著性检验

resid = result.resid#残差
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q', ax=ax, fit=True)
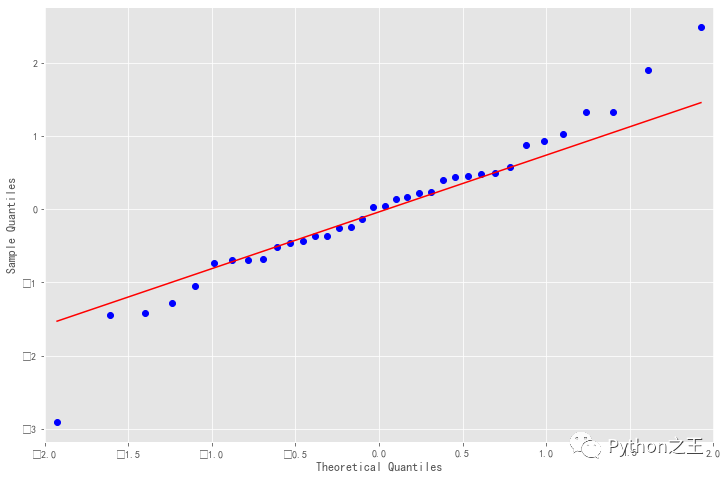
qq图显示,我们看到红色的KDE线与N(0,1)平行,这是残留物正太分布的良好指标,说明残差序列是白噪声序列,模型的信息的提取充分,当让大家也可以使用前面介绍的检验白噪声的方法LB统计量来检验
ARIMA(0,1,1)模型拟合该序列,残差序列已实现白噪声,且参数均显著非零。说明AR(0,11)模型是该序列的有效拟合模型
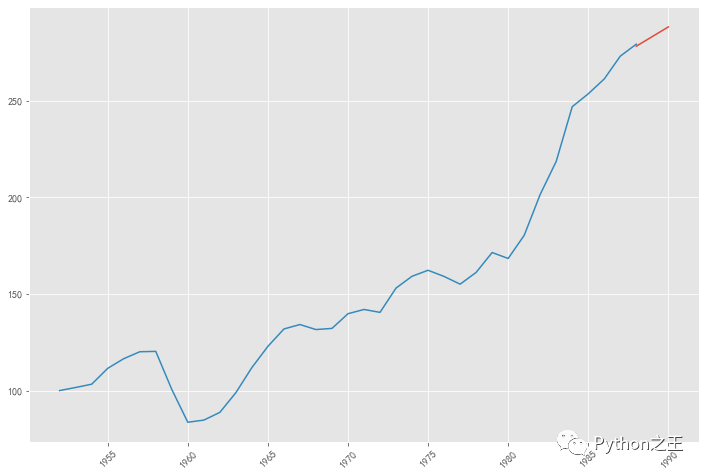
模型预测
pred = result.predict('1988', '1990',dynamic=True, typ='levels')
print (pred)
1988-01-01 278.35527
1989-01-01 283.35088
1990-01-01 288.34649
Freq: AS-JAN, dtype: float64
plt.figure(figsize=(12, 8))
plt.xticks(rotation=45)
plt.plot(pred)
plt.plot(data.xt)
plt.show()


Python“宝藏级”公众号【Python之王】专注于Python领域,会爬虫,数分,C++,tensorflow和Pytorch等等。
近 2年共原创 100+ 篇技术文章。创作的精品文章系列有:
日常收集整理了一批不错的 Python 学习资料,有需要的小伙可以自行免费领取。
获取方式如下:公众号回复资料。领取Python等系列笔记,项目,书籍,直接套上模板就可以用了。资料包含算法、python、算法小抄、力扣刷题手册和 C++ 等学习资料!
