「回归分析」知识点梳理
共 2379字，需浏览 5分钟
·
2020-11-24 15:29
↑↑↑点击上方蓝字，回复资料，10个G的惊喜
“正确问题的近似答案要比近似问题的精确答案更有价值”
这正是回归分析所追求的目标。它是最常用的预测建模技术之一，有助于在重要情况下做出更明智的决策。在本文中，我们将讨论什么是回归分析，它是如何工作的。
1
什么是回归分析？
回归分析是作为数据科学家需要掌握的第一个算法。它是数据分析中最常用的预测建模技术之一。即使在今天，大多数公司都使用回归技术来实现大规模决策。
要回答“什么是回归分析”这个问题，我们需要深入了解基本面。简单的回归分析定义是一种用于基于一个或多个独立变量（X）预测因变量（Y）的技术。
经典的回归方程看起来像这样：
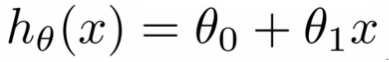
回归方程
回归分析源DataAspirant.com
在上面的等式中，hθ（x）是因变量Y，X是自变量，θ0是常数，并且θ1是回归系数。
2
回归分析的应用
回归分析用于在许多业务情况下做出决策。回归分析有三个主要应用：
解释他们理解困难的事情。例如，为什么客户服务电子邮件在上一季度有所下降。
预测重要的商业趋势。例如，明年会要求他们的产品看起来像什么？
选择不同的替代方案。例如，我们应该进行PPC（按点击付费）还是内容营销活动？
3
什么是不同类型的回归分析技术？
由于存在许多不同的回归分析技术，因此很难找到非常狭窄的回归分析定义。大多数人倾向于将两种常见的线性或逻辑回归中的任何一种应用于几乎每个回归问题。
但是，有许多可用的回归技术，不同的技术更适合于不同的问题。回归分析技术的类型基于：
自变量的数量（1,2或更多）
因变量的类型（分类，连续等）
回归线的形状
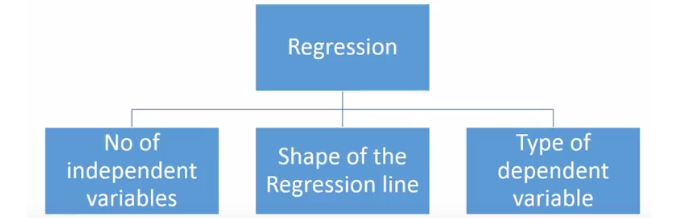回归分析技术
4
主要类型的回归分析
1. 线性回归
线性回归是最常用的回归技术。线性回归的目的是找到一个称为Y的连续响应变量的方程，它将是一个或多个变量（X）的函数。
因此，线性回归可以在仅知道X时预测Y的值。它不依赖于任何其他因素。
Y被称为标准变量，而X被称为预测变量。线性回归的目的是通过点找到称为回归线的最佳拟合线。这就是数学线性回归公式 /等式的样子：
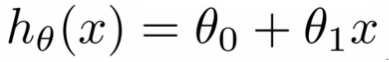
线性回归公式
在上面的等式中，hθ（x）是标准变量Y，X是预测变量，θ0是常数，并且θ1是回归系数
线性回归可以进一步分为多元回归分析和简单回归分析。在简单线性回归中，仅使用一个独立变量X来预测因变量Y的值。
另一方面，在多元回归分析中，使用多个自变量来预测Y，当然，在这两种情况下，只有一个变量Y，唯一的区别在于自变量的数量。
例如，如果我们仅根据平方英尺来预测公寓的租金，那么这是一个简单的线性回归。
另一方面，如果我们根据许多因素预测租金; 平方英尺，房产的位置和建筑物的年龄，然后它成为多元回归分析的一个例子。
2. Logistic回归
要理解什么是逻辑回归，我们必须首先理解它与线性回归的不同之处。为了理解线性回归和逻辑回归之间的差异，我们需要首先理解连续变量和分类变量之间的区别。
连续变量是数值。它们在任何两个给定值之间具有无限数量的值。示例包括视频的长度或收到付款的时间或城市的人口。
另一方面，分类变量具有不同的组或类别。它们可能有也可能没有逻辑顺序。示例包括性别，付款方式，年龄段等。
在线性回归中，因变量Y始终是连续变量。如果变量Y是分类变量，则不能应用线性回归。
如果Y是只有2个类的分类变量，则可以使用逻辑回归来克服此问题。这些问题也称为二元分类问题。
理解标准逻辑回归只能用于二元分类问题也很重要。如果Y具有多于2个类，则它变为多类分类，并且不能应用标准逻辑回归。
逻辑回归分析的最大优点之一是它可以计算事件的预测概率分数。这使其成为数据分析的宝贵预测建模技术。
3. 多项式回归
如果自变量（X）的幂大于1，那么它被称为多项式回归。这是多项式回归方程的样子：y = a + b * x ^ 3
与线性回归不同，最佳拟合线是直线，在多项式回归中，它是适合不同数据点的曲线。这是多项式回归方程的图形：
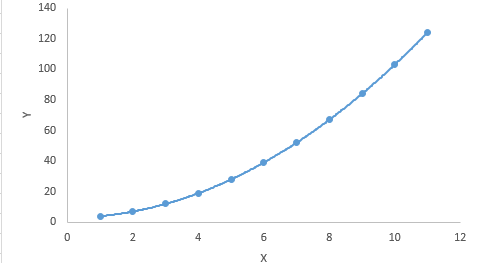
多项式回归
对于多项式方程，人们倾向于拟合更高次多项式，因为它导致更低的错误率。但是，这可能会导致过度拟合。确保曲线真正符合问题的本质非常重要。
检查曲线朝向两端并确保形状和趋势落实到位尤为重要。多项式越高，它在解释过程中产生奇怪结果的可能性就越大。
4. 逐步回归
当存在多个独立变量时，使用逐步回归。逐步回归的一个特点是自动选择自变量，而不涉及人的主观性。
像R-square和t-stats这样的统计值用于识别正确的自变量。当数据集具有高维度时，通常使用逐步回归。这是因为其目标是使用最少数量的变量最大化模型的预测能力。
逐步回归基于预定义的条件一次增加或减少一个共变量。它一直这样做，直到适合回归模型。
5. 岭回归
当自变量高度相关（多重共线性）时，使用岭回归。当自变量高度相关时，最小二乘估计的方差非常大。
结果，观察值与实际值有很大差异。岭回归通过在回归估计中增加一定程度的偏差来解决这个问题。这是岭回归方程式的样子：
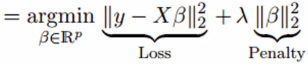
在上面的等式中，收缩参数λ（λ）用于解决多重共线性的问题。
6. 套索回归
就像岭回归一样，Lasso回归也使用收缩参数来解决多重共线性问题。它还通过提高准确性来帮助线性回归模型。
它与岭回归的不同之处在于惩罚函数使用绝对值而不是正方形。这是Lasso回归方程：
7. 弹性网络回归
ElasticNet回归方法线性地组合了Ridge和Lasso方法的L1和L2惩罚。以下是ElasticNet回归方程的样子：
