《规模》

各位好，今天我们讲的这本书叫作《规模》。这是一本让我耿耿于怀又大开眼界的书。为什么耿耿于怀呢？在几年前我读过这本书，但根本读不下去，读到一半我就放弃了，因为觉得有点难理解。最近我重新把它翻出来看，想趁着这个假期，使把劲，再试一次，我发现突然读懂了。这本书为什么又让我大开眼界呢？我们先看它研究什么问题。列举一些事实：所有哺乳动物的代谢率和体重之间的关系，我们很多人会自然地想到是不是成正比，其实没有那么简单，把它们的幂次放在坐标轴上，是一条斜线，这个斜线的关系就叫作非线性规模的缩放。

 

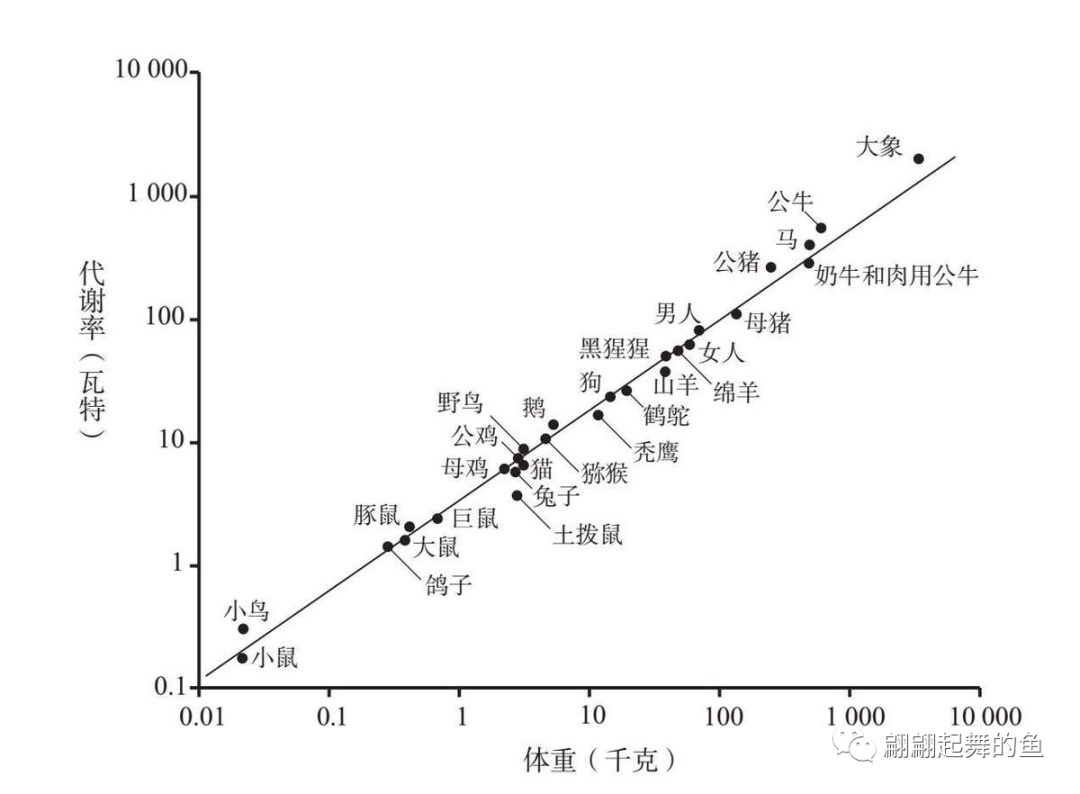
动物代谢率与其体重的关系

 

我这么说大家可能听不懂，比如说所有的哺乳动物，从像老鼠一样这么小的、最小号的哺乳动物鼩鼱，到最大号的哺乳动物蓝鲸（海里的那个100吨的蓝鲸），它们的寿命和体重有关系。这些哺乳动物的体重增加一倍，它的寿命相应大概增加25%，你就会发现所有的这些数字能够准确地排布在一条斜线上，虽然有偏差，但是不多，这是自然界当中非常神奇的一个现象。如果从自然界到人类社会，你会发现一个城市的专利数和人口之间也存在着这样的非线性规模缩放的关系，就是城市的规模每增加一倍（人口增加一倍），那么它的专利数也会相应地增加一个比例。一个公司的净收入和总资产，与它的雇员人数之间也不是简单的y=n*x的线性关系（人数只要翻一倍，它的净收入和总资产也会按照一个系数产生缩放），而是一个非线性规模缩放的关系。所以《规模》这本书讲的是什么呢，用一句话来概括，就是可量化的特点与规模存在着可量化的缩放关系。

 

这本书可以帮我们解决以下有趣的问题，比如说：

 

为什么我们最多只能活到120多岁，而不是1000岁或100万岁？（数学决定了人体有增长的极限，就是125岁就结束了。）
为什么身体成分与我们几乎相同的老鼠只能存活两三年时间，而大象却能活到75岁？尽管存在这样的差异，但是为何包括大象、老鼠在内的所有哺乳动物一生中的心跳次数几乎相同，都是大约15亿次？
为何几乎所有公司都只能生存数年时间，而城市却可以不断增长，而且能够避开即便是最强大、看上去最完美的公司也无法逃避的命运？（城市上千年的多的是，但是公司上百年的凤毛麟角。）
城市规模大小有限制吗？是否存在最优的规模？动物和植物的生长规模有限制吗？是否会出现巨型昆虫或者巨型城市？
为何生活节奏持续加速？为何创新速度必须持续加速才能维持社会经济生活？

 

这就是这本书要向我们解决的问题。本书的作者是圣塔菲研究所的所长，已经八十多岁了，他说这本书是写给“聪明的外行”看的。所以这本书里边没有数学公式，但你得懂什么叫作幂次。

 

那么接下来我们来了解规模法则的这个尺度是怎么建立的。首先说到一位几百年前的科学家——伽利略，这是大家的老朋友了。在伽利略的那个时代，昆虫科幻小说老喜欢写这种桥段：一个昆虫被辐射了，“砰”变得好大，苍蝇、跳蚤、蚊子都可以变得好大。但是伽利略当时就跟大家讲这不可能。为什么不可能呢？伽利略说如果它长这么大的话，它的腿立刻就断了，它根本哪儿都去不了。因为我们设计的这个动物是线性比例的增长，就是咱们从美术角度上看，线性比例把它放大，这不我还能认识吗，这就是蚊子。但是蚊子的腿只能承受小小的那个体重，蚊子的腿如果变得特别长的话，它承受不了自己变大后的体重。原因很简单，因为长度是一次幂，面积是两次幂，体积是三次幂。所以你的长度拉长了这么多，面积也要相应地增加（这是二次幂），体积的变化跟重量相关，变成了三次幂。所以它不是一个线性的、等比例的增长关系，而是一个超线性的关系。

 

所以我们得建立数量级的关系，理解数量级的关系最好的例子是地震。有时候我们听到消息，说哪个地方发生了里氏5.7级的地震，好像震感并不强烈，就是感觉到晃一晃，没出什么事。但是听说哪儿发生了6.7级的地震，那就可能会死很多人。为什么只差了1级，结果就差这么多呢？因为这里边的1级是一个叫数量级的差别，它是十倍地增长，这就是叫数量级的概念。

 

同样，我们要衡量哪个举重冠军劲儿更大，或者哪个举重冠军更强大，比如是重量级的举重冠军更强大，还是轻量级的举重冠军更强大？各位知道这个怎么衡量吗？画一条斜线，横轴是他们的体重，纵轴是他们所举起的力量。当然，要用对数绘制（像101倍、102倍、103倍、104倍……这样的比例被称作对数），把它变成数量级的关系。你会发现它是一条斜线，举重冠军的体重和他所举起来的重量是几乎在一条斜线之上分布的。那会有个别人跳脱开这条斜线，比如说那个最重量级的举重冠军，他在这条斜线的下方一点点，而那个中量级的冠军在这个斜线的上边一点点。谁是更强大的人？从绝对数字上看，重量级的选手肯定举的重量绝对数字更大，但是从强壮程度上看，谁超越自己的身体更多呢，是那个在这条斜线上方的中量级的冠军。这才是我们衡量一个人强大与否的非常重要的数据。这都是和我们直觉不一样的例子。人必须得理解数量级的概念，才能够更好地理解社会和自然界。

 

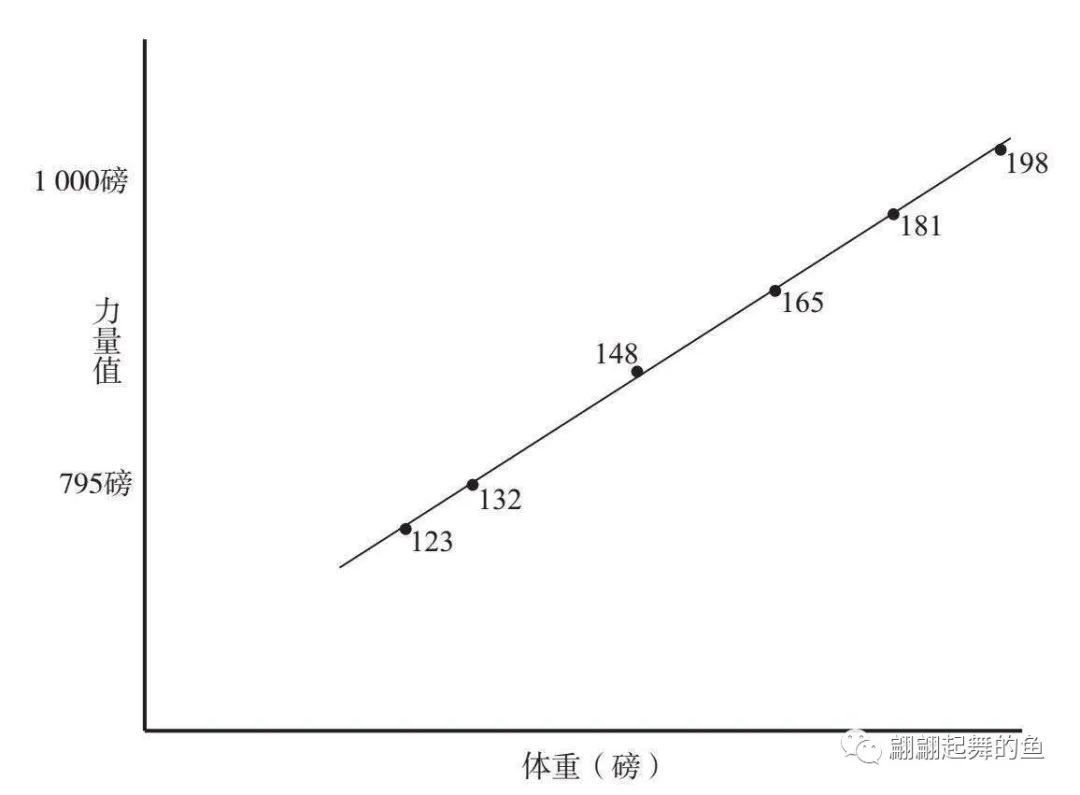
举重冠军的力量与其体重的关系图

 

曾经有人研究LSD（麦角乙二胺，是一种强烈的半人工致幻剂），研究LSD的药量到底应该怎么定。他们做实验，给老鼠吃致幻剂，发现效果很好，产生了相应的效果。然后他们决定放大一点药量，放在大象身上试试。他们怎么放大到大象身上的呢？这个不是虚构的，这是真实发生过的事，这些实验人员把老鼠的体重和大象的体重一称，算一下大概是多少倍，于是直接把老鼠的用药量乘了一下体重的倍数，把那么多剂量的致幻剂给大象吃，吃完之后大象立刻就死了。这个致幻剂本来的药效应该是迷幻，但是大象直接中毒死掉了。因为体重和药量之间绝对不是一个简单的线性关系，而是一个非线性的关系。

 

那么怎么才能够打破这个规模？如果我就要造一个像蚊子一样的大家伙怎么办？只能够靠创新。创新有两方面：一个是物质组成的创新；一个是结构设计的创新。就好像我们造大桥，最早人类造桥非常简单，就是在两岸架上木头，把板铺上，这个桥就造成了。但是当你要跨过一条长江造一个大桥，没有任何一个木头的结构能够承受。所以，过去人们认为这个桥根本造不了。直到有人开始发明斜拉索桥，斜拉索桥结构上完全变得不一样。但如果你说我就要一个细腿的大象，结构上不能够妥协，那你只能够在材料上下功夫，就是这个大象的腿肯定不是肉体，肯定是钢筋水泥。所以我们能够在游乐园看到大个儿的哥斯拉，材料跟我们人体都不一样，它是用钢筋水泥做成的，生物体要造成那个样子是几乎不可能的。

 

这里边插了一个科学史上的佳话，很有意思。2002年，BBC（英国广播公司）让英国人选出100位最伟大的英国人，排出来之后，大家能够想象到的，排第一名的是丘吉尔，第二名是谁呢？第二名这个人叫伊桑巴德。我们都不知道这个人，但他排在牛顿之前，排在霍金之前，排在莎士比亚之前，排在戴安娜王妃之前，排在贝克汉姆之前，这些英国人全都排在伊桑巴德后边。伊桑巴德是什么人？他是一位著名的工程师，这个工程师了不起的地方就在于他发现了规模效应。工业革命开始以后，人们学会了用内燃机造船，需要烧煤。那个船的体积都不大。后来有人说能不能造一些大轮船呢，很多船主说不可能。为什么不要造大轮船？因为大轮船烧燃料也多，把燃料堆满船舱就会把大出来的空间都占掉了，所以不要造那种大轮船，没有意义。但是伊桑巴德认为这个船的吃水面积增加和它的承载量的增加并不是一个简单的等比例关系，而是一个超线性缩放的关系，因为承载货物的增加更多的是来自体积的这种变化。经过计算，他认为如果一个船造得更大，所增加的燃料并不是它体积的一倍，而是比体积要小得多，所以才开始造大型的蒸汽船。这就是规模在经济上的运用。还包括斜拉索桥，最早的斜拉索桥就是由伊桑巴德造出来的，他是一个懂得规模效应的人。

 

接下来我们来回答前面那些奇奇怪怪的问题。首先进入生命的状态。生命跨越了30多个数量级，什么叫30多个数量级呢？生命的跨度是从100（是1）能够到1030那么大。生命的跨度是极其大的，但是这个非常大的跨度依然有着很明显的缩放的关系。“从复杂分子、微生物到鲸、红杉，生命非凡的跨度堪比从银河系到亚原子的跨度。”从一个亚原子到银河系这么大的缩放程度，就是生命的巨大的跨度。

 

研究生命就要研究代谢率，什么是代谢率呢？就是我们的生命之火。各位知道，我们人的代谢率是多少吗？一个人如果在野地里边生活，消耗的能量相当于一个90瓦特白炽灯泡的代谢率。但是你知道咱们生活在上海或者生活在北京，我们一个人的代谢率有多少吗？差不多能够达到1.1万瓦特。因为我们需要穿衣服、需要出门、需要坐公交车、需要吹空调，我们的代谢率就一下子猛增。除人类之外，动物随着体积的增加，代谢率会下降，就是会变得更加节能。然后再经过自然选择，慢慢地形成了一条叫非线性缩放的斜线。如果一只猫的体重比小老鼠大100倍（这是有可能的，小老鼠和一只比较大的猫体重差100倍），那么猫的能量消耗是这个老鼠的32倍，而不是100倍。因为体重每翻一倍，这只猫的代谢量就要节约25%，每翻一倍就要节约25%，这是一个幂次的关系。所以翻了100倍以后，猫的代谢率只是老鼠的32倍，而不是100倍。这个不只是猫和老鼠，所有的哺乳动物都一样，每翻一番节约25%的能量，相应地，细胞损伤率也会下降25%，所以动物的寿命也会变得不一样。

 

“除了代谢率，它还包括诸如增长率、基因组长度、主动脉长度、树木高度、大脑灰质数量、进化速度和寿命等，可能有超过50种这样的规模法则，令人吃惊的是，它们的对应指数都接近1/4的整数倍。”这是一个非常神奇的数字——4。就是这50多种不同数据的缩放的斜线的斜率，要么是1/4的比例，要么是2/4，要么是3/4，都是1/4的整数倍。

 

那么这个“4”是从哪儿来的呢？为什么生物界当中会出现这么一个神奇的数字“4”？接下来，我们就来揭秘这个事。首先生物是靠能量的传递活下去的，也就是说我们这个身体形态最终的目的是要把能量传递到每一个终端。我们的手指不能是麻木的，它肯定得有能量过来。然后随着这个涌现的规律，以及我们自身就是一个巨大的网络体系，我们得不断地优化。这个优化的结果就形成了今天的这个数字“4”。这里有三个最基本的限制条件。第一个，空间填充。我们体内是由管道构成的，比如血管、神经、淋巴全都是管道，所以基本上我们的人体是管道组成的一个结构。这是空间填充的说明。第二个，终端单元的恒定性，这一点是让我觉得最神奇的。什么叫终端单元的恒定性？你去看树叶，植物有大有小，红杉特别粗，小月季花是细细的，但它们树叶的叶柄粗细是一样的。你没见过（像手腕）这么粗的叶柄吧，有哪个树叶的叶柄这么粗。我们说这树大，所以这叶柄这么粗，没有这样的树。大白杨树的叶柄也是细细的，差别不大。这就叫作终端的恒定性。人的毛细血管的粗细和鼩鼱是一样的，和大象是一样的，和海里的蓝鲸是一样的。也就是说，蓝鲸的身体重量一百吨，但它的毛细血管到了最终的终端时候跟人类一样，跟小老鼠一样，都是那么细。但是我们的出发点不一样，动脉的粗细程度是不一样的。而从主动脉到毛细血管，所有的哺乳动物几乎都是15个层级，15个层级缩放到毛细血管这个状态。这是第二个限制条件，就是终端是一样的。第三个，优化。优化的目的就是能量的最小化，不要让身体消耗过多的能量。大自然就是这样，一点都不浪费，它是用能耗最小的方式排布一切。

 

把这三个条件放在这儿，大自然就开始往你体内塞东西了，就是你要怎么长才能够符合这三个条件。我们要知道血液流动的过程，血液首先从我们的主动脉出发，心脏左心室一挤压，血液就出来了。那个血液是波动的，就像交流电一样，血液不是平缓地流过来的，血液要有足够的力量，如果没有足够的力量，是冲不到终端的。所以那么大的血压一挤，“砰”，血液是波动过来的。从粗的血管里边波动过来的力量到了前面，血管要分支让血液流走。你注意如果有阻碍，这个波浪形的血液就会倒流，就像一个海浪打到墙上那样倒流回去。

 

那波动的波浪到前面分叉的血管的时候，怎么能够直接就冲进去，而不会再倒流回来呢？这里边有一个非常重要的数学原理，就是等面积原理。也就是说，假如我这一个管子要分成两个管子，那么这两个管子的面积加在一起，要跟总的管子一样大，所以它们的半径之间的关系就能够算得出来了，一定跟根号2是有关系的。因为圆的面积公式是πr²，你把总管子（这是一个πr²）变成两个管子（两个πr²），那么它的半径一定是跟根号2有关，是以根号2为单位的一个缩放的关系。最神奇的是，达·芬奇知道这一切。这个作者说，达·芬奇在文艺复兴时期（我们讲过《列奥纳多·达·芬奇传》这本书）自己去画那个血管的关系，并且注释说这个血管的分叉面积是一样的。这简直不得了，太神了。

 

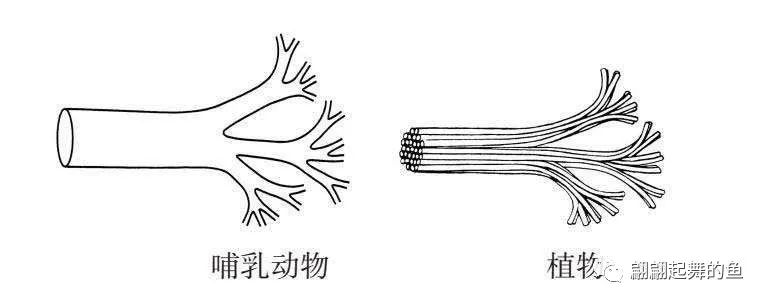
等面积分支结构图

 

因为有着这么一个根号2的关系，血管不断地用这样同样的比例分叉，这是不是就是一个非线性的关系，在不断地用根号2这个数字不断地分，始终保持每一次分下去，血管的总面积是一样的，这样就形成了最后的这个数学的关系。也就是为什么是1/4、3/4，作者忽略了这个推演的过程，总之是经过非常复杂的计算，那如果你有数学根基，可以自己算一下。

 

最后血液是怎么停的呢？血液流过去以后，一直都这么波动、波动、波动，直到什么时候它可以供氧了呢？就是等它流到那个细细的毛细血管里边以后，因为血液有黏滞力，不再波动了，变成了静静地流动。最后到终端，静脉上的血液流速大概只有每秒1毫米，血液到了毛细血管处只有每秒1毫米的速度。所以你拿个针扎一下，发现那个血液是慢慢涌出来的，但你要试着在动脉上来一下，那个速度是每秒40厘米，就直接喷溅出来了。

 

血管、树叶、西蓝花、海岸线这些东西都是一个典型的分形组织。你拿一个西蓝花，一个大的西蓝花你会觉得这是个西蓝花，你掰一小块下来看，还是个西蓝花，再掰一小块看，还是个西蓝花。你哪怕掰到最后剩一个渣儿，拿放大镜看，还是一个西蓝花，这就是典型的分形。大自然当中充满了分形。这种分形体系当中的数学，是由一个叫作曼德尔布罗的人研究出来的，有一个数字叫分形维数。为什么我们体内是跟4这么一个数字有关呢？就是除了我们的三维（长、宽、高）之外，还有一个分形维数。假如这个动物的腿就是一个平滑的立方体，没有任何分形维数，那么就是“3”这个数字，幂次关系就是1/3，而不是1/4。但是因为我们所有的形体都不是平滑的，而是充满了分形的，我们体内的肠道、血管都是充满了分形的，所以多了一个分形维数，就变成了4。现在弦理论科学家研究5维、6维、11维空间，他们说最多有11维空间。如果在11维空间当中这个分形再加一个分形维数1，就应该是1/12的关系。这个我知道挺难理解的，你们去看《星际穿越》这部电影，大概能够找到这种感觉。

 

我们在讲《深奥的简洁》那本书的时候，有一章讲的是1/f频率。我相信很多人不理解什么叫1/f频率，也就是说对于光滑的非分形体系来讲，可能就是1/3频率；对于人这样的三维动物来讲，我们就是三维再加1，就是1/4频率；如果是一个11维的生物，虽然咱们不知道是什么，那么它的数字是符合1/12频率的，这个就叫作1/f频率。这个1/f频率存在于生活中的方方面面，你把乐队演奏的乐曲拿出来，把各种音出现的频次求对数，你会发现它们的关系是完整的一条斜线。音乐如果是噪声，没法成为一条斜线，但是好听的音乐就是在一条斜线上，这个就是1/f频率所起的作用。生命产生了这样的节律，我们能够如此完美地生活在这个世界上，我们一定要符合一些规律，而这个规律就是1/4的规律。

 

对于分形最有意思的研究，是曼德尔布罗（世界“分形几何之父”）他们当年发现，想要测量挪威的海岸线到底有多长，这是不可能的一件事。为什么呢？因为它完全取决于尺度，而海岸线是参差不齐的，所以假如你用直线“哐哐哐”画这么几下，会得到一个数字，假如你说10公里之内一定要绕弯儿，以10公里为单位绕弯儿，又得到一个新的数字。然后假如你说不行，1公里的弯儿都要绕，那是更大的数字，永远测不完，你永远不知道挪威的海岸线到底有多长。这就是一个典形的分形体系。最后只好加入一个分形维度，找到一个大概的、趋近的极限值，你大概可以这样理解。所以，因为我们有了分形维度之后，把一个三维再加一个1，变成了以4为单位的比例。

 

那为什么没有更小的哺乳动物呢？现在看到最小的哺乳动物是鼩鼱，大概几厘米长。为什么不能有一个像跳蚤一样，或者像蚊子一样的哺乳动物，原因是什么？因为脉动的血液至少要通过第一个分支，就是鼩鼱的主动脉已经短到只有几毫米了，已经相当短了，但是它至少还要脉动一下才能够进入到静脉当中，这是哺乳动物的一个特点。那如果体积再小，你就会发现它连最初的那一个小小的脉动都达不到了，就不能够产生哺乳动物的特点。

 

那为什么不能有更大的哺乳动物呢？同样的道理，我给大家念一下，如果真的有哥斯拉的话会是什么样子：“在其最新形象中，哥斯拉长达350英尺，转化为重量约为2万吨，是最大的蓝鲸的100倍。为了维持身体的巨大组织，哥斯拉必须每天进食25吨，相当于每天代谢约2000万卡路里的能量，这些食物足够维持一个1万人的小镇。它的心脏重约100吨，直径约为50英尺，需要为身体其他组织泵出200万升血液。然而，为了平衡这一点，它的心脏每分钟只需搏动几次，就能维持与人类相似的血压（一分钟三四次就够了）。……哥斯拉的寿命可能达到2000年，每天睡不到1个小时。……每天产生尿液2万升，相当于一个小型游泳池的水量；产生粪便3吨。”作者说，如果你问一个物理学家哥斯拉会不会存在，他只要简单地告诉你不会。但是如果你问他假如哥斯拉存在的话是什么样子，那就是这个样子。整个自然界没有进化出比蓝鲸更大的海洋生物，也没有进化出比恐龙更大的陆生动物，可能就是因为规模受限，我们的规模就到这儿，没法把它变得更大了。

 

最后说到生命的死亡问题，其实医学对于人平均寿命的增长最大的贡献是婴儿死亡率的降低。我们过去说平均寿命是30岁或者40岁，是因为婴儿寿命特别低。各种疾病的减少，实际上并没有让寿命像我们想象的那样大幅度增长。“如果你在1845年活到了25岁（1845年的平均寿命是30多岁，很低），那么你的预期寿命就会从40岁延长到62岁。另一方面，如果你活到了80岁，那么你很可能活到85岁。但是这和如今的情况相差无几；如果你今年80岁，你很可能只能活到89岁。”也就是说在长寿这件事情上，我们后端所做的变化并不多，更多的是婴儿死亡率的变化。“假如你在1845年活到100岁，那么从数据上说你可能只能再活两年不到——精确地讲，只有一年零十个月。如果你今天活到了100岁，你可能还能再多活两年多一点。”你发现越往后这个差距越小，就是你的寿命比150年前的前辈活到了100岁以后，其实只增长了5个月。那为什么会这样呢？人类这么厉害，医学上做了这么多的进步，但是我们始终就维持在100岁左右，那么人类的寿命到底有没有一个极限呢？很不幸地告诉大家，根据这个规模的算法，就是125岁。到125岁左右的时候，你的细胞基本上就全部磨损完了。那你说我可以把我的大脑提取出来变成数字化的信息，那是另外一件事，你肉体不会再有了。至于你那个数字化的信息还能不能够有你的想法，那跟这个不是一回事，你的肉体已经消亡。

现在世界上已知的最年长的人叫让娜（让娜·卡尔曼特），是一个法国老太太。这个老太太见过梵高，她到现在都还记得梵高到她叔叔的店里来买东西的场景。老太太活了120多岁，太厉害了。（科学家对存活曲线和死亡曲线进行统计分析，得出了令人惊讶的结论。）这个非常令人惊讶的结论是什么呢？“大多数生物体的死亡率与年龄是不相关的！换句话说，无论年龄几何，在任意一个时间段内死亡的相对个体数量都是相同的。如果5%的人口在5~6岁之间死亡，那么45~46岁之间，或95~96岁之间的死亡率，同样也是5%。……一个恒定的死亡率意味着在某个时间段内死亡的个体数与存活到该时间点的个体数成正比。……个体存活率遵循一个简单的指数曲线，这意味着随着年龄的增长、个体存活的概率呈指数级减少。换句话说，个体死亡的概率呈指数级增加。”

 

虽然你在这一个时间段内的死亡率是一样的，但是进入到这个时间段内的人数本来就是指数级地下降，所以每一个层级占比是5%，每一个层级占比是5%。你想想看最后累积到最老的那个层级，实际上留下来的人就已经很少了，这依然是一个指数级的分布，而不是一个等比例的分布。总之，人类的寿命的边界就是125年左右。“如果可以治愈所有的心脏病和心血管疾病（你们觉得这样是不是很了不起，人类再也没有心血管疾病和心脏病），那么人们出生时的预期寿命仅会延长6年。更令人惊讶的一点是，如果可以治愈所有的癌症，那么人们出生时的预期寿命只会延长三年左右；而相对于65岁的人群来讲，预期寿命只会延长不到两年。”这是关于规模在生命里边的好玩的原理。

 

接下来我们看城市。首先，城市到底是不是一个生命？这个作者说城市是人类造出的最大的生命体。城市是指数级增长的，城市的人口是指数级增长的，城市的GDP也是指数级增长的，这两个东西（城市人口和GDP）之间是存在着非线性的相关关系的。在一个封闭系统内的增长曲线，这个大家应该都很熟悉，无论你去研究企业的生命周期，还是研究一个人的成长、死亡，都是这么一条曲线。一开始第一个阶段叫迟缓，像现在创业，刚开始不知道该干什么，干了3个月没什么动静，这是迟缓。迟缓期过了以后，突然找着门道了，开始上升，这个叫指数级的爆发。就像帆书（原樊登读书）在三五年前出现指数级的爆发。然后是稳定，就是一直都是这么一个样子，就像我们现在的身体状况，就是稳定。等过了50岁，开始衰老，就是衰亡期。所有的生命体的生长过程都是这样一条曲线。我们过去经常讲，一个企业的S曲线就是到平缓的稳定期这里，没有说往下衰亡的事。实际上，城市也是符合这样一条曲线。

 

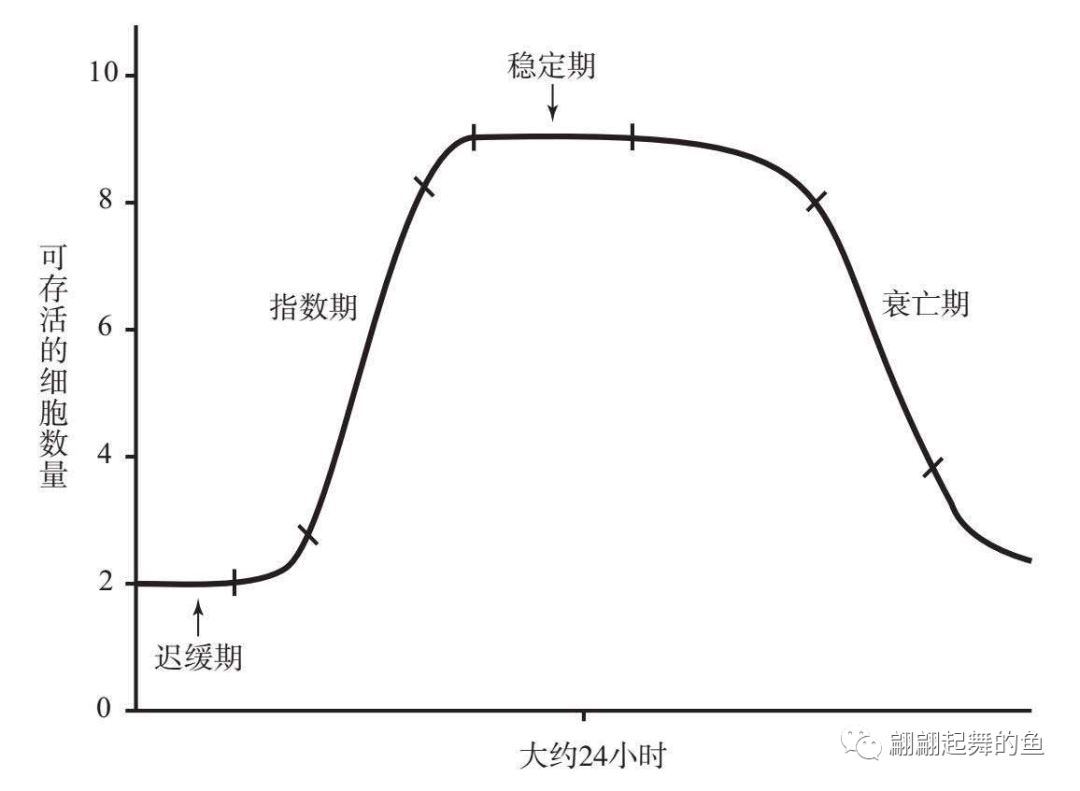
封闭系统的增长曲线

 

人类有两次巨大的革命：一次是农业革命，一次是工业革命。农业革命使得我们能够种植，能够驯化了小麦。工业革命让我们使用了这些生物能源，我们可以开始造机器。这两次革命都使得人类产生了一个指数级的变化。在未来30年之内，在这个世界上每周会产生一个150万人的城市。全世界都在不断地造城市，我们说中国的城镇化还刚刚开始，非洲还有很多地方需要城镇化，所以很多地方都在造着大量的城市。这里边出现了马尔萨斯式的恐怖预言，马尔萨斯（英国经济学家）说人口的增长是几何级数的，而我们的自然资源是有限的，所以总有一天得死很多人，否则这个地球就没法平衡，所以人们开始计划生育。但是很多人反对马尔萨斯，说这个说法根本就不对。为什么呢？这种人叫作创新乐观主义者，创新乐观主义者认为你要相信创新，如果你用17世纪的方式养活地球上这么多的人，那肯定不行，都饿死了。但是因为有了牛顿，进而产生了工业革命，进而产生了新的能源，人们发现了石油，我们现在能养活这么多的人，未来我们还有太阳能，可能还会有氢能、核能，我们能够养活更多的人。所以这是两种完全不同的观点。你们知道，太阳每年往地球上发散的热量有多少吗？有1018千瓦，这个幂次太大了，所以一般理解不了，换算成能听懂的话，就是每小时太阳发射到地球上的能量够地球人用一年。所以，乐观的说法是你不用太过担心能量的问题，因为只要你太阳能做得好，一小时够你用一年了。

 

在古罗马的时候，有一个执政官跟他的市民对话，他说“城市即人”，没想到这句话是一句科学的话。为什么说“城市即人”呢？我们刚才讲那个1/4比例的时候，说到了三个非常重要的约束条件，还记得吗？第一个是空间填充，第二个是节能（优化），第三个是终端恒定性。这三个条件城市都符合。城市就是一个空间填充的过程，比如建楼、建路，把这个城市填充起来。然后城市要节能，就是我们不能够乱花钱，我们不能够造“鬼城”。你会发现凡是主观意识特别强的时候，想着“我要建一个鬼城，我自己建，不管有没有人住”，这就变成了一个伤疤。但是如果是老百姓慢慢地衍生，慢慢地生活，慢慢地购买，你会发现那个城市是有机生长出来的。第三个就是终端恒定性，这个楼比你们家大概大100倍，这个楼的插座会比你们家的插座大100倍吗？你想象这个楼的电源插座（像电视机）这么大，不可能。再大的大楼，电源插座都是一样的。再大的大楼，水管子的粗细都是一样的，网线粗细都是一样的。这跟毛细血管的道理是一模一样的。所以城市都符合生物体的这些限制条件，因此城市也是按比例缩放的。但是这个比例的数值跟生物体是不一样的，这个比例是85%，每增加一倍的体量，我们的能耗能够减少15%，跟生物体有着这样一个区别。这里边包括城市的工资总额、专利数量、犯罪率、餐厅以及GDP，都是跟85%有关的。

 

给大家看一下这张图，你就明白了。这张图是法国、德国、荷兰、西班牙四个国家，横轴是它们城市规模的幂次，比如102、103等；竖轴是加油站的数量，也是按幂次分布的。你会发现，几乎都在一条斜线上。我们把这些数据进行了幂次的处理以后，发现它们几乎都在一条斜线上，偶尔有上下浮动，可能多一点或少一点，但是几乎都在这条斜线的附近徘徊。这就是85%的这个比率，人口规模每增加一倍，城市只需要增加85%的加油站，也就是说每增加一倍，我们就节余了15%的能量，这个和生物体是有非常相近之处的。

 

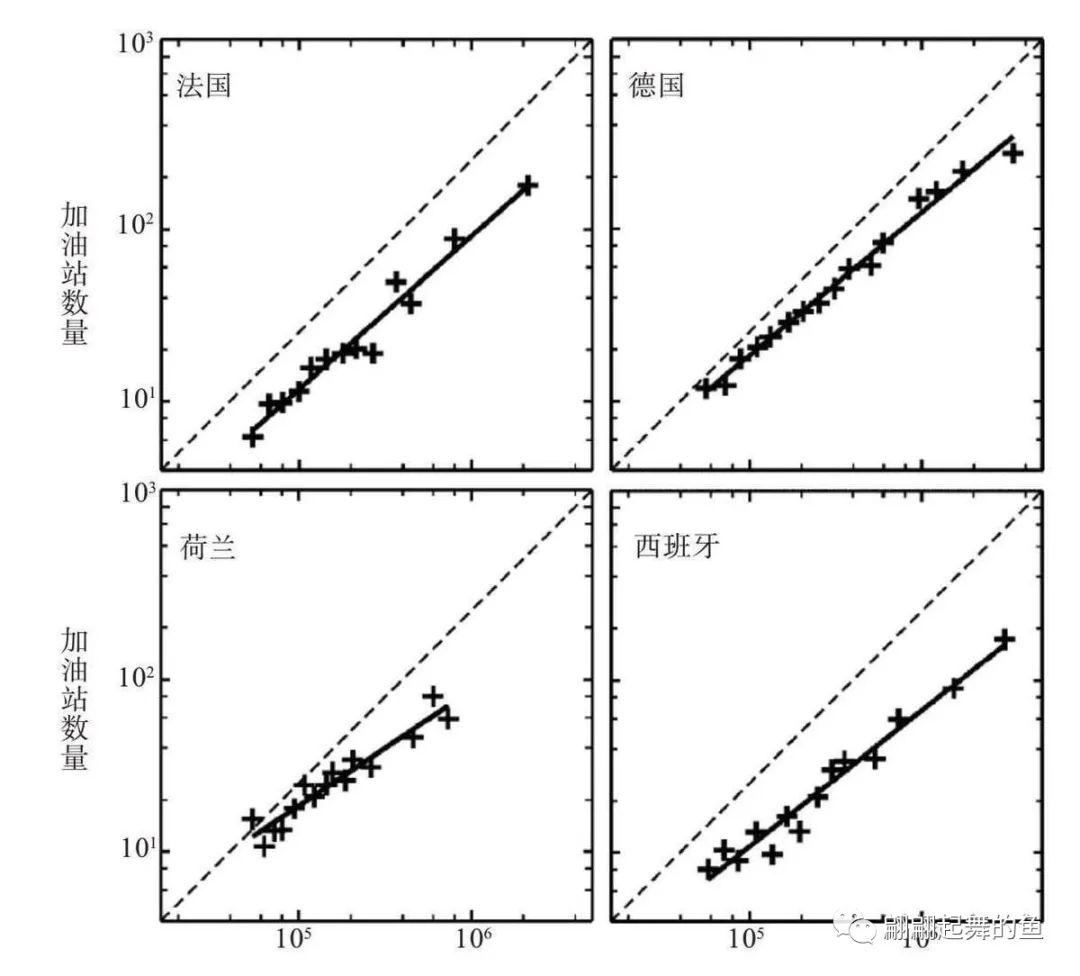
加油站数量与城市规模的关系图

 

“我们总结一下：城市越大，社会活动越丰富，机会越多，工资越高，多样性越丰富，享受好餐馆、音乐会、博物馆和教育设施的机会也更多，繁荣、兴奋和参与感也明显增加。与此同时，人们也无法超越、忽视或者低估不可避免的负面因素以及不断增多的犯罪、污染、疾病等阴暗面。人类很擅长‘趋利避害’。”就是你的规模增加一倍，你的犯罪率也会增加85%。不过好消息是规模增加一倍，犯罪率并没有翻番，犯罪率只是增加了85%。“个人利益和集体利益随着城市规模的增大而系统性增加，这已经成为全球城市化持续爆炸式增长的潜在驱动力。”这话什么意思呢？就是所有生活在这个城市里的人都是理性的人，都会做出选择，所以你必须得节省能量。假如你说咱们生活在城市里的人不节省能量，我们就按照方块化来生活，谁让我去哪个方块，我就去哪个方块。多花多少钱我都不管，多消耗多少能量我都不管，那么这个城市就不是一个生命体。而这个城市就是由我们这些普通的、想要省钱的人构成的，所以我们会节省能量、节省钱。

 

最有意思的事是世界上有很多方块的城市，比如说西安。你打开看西安地图，发现全是方块，方方正正的。如果我们按照唐朝的规划，或者明朝的规划，我们把这个方块的城市放在地图上，你看不出它有生物态的感觉。但如果天黑以后，你到天空中拍一个航拍图，你就会发现西安市里边的灯火明灭不是按照那个方块来的，而是像一个细菌的形状一样延伸出去的，就跟那个细菌放大的照片几乎是一模一样的。还有一个国家也是方块，美国。美国的所有的州都是方块的（它们是一个一个买回来的），这个方块的州表面看起来是人为设计的一个版图，夜间从太空当中拍一张照片，跟细菌的形状一样，延伸出来那种分形的体系。城市也是按照规模的比例在缩放的，因为城市当中存在很多的网，比如说水管、电线、马路，还有信息流等，所以城市不是一个晶体状的，而是一个分形体系。

 

有一个很有意思的研究，就是城市里人们走路的速度也是按照规模缩放的。城市的人口只要增加一倍，每个人走路的速度就会增加百分之多少（这个数字当然会小一点，不会特快，因为人是受生理影响的）。你到香港的街头去，就是会走得快一点；你到上海的街头走，你就会走得快一点；你到阆中古镇或者到香格里拉去，就会走得慢一点。所以，人口的增加会带来这种变化。还有一个数字，就是人的交往。有的人很善于社交，有的人不善于社交，但是几乎所有人社交的人数都是差不多的。这个研究是关于邓巴数，邓巴数很有意思，它其实也是一个幂次的分布关系。给你们看一下这张图：

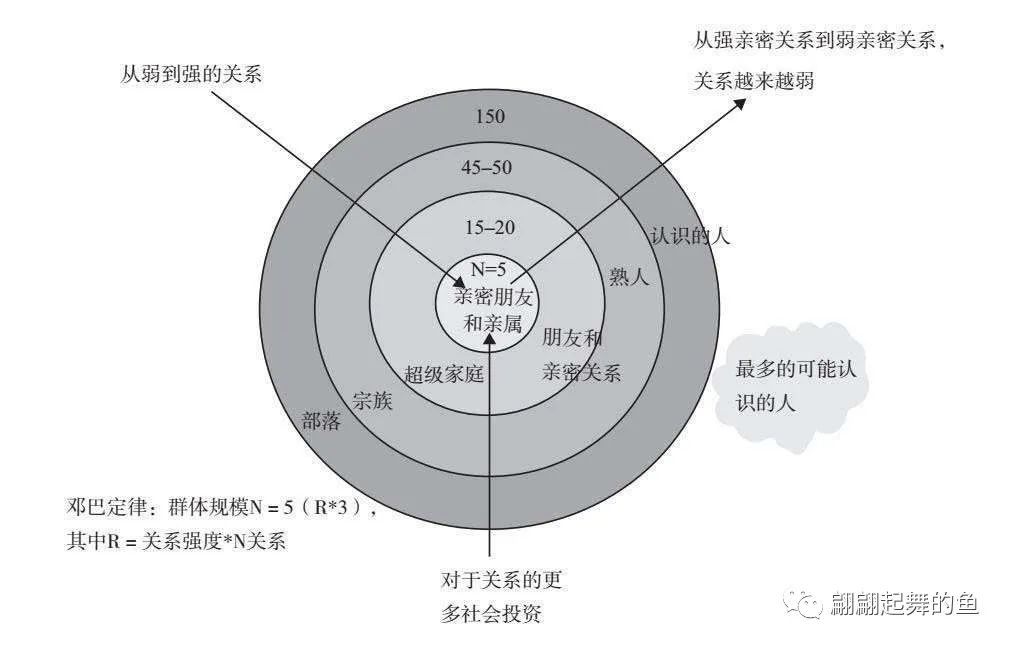
邓巴数是什么呢？我们每一个人大概有这么几种朋友，最核心的朋友叫作亲密朋友和亲属，这个人数一般来讲5个人。然后外边这一圈是朋友，包括超级家庭、亲密关系，就是你非常亲近的这些朋友，这个人数大概是15~20个。再往外一圈是熟人，也就是我们古代讲的家族，这个人数大概是45~50人。最外边一圈，古代的时候叫作部落，就是我们认识的人，大概150个左右。这就是我们所说的邓巴数。人的交往其实也是受到限制，你不可能说我想认识很多的人。我手机里边大概有6000多人，但是很多人根本叫不上名字，或者根本没有见过，你能够记得名字的可能就是100多个人。这是关于城市的一些研究。

 

最后总结城市的特点，首先，越大的城市生活节奏越快，我们刚才讲了。无论在哪里，人们的通勤时间大致相同。比如说你在上海，你住在郊外，上班可能需要半个小时到一个小时。我今天早上住在公司隔壁的酒店，不太远，隔着一个街区，早上起来大家说叫车吧，我说别叫车了，这么近，走过去，到公司也是半个小时。有的人说我就住家属院，旁边就是办公楼，我要去上班，五分钟就走到了。那么你这一天会拿更多的时间散步，把走路的时间补出来。很奇怪，人每天就是想在户外走一个小时。所以，通勤的时间几乎是相同的。这个规律叫作马尔凯蒂规律。然后，大城市通话时长更长，就是每天会有更多的人跟你聊天，会有更多的人跟你通话。

 

还有一个对于城市规划非常重要的概念，叫作“旅行地的平方反比定律”，人们到一个地方的频率跟距离的平方反比是相关的。我得念一下这个具体的数字，因为很容易说错。“假设平均有1600人每月有一次从4公里远的地方到波士顿公园街周边地区。那么，会有多少人从两倍远的距离（也就是8公里），以相同的频次，即每月一次到访公园街呢？平方反比定律告诉我们，会有1/4（因为翻了一倍，1/22）的人到访该地。因此，只有400人从8公里远的地方每月一次到公园街。那么，假如那个人住的距离是5倍远呢？答案是1/25（1/52）的人，也就是只有64个人。”因此，区位还是很重要的。我们很难通过自己的主观想象，说我要在这里举办一个活动，这样的话人就都来了，未必如此。你要算清楚你的周边到底有多少人，跟距离的平方反比是有关系的。当然有例外，但是这些例外都是那些热点，比如说去澳门你一定会去大三巴牌坊，你没去大三巴牌坊相当于没有去澳门，所以澳门大三巴牌坊可能会突破这个比率。还包括陕西的兵马俑，可能会突破这个比率。但是一个普通的景点是很难突破这个比率的。这是关于旅行地的平方反比。

 

还包括城市排名，我们现在经常排名城市，都是按GDP排名。按GDP排名的话，北上广肯定排在前边。但是北上广真的就是最健康的城市吗，或者经济最有活力的城市吗？体量大未必最有活力。还记得我们说那个举重冠军的事吗，你应该画一条幂次的非线性相关的斜线，然后看哪些城市最有活力。横轴是城市规模，纵轴是城市的GDP，都是幂次数据，那么它会是一条直直的斜线。如果这个城市在斜线的上方，这才是更有活力的城市。即使它体量小，但它的经济活力比较好。在斜线下方，就算体量大，它的活力在下降。这才是进行城市排名的有效方法。

 

还有行业多样性的问题。一个城市里边的企业数和人口呈线性关系，不是非线性关系。这个线性关系就容易理解，每增加22个人就会多一个就业场所，这是一个基本的y=n*x的线性关系。但是行业多样性却不一样，也就是说虽然多了这么多的企业，但是创新型企业的出现是非常有限的，“人口规模从10万增至1000万，会导致企业数量增加100倍，但企业的多样性只会增长两倍。换句话说，城市规模增长一倍，企业总量增长一倍，但新型企业的数量只会增长5%。”所以，创新是一件非常不容易的事。以上就是我们讲的关于城市这个生命体的特点。


最后一部分关于企业。企业主要是由三个东西决定的：交易成本、组织结构和市场竞争。这跟我们前面讲的三个约束条件是非常像的，就是你把企业的规模和它的寿命、规模和它的收入、规模和平均工资等等画在一起，是什么样子呢？很有意思，就是虽然方差较大，但它们依然是在一条斜线上徘徊。

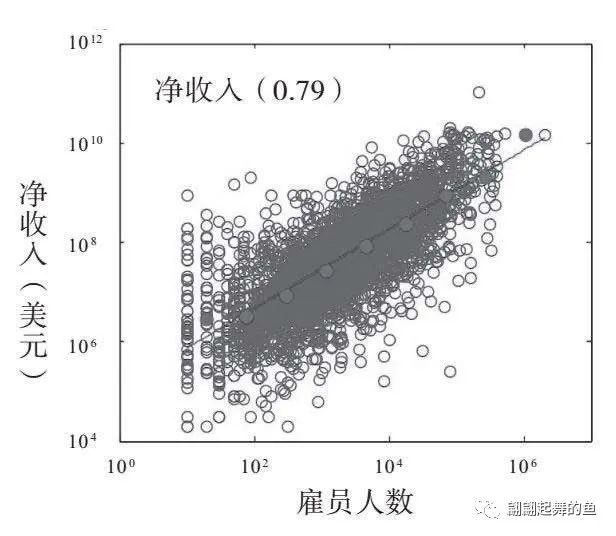
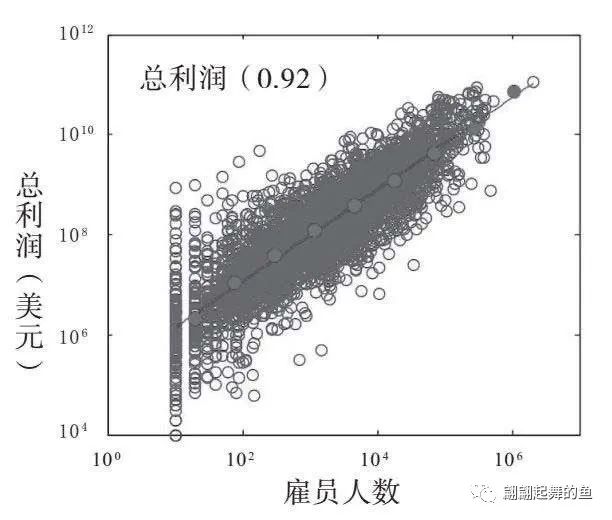
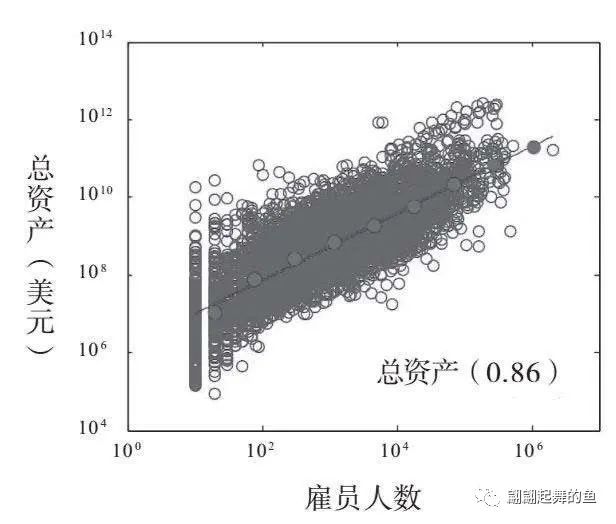
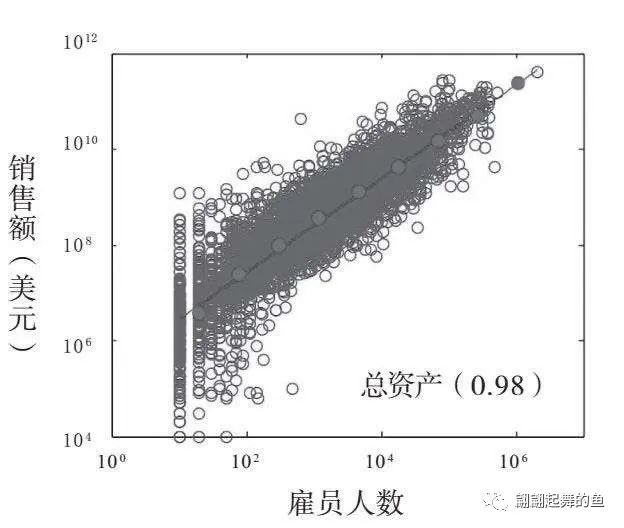
1950—2009年间美国28853家上市公司的净收入、总利润、总资产和销售额与雇员人数的关系

 

这里的斜线很粗，不像城市的关系图那么漂亮，城市是非常漂亮地排在这个斜线上。举重冠军的分析图，大象、蓝鲸的分析图，都是非常漂亮的一条斜线。但是公司这里变粗了，粗意味着方差大，就是例外的幅度会多一点，但是也基本上形成了一个幂次相关的非线性的相关关系。这个图是1950年到2009年美国28853家上市公司的净收入、总利润、总资产和销售额与它们的雇员人数的对数坐标绘图，显示出较大方差的亚线性比例变化。所以，公司竟然也是一个生物体，也能够有相应的规模缩放。

 

那么我们最关注的问题是为什么公司短命。公司的半衰期大概是10.5年，10.5年意味着什么呢？就是过10.5年有一半的公司就消失了。“从1950年以来美国公开上市的28853家企业中，截至2009年，共有22469家公司已经消亡。其中有45%是被其他公司并购，只有9%破产清算，3%被私有化，0.5%经历了杠杆收购，0.5%被反收购，剩余的则是其他原因导致的消亡。”作者花了5万美元才拿到了标准普尔的这个数据，他耿耿于怀，说竟然要花钱。“幸存公司的数量在公开上市之后便迅速减少，不足5%的公司存活时间超过30年。相类似的是，死亡曲线显示，在50年内，死亡公司几乎占到了100%，其中50%在不到10年的时间里便告‘死亡’。作为一家公司，要想存活下来真的太难了！”

 

但是你们也不要因此而害怕，为什么呢？什么叫“没有了”，被并购也是没有的一种方式，就是你做到一定的程度以后，你的竞争对手比你更厉害，你也在增长，只是你的增长速度低于市场的增长速度，你能活下去，但你可能会被别人收购。为什么企业的寿命这么短，很大的原因是因为城市没法并购，企业虽然现金流是正向的，但是增长速度赶不上市场增长速度的时候，也就是说市场的大浪淹过了你的鼻子，这时候你就可以宣告“死亡”了，因为你被别人买走了，这其实也是一种很不错的退出机制。一个人做公司做到能够被人买掉，这是非常好的退出机制。

 

除此之外，还有什么原因呢？企业有更多的人为控制。城市虽然有市长，但是城市相对更加自然，城市需要更多的人自主地选择，自主地租房子，自主地搬家，想走就走。所以，城市更接近于一个没人掌管的生命体。而企业如果老板自己的想法特别多，他总想这样做，总想那样做，总想管控所有，那么管理成本就会非常快地增加。我有一次到一个地方，他们给我介绍，说你看到这一栋楼吗，这是一个上市公司的楼。我说挺气派，他说整个这栋楼都是服务老板一个人的。就是老板一个人的服务班子，他的秘书、智囊就占一栋楼。我说这公司完了，因为如果一个公司的老板需要这么多人来服务他的话，这个公司熵增得有多严重，管理成本得有多高。当你的管理成本和损耗，以及你的错误决策多到一定程度的时候，你的生命所产生的回报就已经不能够养活这一切。

 

大家应该知道，更多的规则、官僚体系和生物体当中，更多的能耗是一样的，因为吸收的能量一部分用来生长，一部分用来维持。这也解释了为什么我们长到一定的阶段就不长了，我们的身体长到1米8基本不长了，为什么呢？能量进入体内一部分用来生长，一部分用来维持。当你那个维持的能量足够大，大到没有能量再分配给生长的时候，你就停止生长。所以当我们的身体大到一定程度的时候，我们的能耗其实增加了。这个时候，你会发现我们的成长曲线朝稳定走了。而我们的摄入能量又是有限的，你作为一个生命，就算靠吃获取能量，但不可能吃无限多。

 

这让我想起恐龙的灭绝，恐龙为什么会灭绝，其实就是因为恐龙当时已经太大了，因此当小行星撞击地球的时候，整个环境变得非常糟糕，长期被尘埃所埋着，太阳也照不进来，导致大量的生物死亡，但是老鼠活了下来，蜥蜴活了下来，跳蚤、蚊子、病毒都活了下来。为什么呢？因为人家能耗小，人家虽然寿命没有恐龙长，但是能耗小，所以它需要的边界条件更低，它就能够活下来。恐龙已经成了地球上的霸主，每天需要的能耗那么多，不能够再少，供给少了就受不了。所以企业也是一样，当企业大到一定的程度以后，比如现在有上百万人的企业，当有上百万人的企业出现了以后，你会发现这个企业对于外在环境的要求更高，它对于波动性的适应度更低。所以当环境产生大幅波动的时候，雷曼兄弟（美国第四大投行，2008年9月15日，宣布申请破产保护）这样的公司就率先倒闭了。

 

那讲到这儿，我们最后总结，最后一章叫作规模的极限。到底有没有一个规模的极限，这个规模的极限就是有限时间奇点，奇点来临。你说人的死亡是怎么回事，人的死亡就是生命走过了那个奇点，然后突然之间就死亡了。恐龙在无限增长的过程当中走到这儿，已经很危险了，那颗小行星一冲击，到了那个奇点，然后灭绝了。所以所有的这些随着规模的增长，我们都在不断地接近那个奇点。城市的奇点可能更远一点，因为城市更加自然，更加具有生命的特征。

 

那么这些规模不断扩大的城市、国家、生命是怎么维持下去的呢？靠的是范式转移。什么叫范式转移？假如人类是靠打猎活着的，根本养活不了这么多的人。所以第一个范式转移就是农业，我们发现了农业。然后假如我们都是靠农业要养活70亿人，那不可能，所以就有了工业。然后靠工业革命养活这么多人，现在也变得不可能，怎么办呢？我们要有IT、生物能源、太阳能这样的范式转移。你们有没有发现这个范式转移也符合这样一条幂次曲线，也就是说农业的范式转移大概花了20万年，然后到了这个工业革命以后，我们大概是以百年为单位，到了信息革命以后，我们可能是以十年为单位，到了现在我们大概就得以几年为单位进行范式转移。

 

所以我们踏上了一个规模所带来的停不下来的跑步机，这个跑步机会变得越来越快，对于创新的要求变得越来越高，我们得不断地完成新的范式转移，才能够保证我们这个越来越大规模的人类的总的生命体能够活下去。这就是这本书给我们最大的启发。很多读者会说为什么要听这么一本书呢，为什么要学一个大而无当的、跟我的生活没有关系的书？我认为恰恰相反，我觉得这本书跟我们的生活关系很大。就拿育儿来说，你说为什么我们对于孩子需要有耐心，因为孩子不是线性成长的，孩子是幂次成长的。为什么对于公司的管理，我们要讲究去官僚化，我们要尽量减少公司的熵增，要把权力下放到一线，因为生命体的规律就是这样，你越是把所有的能量都集中在头部，你距离那个奇点就越接近，我们需要更多地让这个生命变得灵活。把一个大象这样的机构变成蚁群这样的机构，那你的生存能力就会比大象强很多。