复旦大学在读博士：动态规划使用简明总结

你好，我是 zhenguo

今天很高兴为你推送一篇来自复旦大学在读博士 无尘 的关于动态规划的总结，话不多说，先睹为快。

从数学的视角来看，动态规划是一种运筹学方法，是在多轮决策过程中的最优方法。

那么，什么是多轮决策呢？其实多轮决策的每一轮都可以看作是一个子问题。从分治法的视角来看，每个子问题必须相互独立。但在多轮决策动态规划中，这个假设显然不成立，这是与分治法的明显不同之处，也是动态规划方法产生的原因之一。

动态规划是候选人参加面试的噩梦，也是面试过程中的难点。以下我根据自己的理解总结了动态规划相关的一些重要概念，便于从宏观上抽象理解这个算法。如果有不清楚的地方，非常欢迎大家留言讨论。

这是我绘制的动态规划知识点的一个思维导图：

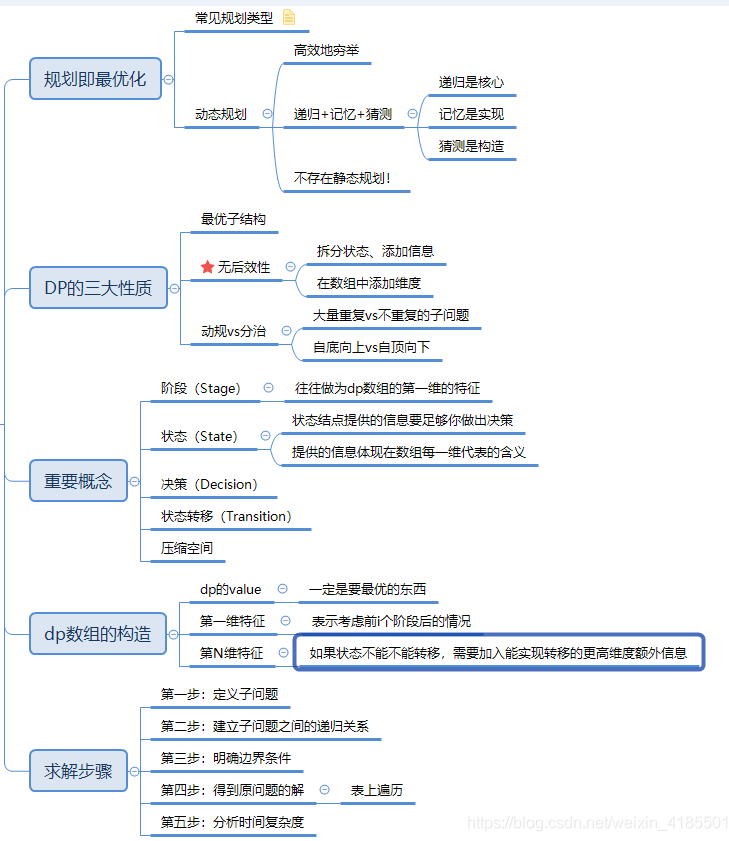
下面举一个例子：

题目

有若干硬币排成一个序列，面值依次为[5,1,2,10,6,2]，现在规定不能捡相邻的硬币，请问如果捡硬币才能使得捡到的硬币总价值最大。

思路

我们需要设计dp表来作为动态规划的数据模型，dp的值显然是硬币的总价值，表格的第一维是第几枚硬币，决策（也就是选择）有两个：

• 第一个是选择第i-1个硬币
• 第2个是不选择第i-1个硬币

这样我们就可以写出状态转移方程：

dp[i] = max(dp[i-2]+row_coins[i-1],dp[i-1])

注意我们还需要定义边界条件：

dp[0] = 0
dp[1] = row_coins[0]

这样我们就可以得到如下求解代码，最后编写traceback函数通过回溯来把选择的硬币打印出来。

代码

# 通过自底向上的方法来找到最优解
def bottom_up_coins(row_coins):
 dp = [None] * (len(row_coins)+1)
 dp[0] = 0
 dp[1] = row_coins[0]

 for i in range(2,len(row_coins)+1):
  dp[i] = max(dp[i-2]+row_coins[i-1],dp[i-1])

 return dp

c = [5,1,2,10,6,2]
dp = bottom_up_coins(c)

# 通过对dp的回溯来反向查找被选择的硬币
def trace_back_coins(c,dp):
 select = []
 i = len(c)
 while i>=1:
  if dp[i] > dp[i-1]:
   select.append(c[i-1])
   i -= 2
  else:
   i -= 1
 return select

print(dp)
print(trace_back_coins(c,dp))

运行结果

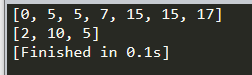
我们看到，用这种方法，很快能求得我们在选取 2、10、5这三枚硬币的时候，能得到最优的结果 17.

感谢无尘博士以上对动态规划的总结，若你意犹未尽，可以阅读学习为你准备的 Python 数据分析和算法 这本经典的电子书，微信备注：算法