原创 | 一文读懂无模型的预测(强化学习二)

作者:黄娘球
本文约2200字,建议阅读5分钟
本文讲述无模型的预测 (Model-free Prediction)通过与环境的交互迭代来求解问题。
上文(《原创 | 一文读懂强化学习在动态规划领域的应用》)回顾了强化学习的基础概念,以及预测与控制 (求解已知的MDP)。在已知的马尔可夫决策过程(MDP)中,无论是策略迭代(policy iteration)还是价值迭代(value iteration),都假定已知环境(Environment)的动态和奖励(dynamics and reward),然而在许多的真实世界的问题中,MDP模型或者是未知的,或者是已知的但计算太复杂。本文讲述无模型的预测与控制Model-free Prediction and Control 中的前半部分,无模型的预测 (Model-free Prediction)通过与环境的交互迭代来求解问题。
Lecture 3 无模型的预测与控制(Model-free Prediction and Control)
无模型的预测与控制,即在一个未知的马尔可夫决策过程(MDP)中,估计与优化价值函数。
3.1.无模型的预测(Model-free Prediction):
在不知道模型的情况下做策略评估,即如果我们不知道MDP模型,估计一个特定策略的期望回报。
3.1.1 蒙特卡洛策略评估(Monte-Carlo policy evaluation)
一、概述
a. 

b. 蒙特卡洛模拟(MC simulation):简单地采样大量的轨迹(Trajectories),使用经验平均回报,而不是期望回报。
c. 不要求MDP dynamics 或者奖励,没有 bootstrapping,也不假设状态是马尔可夫(Markov)的。
1. 评估状态s的价值函数 V(s):
a. 增量计数(Increment counter):
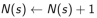
b. 增量总回报( Increment total return):
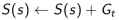
c. 价值由平均回报来估计:
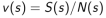
2. 由大数定律,有:
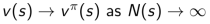
二、增量式蒙特卡洛更新 (Incremental MC Updates)
a. 各个回合的状态、动作和奖励集合:
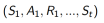
b. 每一个状态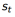
 及计算得到的回报
及计算得到的回报
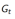

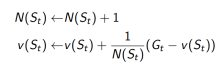
c. 或者在非平稳问题(non-stationary problem)上使用动态均值(running mean):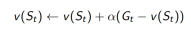
三、动态规划(DP)和蒙特卡洛 (MC)在策略评估上的不同
1. 动态规划DP通过bootstrapping计算
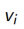 , 在贝尔曼期望方程上迭代
, 在贝尔曼期望方程上迭代

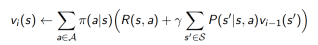
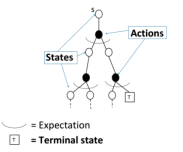
2. 蒙特卡洛MC在一个采样的回合中更新经验平均回报,来近似期望值。

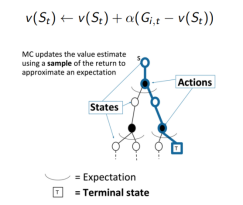
蒙特卡洛MC在以下情形优于动态规划DP:
a. 当环境是未知时,MC是有效的
b. 通过采样回合是由巨大优势的,即使是在已知环境的所有动态,例如当转移概率矩阵太复杂而难以计算的时候。
3.1.2 时间差分(Temporal Difference, TD)
TD通过bootstrapping从不完整的回合中学习,无模型(Model-free)直接从经验的回合中学习。
目标:在策略π下通过经验学习
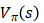
TD (0) :
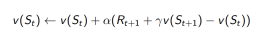
TD target: 
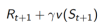
TD error:
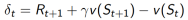
对于任何的固定策略π ,TD (0) 已被证明收敛于
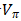
一、时间差分TD优于蒙特卡洛MC的情形
1. TD通过bootstrapping来更新价值估计,使用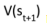
 的估计来近似期望值。
的估计来近似期望值。
2. MC 使用采样的回报
二、TD和MC的对比
1. TD可以在每一步在线学习,而MC必须等到回合结束才知道回报。
2. TD可以从不完整的序列sequences学习,MC只能从完整的序列中学习
3. TD在连续continuing(非终止non-terminating)环境下有效,MC只在回合制episodic(终止terminating)环境下有效
4. TD应用了马尔可夫性质(Markov property),在马尔可夫环境下(Markov environment)更有效。而MC并没有应用马尔可夫性质,在非马尔可夫环境下更有效。
三、n步TD(n-step TD)
1. 考虑下面的n-step returns

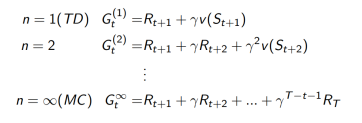
2. n步回报

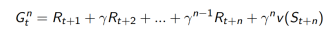
3. n步TD

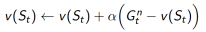
四、
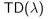
n步回报的平均
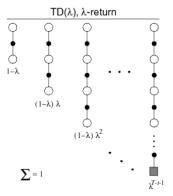
1. 
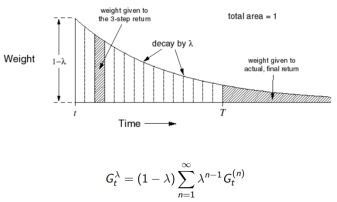
 以权重
以权重
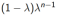 结合了所有的n步回报
结合了所有的n步回报
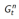

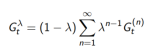
2. 前向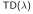 (
(
 )
)

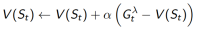
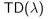
 的权重函数
的权重函数

前向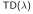

1. 向着
 更新价值函数
更新价值函数
2. 前向,即向前看未来以计算

3. 像MC一样,只能在完整的回合里计算
后向
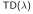
每一步都从不完整的序列sequences在线更新
1. 每一状态s都保持一个Eligibility Traces

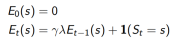
2. 为每一个状态s更新价值V(s)
3. 与
 成比例
成比例

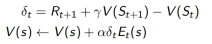
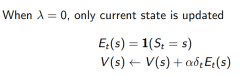
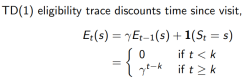
TD(1) 几乎等价于every-visit Monte-Carlo
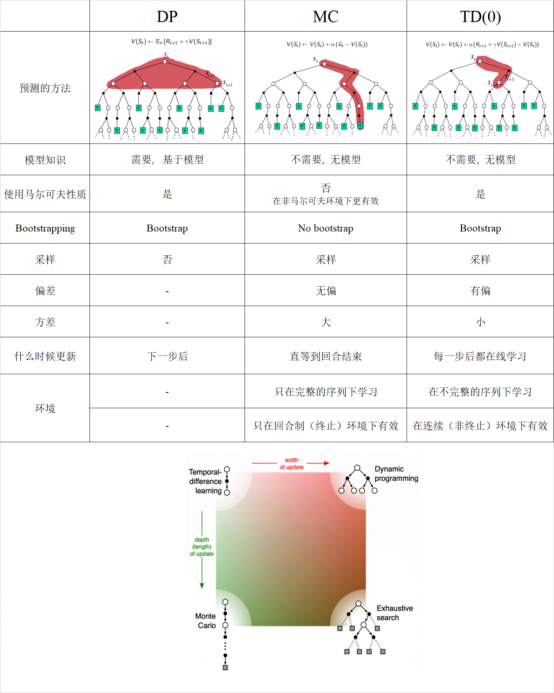
3.1.3 总结

编辑:于腾凯
校对:林亦霖
作者简介
黄娘球,广东财经大学统计与数学学院,21级统计学硕士研究生,一个对AI各领域有广泛兴趣的技术狂热者,感兴趣的领域包括:Explainable AI,AI Safety and Alignment,AIGC, LLMs。读研前曾是广东以色列理工学院GTIIT(以色列理工学院(Technion, Israel)中国校区)的Staff。目前是数据派THU研究组志愿者,AI TIME学术部志愿者。且在安远AI担任线上作者,职责包括帮助修改、审核文章,提供AI Safety and Alignment领域内的原创稿件。主持2022年广东省科技创新战略专项资金(攀登计划)资助项目,可解释神经网络赋能政府统计工作的可行性研究。乐于分享交流,思想碰撞。始终保持高度的学习热情,享受潜心科研的过程。
数据派研究部介绍
数据派研究部成立于2017年初,以兴趣为核心划分多个组别,各组既遵循研究部整体的知识分享和实践项目规划,又各具特色:
算法模型组:积极组队参加kaggle等比赛,原创手把手教系列文章;
调研分析组:通过专访等方式调研大数据的应用,探索数据产品之美;
系统平台组:追踪大数据&人工智能系统平台技术前沿,对话专家;
自然语言处理组:重于实践,积极参加比赛及策划各类文本分析项目;
制造业大数据组:秉工业强国之梦,产学研政结合,挖掘数据价值;
数据可视化组:将信息与艺术融合,探索数据之美,学用可视化讲故事;
网络爬虫组:爬取网络信息,配合其他各组开发创意项目。
点击文末“阅读原文”,报名数据派研究部志愿者,总有一组适合你~
转载须知
如需转载,请在开篇显著位置注明作者和出处(转自:数据派THUID:DatapiTHU),并在文章结尾放置数据派醒目二维码。有原创标识文章,请发送【文章名称-待授权公众号名称及ID】至联系邮箱,申请白名单授权并按要求编辑。
未经许可的转载以及改编者,我们将依法追究其法律责任。
点击“阅读原文”加入组织~

